三步式电磁馈能减振器参数匹配方法*

崔丹丹 苟春梅 吴 民

（新疆交通职业技术学院汽车工程分院 新疆 乌鲁木齐 831401）

引言

汽车在行驶过程中，会由路面不平引起悬架振动，传统减振器将这部分振动能量转换为热能消耗掉。本文研究的滚珠丝杠式电磁馈能减振器，由滚珠丝杠与馈能电机组成，在产生电磁阻力矩的同时，提供悬架所需的阻尼力，可将振动能量转化为电能储存或加以利用。由于受馈能电机的最大转矩-转速特性限制，馈能减振器表现为分段的非线性阻尼特性。因此，馈能电机参数的选择尤为重要。在过去的20年间，学者们对馈能减振器的结构[1]、回收能量的潜力[2]、主动及半主动控制算法[3]等进行了深入研究，但有关馈能减振器的参数选择更多是依赖于经验，没有一种完整的匹配方法。相比于传统减振器，馈能减振器在工作过程中，有滚珠丝杠和馈能电机等部件的旋转运动。因此，馈能减振器不仅输出阻尼力，还产生惯性力。有些文献提到了惯性力的存在，但很少对其进行深入研究。因此，本文首先分析了馈能减振器的惯性力和阻尼特性对车辆平顺性和操作稳定性的影响。在此基础上，采用遗传算法找到最优值，确定馈能电机线性阻尼区间的阻尼系数。使用概率统计法确定馈能减振器阻尼特性中的恒阻尼力。结合实际，由传统电机的基速比确定馈能减振器的阻尼衰减区间特性，从而得到馈能电机额定功率等重要参数，并确定馈能电机的型号。最后，通过仿真验证这种方法的有效性。

1 二自由度车辆振动模型

在研究车辆垂直方向的运动时，二自由度车辆振动模型能够反映车身和车轮的动态特性，并对车辆的平顺性和安全性进行有效分析。

1.1 馈能减振器的结构

本文研究的是滚珠丝杠式馈能减振器[4]，其结构如图1所示。图1中，Z和F下方箭头的方向为位移Z和阻尼力F的传递方向。

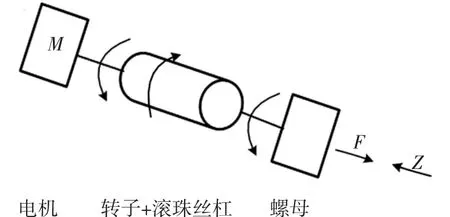
图1 馈能减振器结构示意图

1.2 含有馈能减振器的二自由度车辆振动模型

馈能减振器中的馈能电机和滚珠丝杠在运行过程中会产生与转动惯量成正比的惯性力，惯性力的大小与馈能减振器的相对运动加（减）速度相关。将惯性力等效为馈能减振器的惯性质量mr，馈能电机的阻尼特性用cr表示[5]。在传统的二自由度车辆振动模型中引入馈能减振器，含有馈能减振器的二自由度车辆振动模型[6]如图2所示。

根据图2所示的模型，建立含有馈能减振器的二自由度车辆振动方程如下：

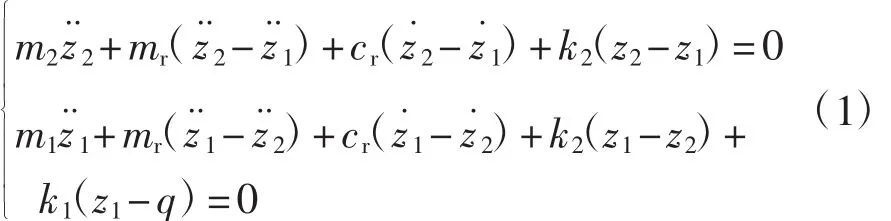
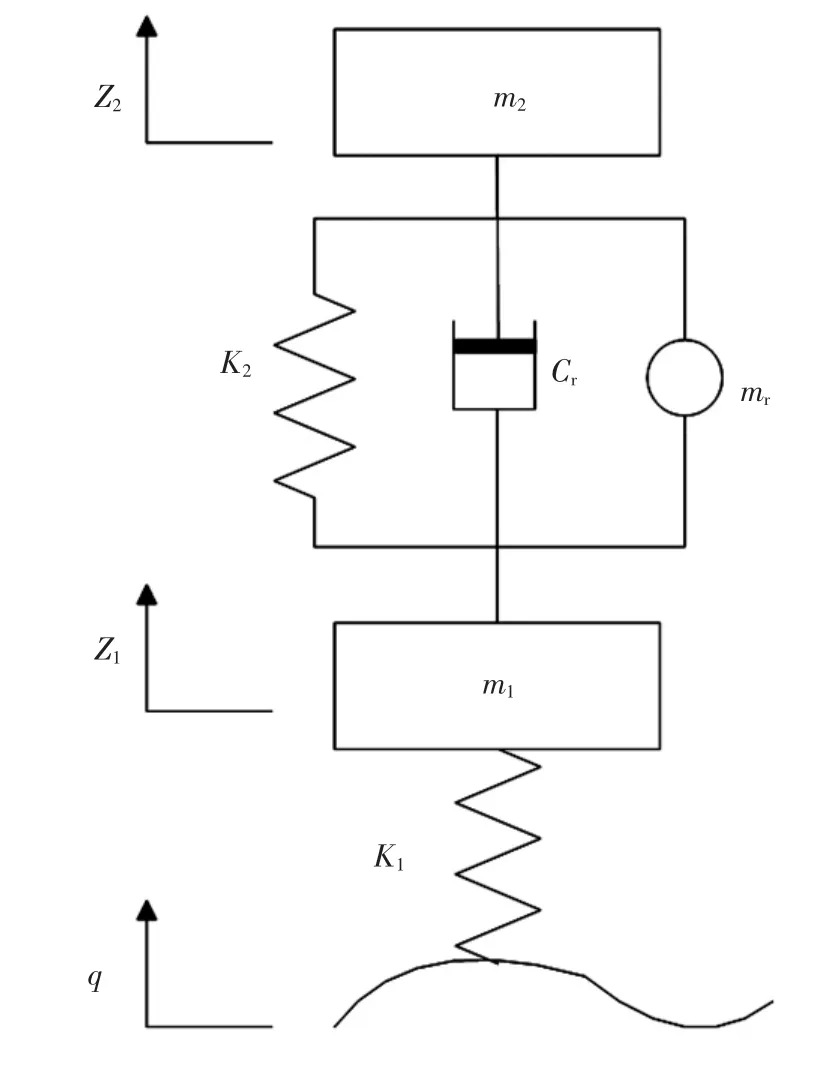
图2 含有馈能减振器的二自由度车辆振动模型

式中：m1为非簧载质量，kg；m2为簧载质量，kg；mr为馈能减振器的惯性质量，kg；k1为轮胎刚度，N/m；k2为悬架弹簧刚度，N/m；q为路面垂直位移，m；z1为车轮垂直位移，m；z2为车身垂直位移，m。

根据此数学模型建立Simulink仿真模型时，路面输入采用滤波白噪声激励[7]，使仿真工况更接近实际。

2 馈能减振器对车辆性能的影响

馈能减振器与传统减振器的区别在于含有做旋转运动的馈能电机转子和滚珠丝杠，若馈能电机转子的质量较大或悬架运动加速度过高，惯性力会很大，因此在为馈能减振器匹配馈能电机时，应考虑馈能减振器的惯性质量对车辆性能的影响[8]，馈能电机所能提供的阻尼特性受到馈能电机最大转矩-转速特性的限制，这是影响车辆性能的重要因素。因此，在选择馈能电机参数时，需首先分析馈能减振器的惯性质量和馈能电机所能提供的阻尼特性对车辆性能的影响。

2.1 评价车辆性能的指标

振动响应量包括车身加速度z¨2、车轮动载荷Fd、悬架动挠度fd等，分别为评价车辆平顺性、操作稳定性和舒适性的指标。每个振动响应量的均值近似为零，因此取每个振动响应量的均方根值作为评价指标[9]。

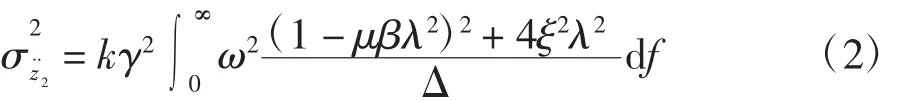
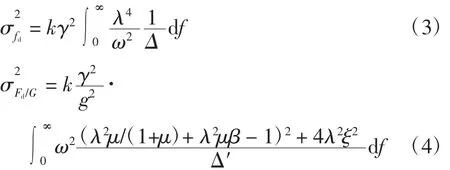
式中：质量比μ=m1/m2；刚度比γ=k1/k2；馈能减振器的惯性质量与车轮质量的比值β=mr/m1；固有频率比λ=ω/ω0；路面速度功率谱密度k=4π2Gq（n0）n20u，0.1 m3/s。Δ与Δ′的表达式分别为：

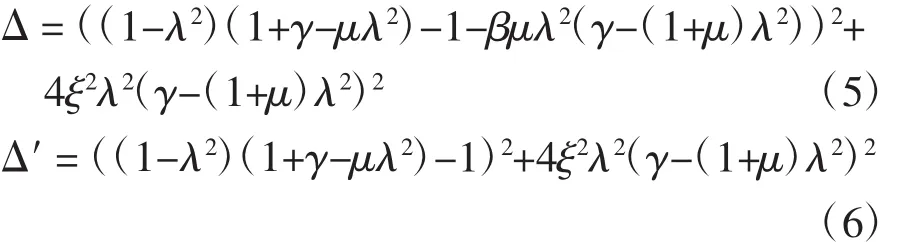
如果仿真结果中各振动响应量均方根值的±3倍均小于1，则说明车辆行驶时安全性好。假设车轮相对动载荷均方根值的±3倍超过1，则Fd/G的值大于1的概率p为0.3%，车轮跳离地面即车辆失去控制的概率（1-p）很大，说明车辆行驶时安全性较差。如表1所示。

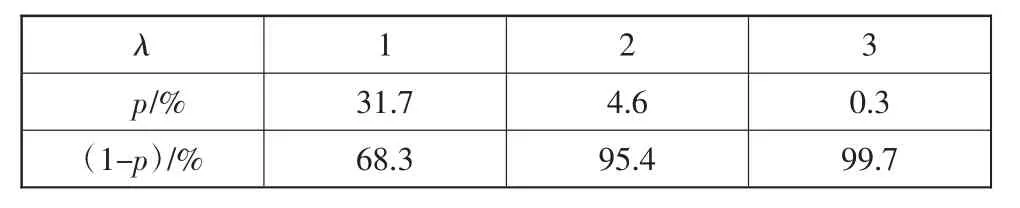
表1 正态分布的概率密度表

2.2 馈能减振器的惯性质量对车辆性能的影响

由于馈能减振器的惯性质量和阻尼特性在影响车辆性能的因素中所占比重较大，重叠分析会产生混淆，因此，分析馈能减振器的惯性质量对车辆性能的影响时，假定馈能减振器的阻尼特性与传统减振器的阻尼特性相同。

2.2.1 频域内的分析

以β=0时传统减振器悬架的振动响应量的均方根值作为基准，分别将公式（2）、公式（3）、公式（4）中馈能减振器的惯性质量增加和减小一定的值，其他参数保持不变（当车轮质量m1不变时，改变β相当于增加或减小馈能减振器的惯性质量mr的值），观察馈能减振器的惯性质量对各个性能指标的影响。计算结果如图3所示。

从图3可以看出，馈能减振器的惯性质量主要是对车身加速度的均方根值和车轮相对动载荷的均方根值有影响均随β的增加而增加，说明馈能减振器的惯性质量会对车辆行驶的平顺性和操作稳定性带来不利影响，随着馈能减振器的惯性质量增大，产生的不利影响越明显。

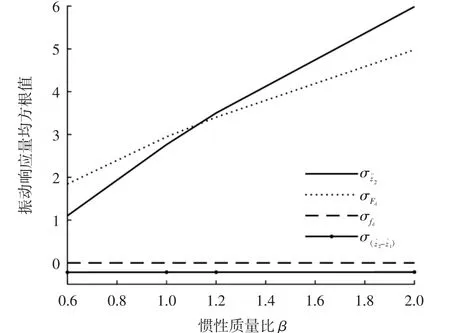
图3 惯性质量比β对振动响应量均方根值的影响图

2.2.2 时域内的分析

根据公式（1）建立含有馈能减震器的二自由度车辆振动模型的Simulink模型，在时域内对Simulink模型的性能进行仿真。经过分析可知，馈能减振器的惯性质量的表达式为：

式中：Jm为馈能电机的转动惯量，kg·m2；Jb为滚珠丝杠的转动惯量，kg·m2；l为滚珠丝杠的导程，mm。

从公式（7）可以看出，馈能减振器的惯性质量与滚珠丝杠的导程、馈能电机及滚珠丝杠的转动惯量等有关。仿真时，只改变馈能减振器的惯性质量，车辆其他参数不变。表2为时域内馈能减振器的惯性质量对车辆各个性能指标的影响。

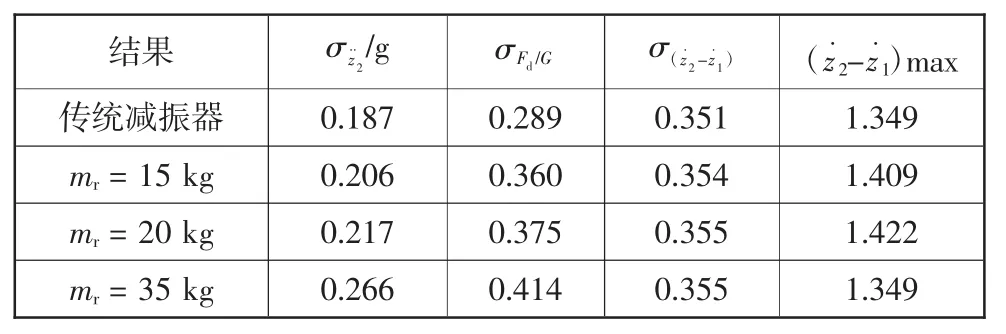
表2 馈能减振器的惯性质量对车辆性能的影响

从表2和图3可以看出，随着馈能减振器的惯性质量增大，车身加速度的均方根值增大，表明车辆平顺性变差；车轮相对动载荷的均方根值逐渐增大，表明操作稳定性变差；而馈能减振器的惯性质量对相对运动速度的均方根值 σ（z˙2-z˙1）影响不大。与频域分析中馈能减振器的惯性质量对各性能指标的影响进行对比，可以看出，两者的变化趋势相同。馈能减振器悬架系统中特有的惯性质量对车辆的振动特性产生明显的不利影响，应当减小惯性质量。

2.3 阻尼特性对车辆性能的影响

馈能减振器作为阻尼元件，其所能提供的最大阻尼如图4所示。

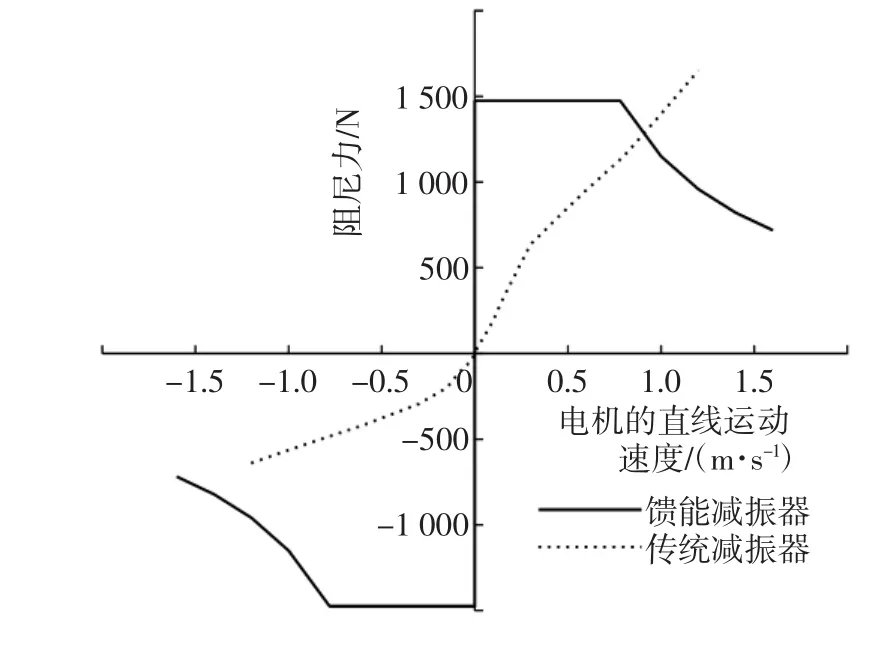
图4 传统减振器与馈能减振器阻尼特性对比图

从图4可以看出，传统减振器的线性阻尼特性和馈能减振器的阻尼特性差别很大。馈能电机在初始阶段为恒阻尼力区，当其进入恒功率区间后，馈能电机输出的功率是一定的，但所能提供的阻尼力逐渐减小，而传统减振器的阻尼力随着馈能电机直线运动速度的增加而不断增加。

为了用馈能减振器替代传统减振器，最简单的办法是选用更大转矩/功率的馈能电机，使馈能减振器的最大阻尼力-速度曲线完全覆盖对应的传统减振器的阻尼特性曲线，然后通过对馈能电机的转矩进行控制以达到同样的阻尼特性。然而，这种方法既不可行也不经济。馈能减振器为非簧载器件，其安装空间非常有限，增大馈能电机的功率/转矩，会使其质量和转子的转动惯量都增大，使悬架性能恶化。而且，较大的体积也制约了其使用范围。另一方面，这种情况下，馈能电机在大多数时间都工作于非常小的负载之下，造成浪费。

所以，可行的方法是使馈能减振器的最大阻尼-速度特性部分覆盖对应的传统减振器的阻尼特性，使馈能减振器所匹配悬架的特性保持在可接受的范围内。另外，因为馈能减振器在低速阶段的阻尼力为恒定值，因此需要对馈能电机进行控制，变为线性阻尼特性。结合馈能电机高速阶段（馈能电机的直线运动速度较高的阶段，图5中超过0.8 m/s的速度范围），所得到的馈能减振器的阻尼特性为分段的非线性阻尼特性，由线性阻尼区、恒阻尼区和阻尼衰减区组成[10]，如图5所示，图中v0表示恒阻尼力区对应的临界速度，vdecr表示阻尼衰减区对应的临界速度。

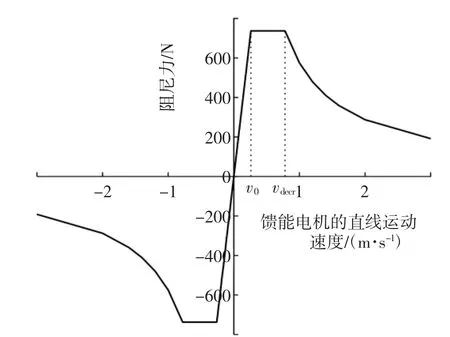
图5 馈能减振器非线性阻尼特性

3 三步式电磁馈能减振器参数的匹配

车辆参数如表3所示，从表3可以得到仿真所需的各个参数。

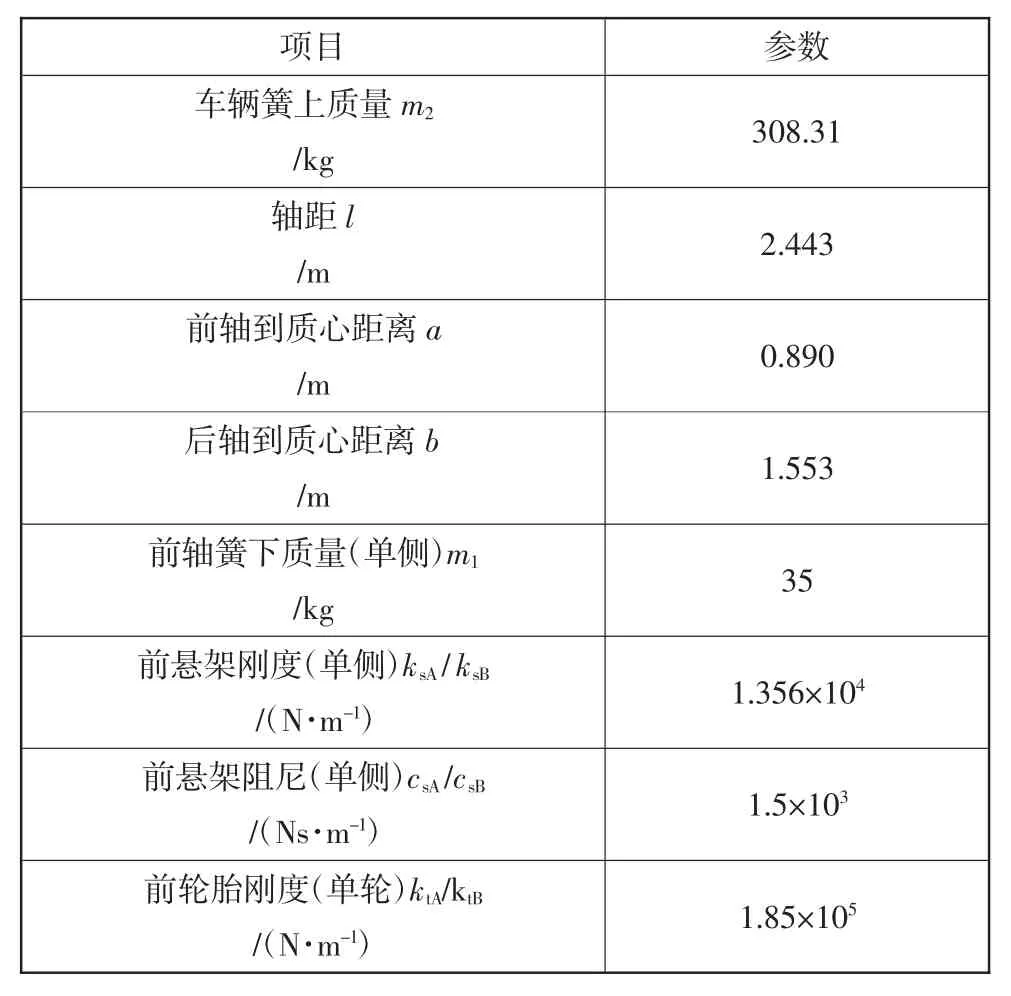
表3 车辆参数表

仿真时，随着路面不平度和车速的增加，车辆振动响应量增加，车辆的各项性能指标在极限工况下较难控制。因此，本文分析的路面工况定为D级，车速定为10 m/s。

三步式电磁馈能减振器参数的匹配流程如图6所示。

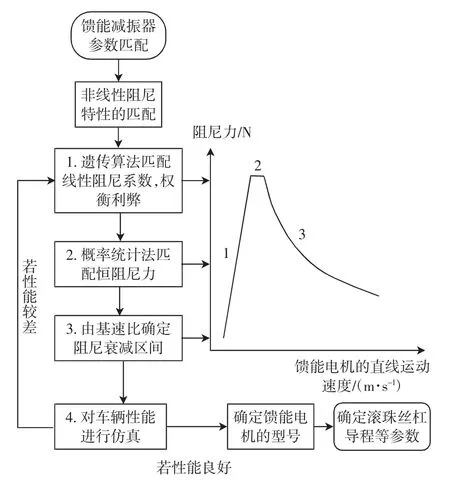
图6 三步式电磁馈能减振器参数匹配流程图

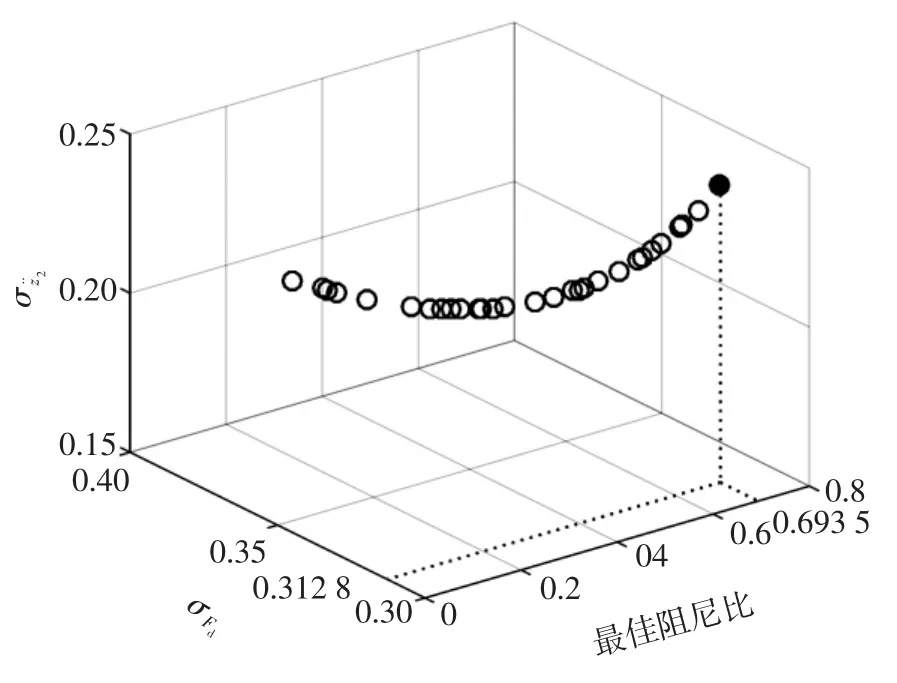
图7 多目标Pareto前沿图

表4 阻尼系数对各响应量均方根值的影响

在匹配三步式电磁馈能减振器的参数时，首先匹配馈能电机的阻尼特性，不同的阻尼特性对应不同的馈能电机参数。由之前的分析可知，用馈能减振器代替传统的减振器时，引入的惯性质量会使车辆各个性能指标都变差，由车轮相对动载荷的均方根值可以看出，车轮跳离地面的概率很大。根据图4，若是馈能电机的阻尼特性满足传统减振器的需求，悬架最大相对运动速度为1.2 m/s，对应的阻尼力为1 651 N。经过计算，馈能电机的功率为2 kW，显然，功率过大，不利于馈能减振器的经济性和实用性。因此，不能直接用传统减振器的阻尼系数匹配馈能电机的线性阻尼区。通过优化计算可知，在减小馈能电机功率的同时，改善馈能电机的阻尼特性，从而改善车辆的性能。

3.1 遗传算法匹配线性阻尼区

根据传统减振器的性能可知，为获得较好的车辆平顺性，需要较小的系统阻尼；为获得较好的操作稳定性，则需要较大的系统阻尼。平顺性与操作稳定性的矛盾主要通过车辆阻尼参数体现出来。这是一个多目标优化的问题，为解决此类不同目标函数间的性能矛盾，本文采用基于NSGA-II改进的一种多目标优化算法[11]，结合本文问题描述，控制算法表示如下：

式中：f1、f2均为目标函数分别代表平顺性和操作稳定性。

假设馈能减振器为线性阻尼特性，约束条件将馈能减振器的阻尼系数c的范围限制在0～5000N（/m·s）。经过上述算法后，得到一组阻尼比以及对应的目标函数值，如图7所示。

由于仿真时所用的路面为D级，操作稳定性更不好控制，因此，选择使车轮动载荷均方根值相对较小的一组解作为计算数据，也就是ξ=0.693 5，根据阻尼比的计算公式求得阻尼系数c=2 836。表4为优化前后的仿真结果对比。

从表4可知，引入馈能减振器后，车身加速度的均方根值略微增大，但在合理范围内；车轮相对动载荷的均方根值大幅减小，达到安全范围。因此，遗传算法效果较好。

3.2 概率统计法匹配恒阻尼力

通过概率统计法匹配馈能电机非线性阻尼区的恒阻尼力。以D级路面的情况来看，传统减振器相对运动速度的均方根值 σ（z˙2-z˙1）为 0.26 m/s，λ =1 时，从表2可知，馈能减振器相对运动速度位于-0.26～0.26 m/s的概率为68.3%；λ=2时，馈能减振器相对运动速度位于-0.52～0.52 m/s的概率为95.4%。若取恒阻尼力对应的临界速度 v0为 σ（z˙2-z˙1），对应的恒阻尼力为 737N；若取 v0=2σ（z˙2-z˙1），对应的恒阻尼力为1 474 N。此时，在 D 级路面下，首先将 3σ（z˙2-z˙1）作为阻尼力衰减对应的临界速度vdecr。然后，将馈能减振器的最大测试速度1.6 m/s作为最大速度，不同v0的值所对应的2种阻尼特性如图8所示。

对上述2种馈能减振器的阻尼特性进行仿真，结果如表5所示。馈能减振器的惯性质量假定为20 kg。

对比表5中的2组数据，当恒阻尼力为737 N时，车轮相对动载荷的均方根值过大，以至于车辆行驶安全性较差，悬架相对运动速度的最大值也很大，不能满足安全需求。这是由于馈能减振器非线性阻尼进入恒阻尼力区间过早，所能提供的阻尼力不足所致。当恒阻尼力为1 474 N时，车辆行驶的平顺性和安全性都能得到保证。因此，恒阻尼力定为1 474N。利用概率统计的方法，用 2σ（z˙2-z˙1）和 3σ（z˙2-z˙1）分别作为v0以及vdecr来匹配馈能减振器悬架的非线性阻尼特性是有效的。

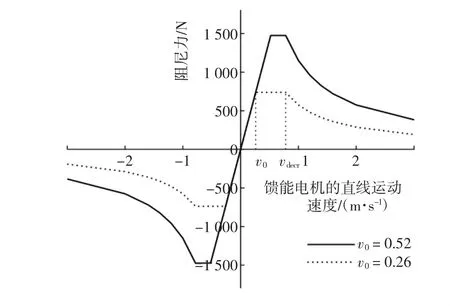
图8 馈能减振器非线性阻尼特性图

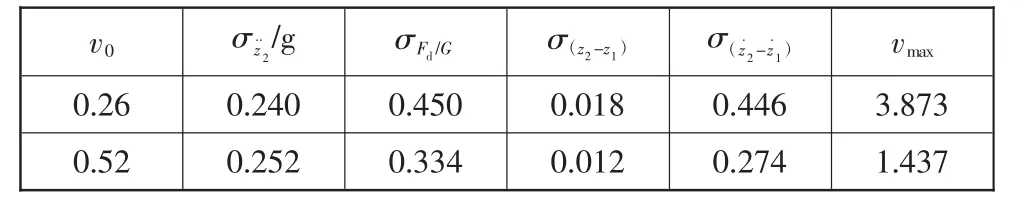
表5 不同临界速度对车辆性能的影响

3.3 阻尼衰减区的匹配

上述匹配出的非线性阻尼特性需与馈能电机本身的特性配合使用，阻尼力衰减区所对应的临界速度根据传统电机的基速比（最高转速与额定转速的比值）确定。传统电机基速比的对比如图9所示。

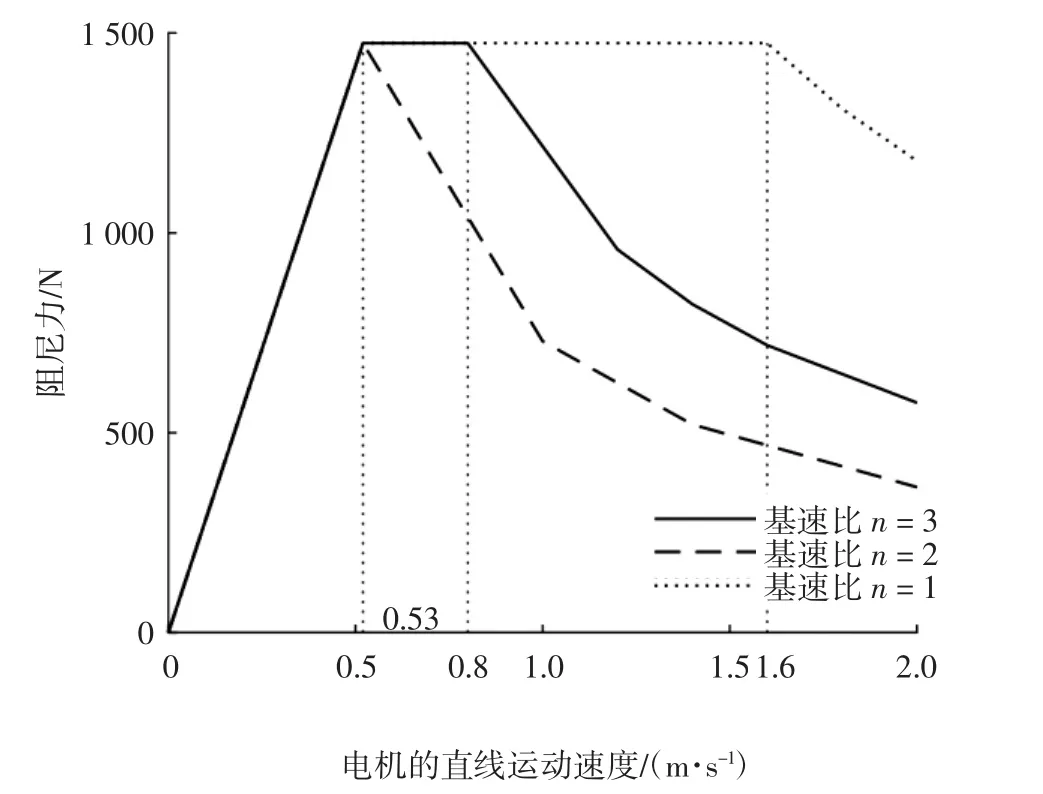
图9 传统电机不同基速比对比图

从图9可以看出，当基速比为1时，没有阻尼衰减区间，额定速度为最大速度，此时计算出的馈能电机功率过大不适用。当基速比为2时，额定速度为0.8 m/s，与非线性阻尼特性所定的vdecr接近。由之前的分析可知，此数据满足要求。当基速比为3时，恒阻尼力区间过小，不能满足要求。因此，取基速比为2。

3.4 馈能减振器参数的确定

结合上述分析，馈能电机的阻尼特性如图10所示。

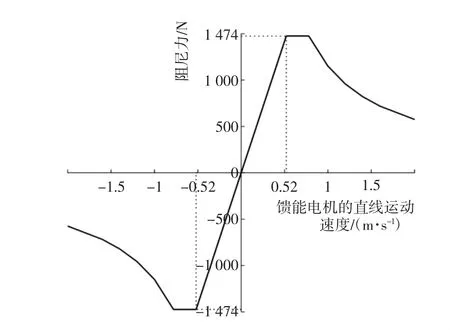
图10 馈能电机的阻尼特性

假定馈能电机的最高转速nmax为6 000 r/min，对应的馈能减振器悬架的直线运动速度为1.6 m/s，馈能减振器悬架的直线运动速度与馈能电机转速的关系式如下[12]：

式中：l为滚珠丝杠导程，mm。

由公式（9）可以求得滚珠丝杠的导程为16 mm，馈能电机转矩T和阻尼力F之间的关系为：

已知馈能电机的功率p和转速n，可近似得到不同基速比下的馈能电机转速n和转矩T的关系为：

通过公式（9）、公式（10）、公式（11）可求出馈能电机的额定功率和转矩。将馈能电机数据带入模型中，所得到的仿真结果如表6所示。

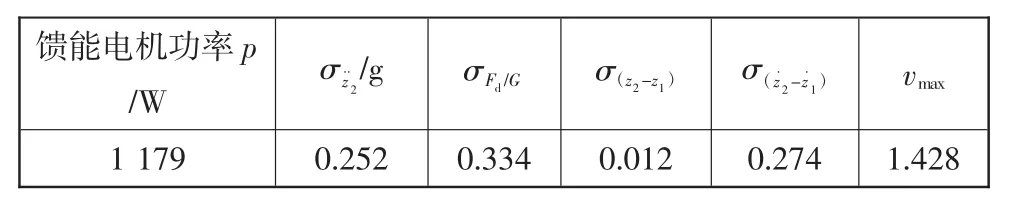
表6 馈能电机的确定

从表6可以看出，选择功率为1 179 W的馈能电机组成的馈能减振器，各项性能满足匹配要求。图11为馈能电机的外特性图。

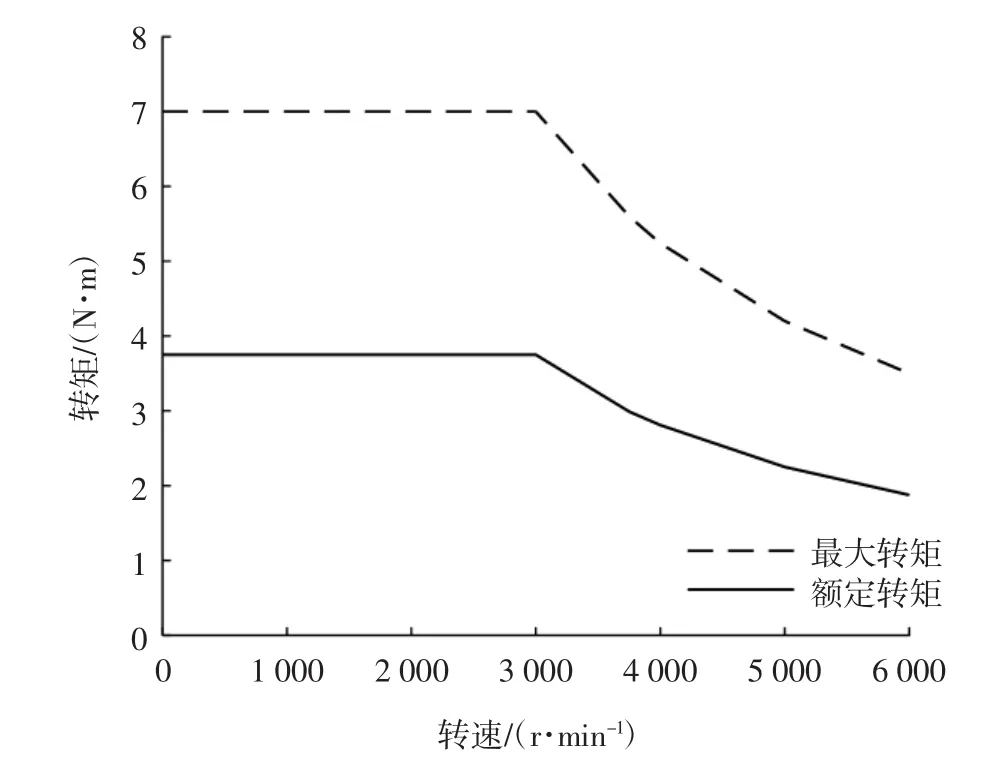
图11 馈能电机外特性图

本文所阐述的匹配方法主要针对极限工况，但在路面状况较好时仍然适用。

4 结论

本文提出了一种适用于电磁馈能减振器的参数匹配方法。建立仿真模型时，考虑了惯性力对车辆性能的影响，使仿真模型更加合理。匹配馈能减振器参数时，首先匹配馈能电机的阻尼特性，利用遗传算法寻找最优阻尼系数，作为馈能电机线性阻尼区的阻尼系数，解决了因参数复杂而造成的各个评价指标互相矛盾的问题。在此基础上，利用概率统计法结合传统电机基速比，得到馈能电机的恒阻尼力区间和阻尼衰减区间，最终确定馈能电机的非线性阻尼特性，从而确定馈能电机的额定功率以及滚珠丝杠导程等参数。对极限工况下的车辆性能进行仿真，结果表明，车辆的各个性能指标都在合理范围内，证明馈能减振器参数的匹配结果合理。