基于D-最优试验设计的麦弗逊悬架优化
2018-10-30周军超廖映华汤爱华
周军超,袁 杰,廖映华,汤爱华
(1.四川理工学院 机械工程学院,四川 自贡 643000; 2.人工智能四川省重点实验室,四川 自贡 643000)
麦弗逊式悬架具有结构简单、紧凑、占用空间少、性能优越等特点,同时还具有较为合理的运动特性,以保证整车性能要求[1].因此,麦弗逊悬架在前置前驱的乘用车上具有广泛的应用.
汽车的操纵稳定性影响车辆性能,而汽车出现故障频率较高的是车轮定位参数异常[2],尤其是车轮外倾角与前束的匹配不当会使车轮相对地面发生侧滑,加剧轮胎的磨损,影响汽车安全稳定性.近年来,Lee等[3-4]基于ADAMS/CAR模块、整车操纵稳定性及CARSIM参数化仿真技术,对汽车操纵稳定性进行了优化分析.Yao等[5-7]应用有限元方法进行结构优化设计,并进行了实验验证,可以显著降低悬架侧载.魏天等[8-10]对影响汽车平顺性的主要参数K&C进行了理论分析,为研究车辆整体性能和进一步了解悬架非线性特性的时域性提供思路.
随着计算机仿真技术的发展,运用虚拟样机平台和D-最优试验设计相结合对悬架参数进行优化.在设置重复试验的前提下,实验效率最高,将会在设计优化阶段节约很多时间和成本.
1 麦弗逊式悬架建模
整车参数如表1所示.
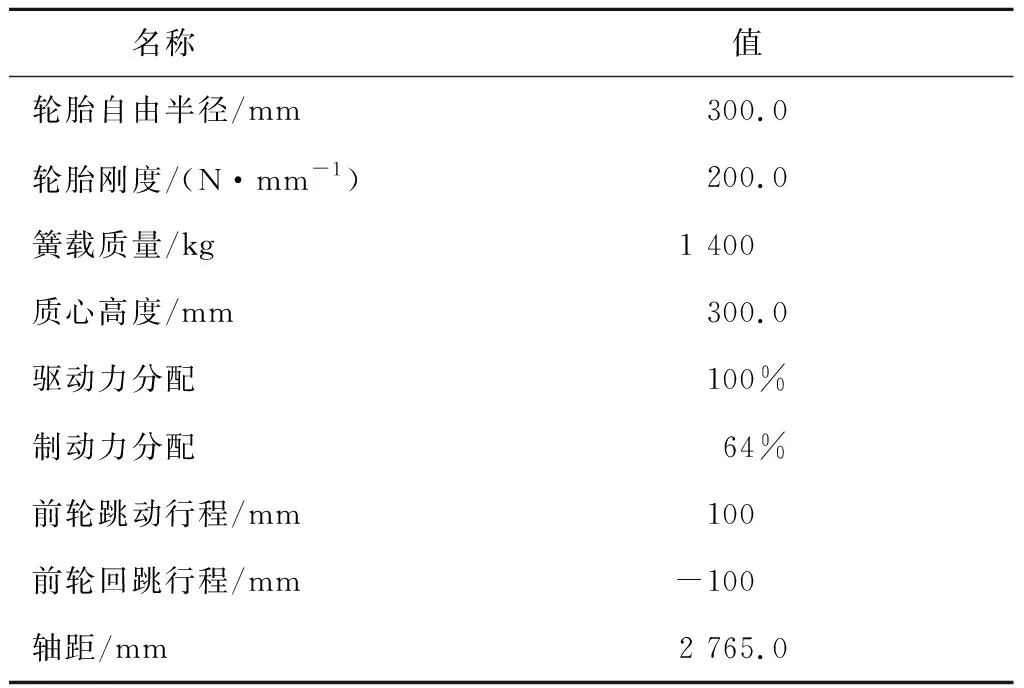
表1 悬架参数Tab.1 Suspension parameters
利用ADAMS/Car模块建立了麦弗逊式悬架的仿真模型[11-12],麦弗逊式悬架铰链类型与数目,以及机械体统的自由度DOF如下:
∑Rk
(1)
式中:n为活动构件总数;pi为第i个运动副的约束条件数;qj为第j个原动机的约束条件数;Rk为其他的约束条件.
麦弗逊式悬架悬架系统的自由度:DOF=6×14-m=3,分别是左右悬架的上下摆动、左右车轮绕车轴的转动和车轮绕主销的转动.在ADAMS/Car模块中建立麦弗逊悬架模型如图1所示.
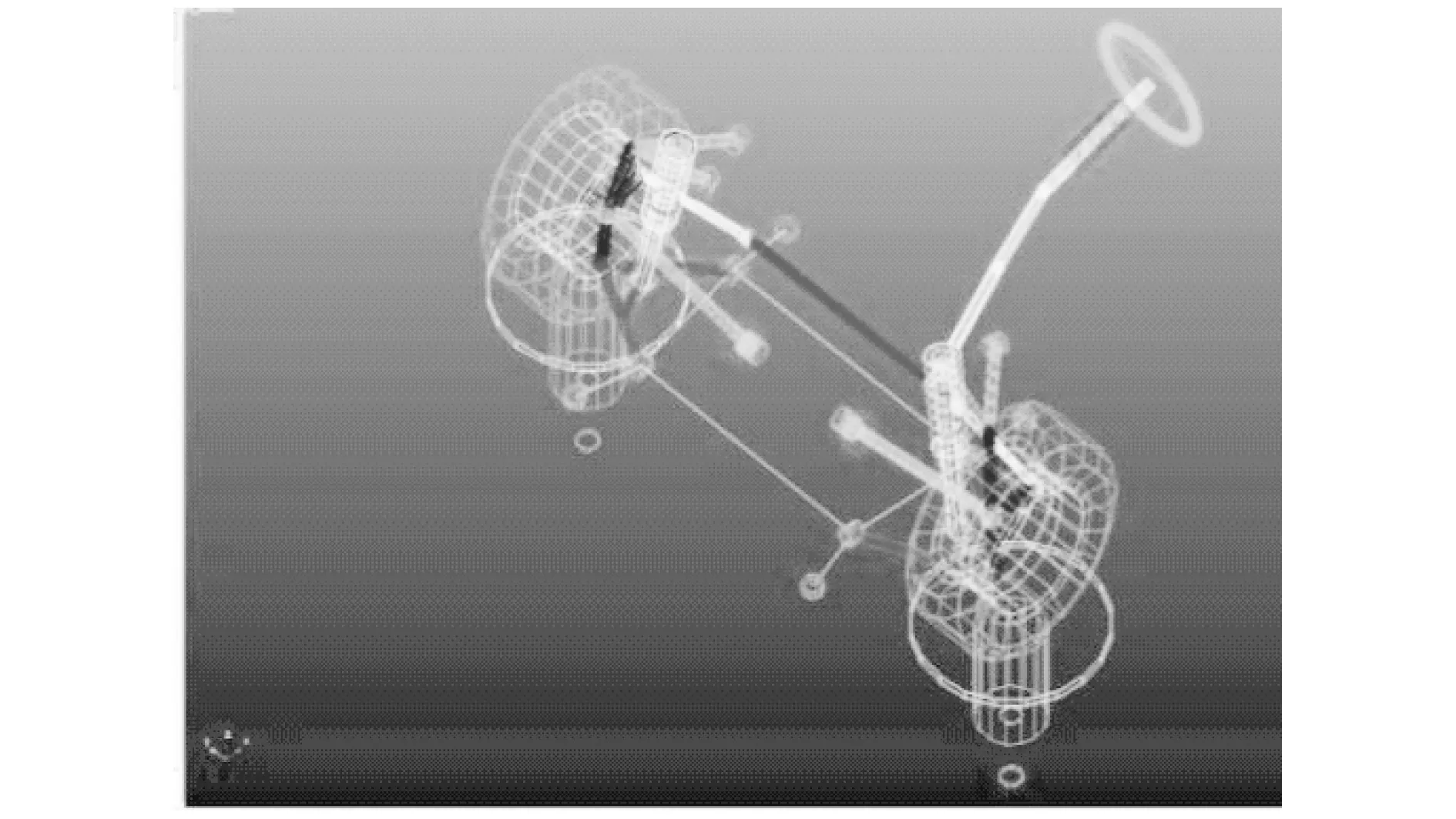
图1 麦弗逊式悬架模型Fig.1 McPherson suspension model
采用Adams/Car Ride提供的基于Sayers数字模型的路面属性文件,它是一种综合了许多不同类型道路测量参数,并给出了左、右轮辙路面轮廓参数的经验模型模型.模型认为路面轮廓的空间功率谱密度Ga和空间频率n存在如下函数关系:
(2)
式中:Ge为空间功率谱密度幅值;Gs为速度功率谱密度幅值;Ga为加速度功率谱密度幅值.
2 D-最优试验设计理论
设计研究是只有一个设计变量产生变化,而试验法设计是研究多个设计变量产生变化,且将多个设计变量的取值组成组,研究在设计变量取不同的可能组合是目标函数取值的情况,并且能够大幅度减少试验次数,且不会降低试验可行度[13].
首先需要选择试验因素水平相对应的正交表,然后根据约束条件及轿车设计经验,为设计变量(x1,x2,x3,x4)设定一定变化范围.试验因素(z1,z2,z3,z4)的变化范围与设计变量(x1,x2,x3,x4)有一定的转换公式[13].若令z1,z2,z3,z4,Δj和xj分别为第j个因素的上水平、下水平、零水平、变化区间和编码因素,则有下列公式成立:
3 麦弗逊式悬架D-最优试验设计
应用ADAMS/Car建立该车的前悬架仿真模型,并以目标样车前轮前束角、前轮外倾角、轮距和轴距随轮跳的变化等K&C特性曲线的斜率为目标,以(z1,z2,z3,z4)表示,并设置一定变量范围,则可以选取因素编码表[14].最后在ADAMS模块中,对该前悬架硬点进行整体灵敏度分析.根据灵敏度分析结果,选择对前轮磨损程度影响较大的前束角、外倾角以及轮距和轴距等参数为设计目标,进行水平互相匹配试验,选取较为灵敏的硬点进行优化.
具体优化方法:确定目标函数、设计变量和约束条件后,采用D-最优试验设计对悬架参数进行优化,流程如图2所示.
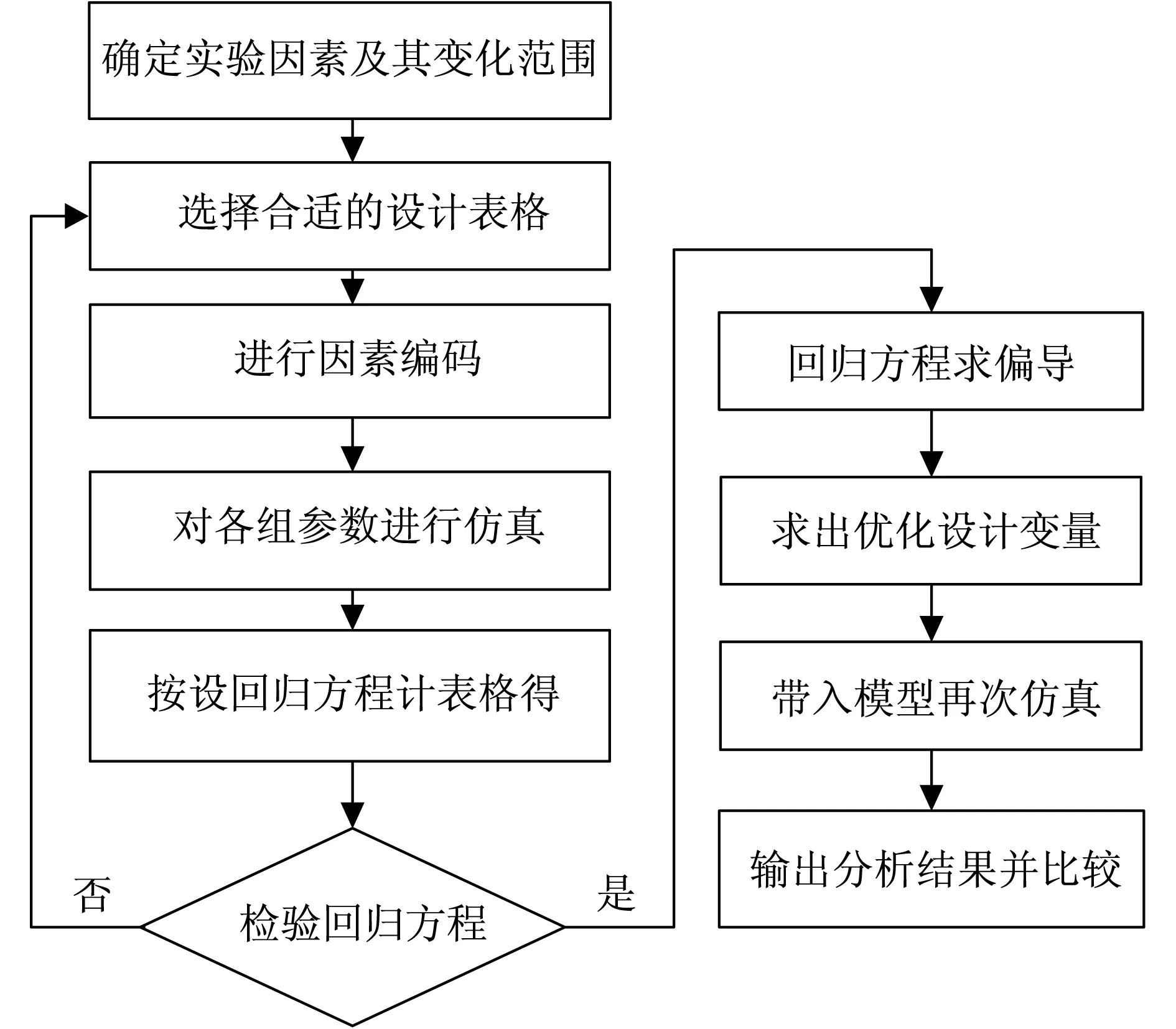
图2 D-最优试验设计流程图Fig 2 D-optimal test design flowchart
本文选择了如表2所示的实验因素水平表,并结合上述公式进行优化设计分析.
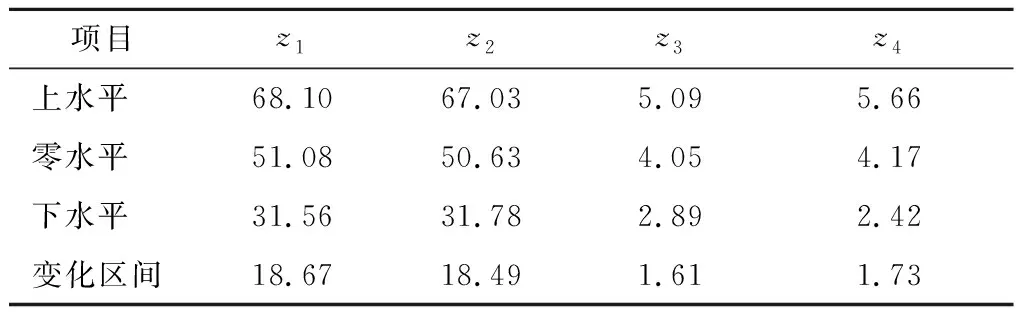
表2 实验因素水平表Tab.2 Level table test factors
最终得到4个实验因素16组不同的组合,将组合带入整车仿真模型中得到如表3所示,16组不同的悬架系数.

表3 仿真组合参数Tab.3 Combination simulation parameters
4 结果及分析
对麦弗逊式前悬架模型进行双轮平行跳动试验,结合表3进行D-最优试验优化,得出车轮外倾角、束角、轮速、滚动中心等参数,如图3~图9所示.

图3 侧倾转向角Fig.3 Roll steering angle

图4 侧倾外倾系数Fig.4 Roll camber coefficient
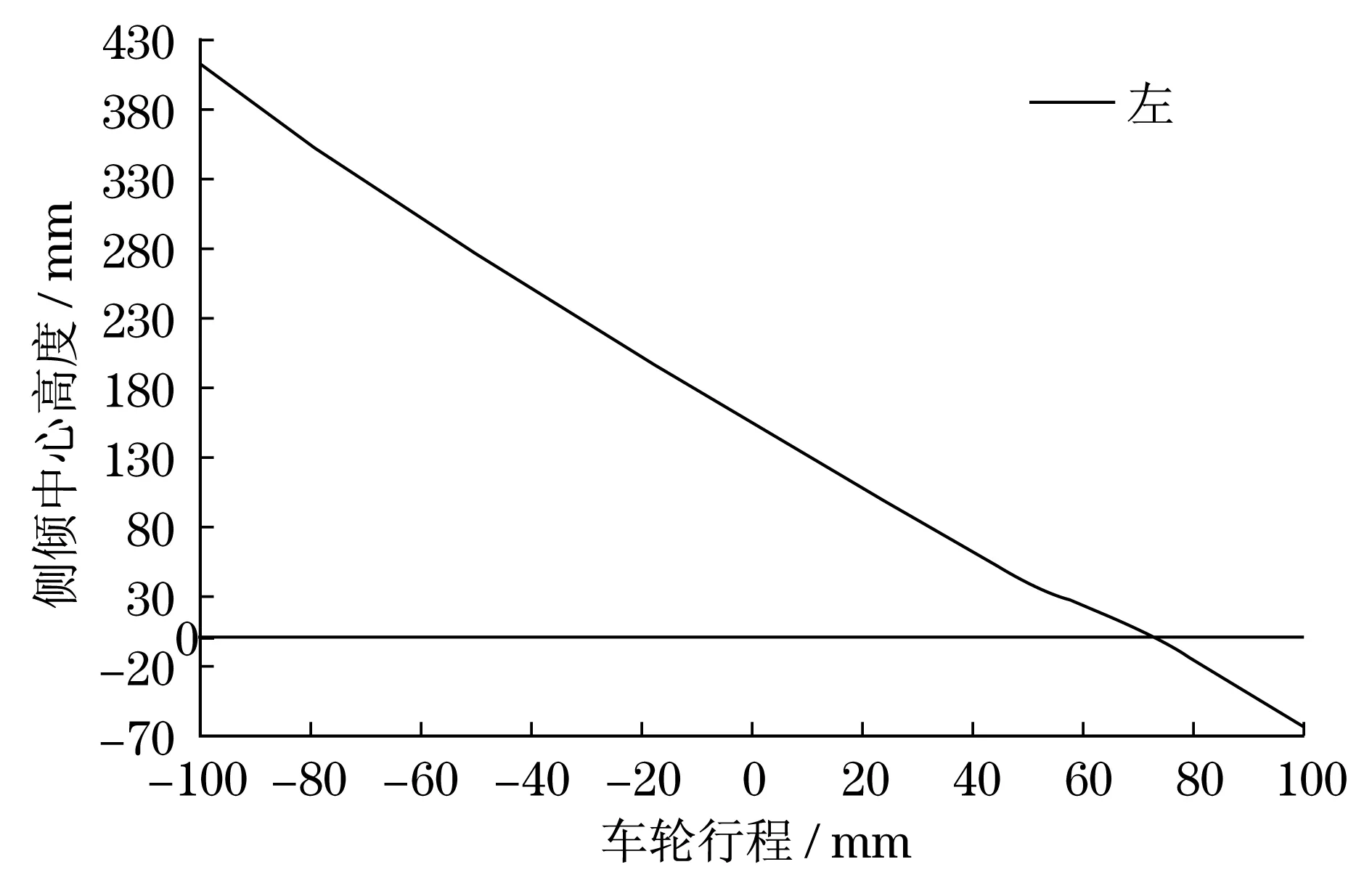
图5 侧倾中心高度Fig.5 Roll center height
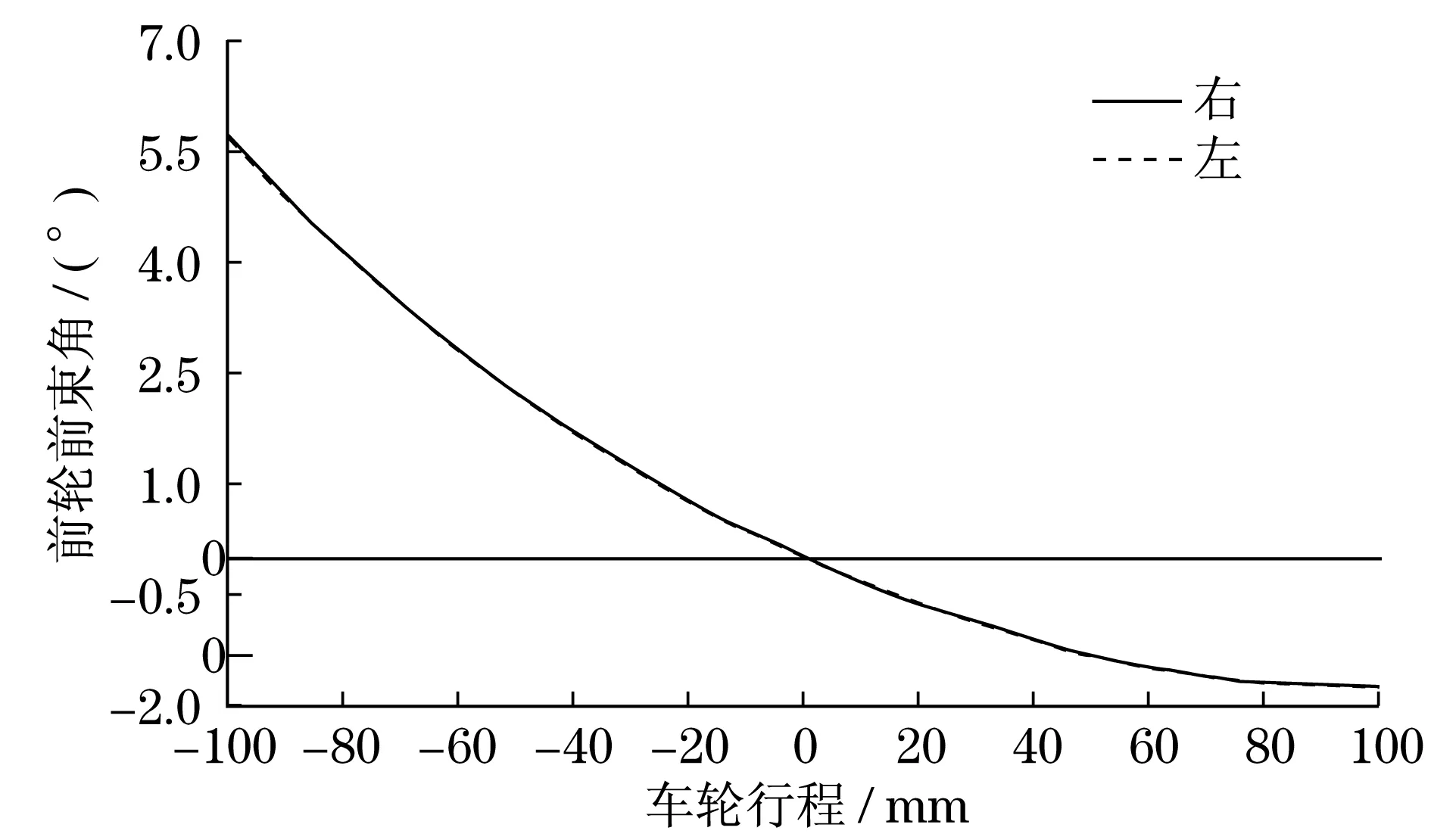
图6 前轮前束角Fig.6 Front toe angle

图7 前轮外倾角Fig.7 Front wheel camber

图8 悬架刚度Fig.8 Suspension stiffness

图9 主销纵倾移距Fig 9 Scrub Radius
从图3~图9可见:随着车轮跳动量的增加,侧倾转向角、侧倾外倾系数、侧倾中心高度、前轮前束角、前轮外倾角呈降低趋势,而悬架刚度和主销纵倾移距却是上升的趋势.当车轮跳动在80 mm左右时,悬架的刚度更强,此时的直观感受就是悬架过硬,舒适度不高.转向轮扭矩与转角关系如图10所示.由图10可知,由于悬架转向机构的特殊,前段转向角与车轮产生扭矩反应比较迟钝,中后段转向角与车轮的响应比较线性,更符合现代汽车的驾驶方式,避免直线行驶时方向盘的轻微波动带来的车辆方向偏动,提高了行驶安全性.

图10 转向轮扭矩与转角关系曲线Fig.10 Steering wheel torque and rotation curve
转向角与主销偏移距之间的关系如图11所示.从图11可知,随着转向角度增加,主销偏移距减小,且主销偏移距越小,在大幅度转弯时,车辆稳定性更高.优化后数据如表4所示.

图11 转向角与主销偏移距之间的关系Fig.11 Relationship between steering

5 结语
本文针对麦弗逊式悬架,利用D-最优试验设计进行了一系列优化.通过ADAMS/CAR模块建立了麦弗逊独立悬架的多体动力学模型,将麦弗逊悬架模型与随机路面模型相结合,并进行了D-最优试验法分析得到一系列优化后的悬架参数曲线.最终得出优化后的麦弗逊悬架在综合性能参数上都优于未优化之前,大大改善了汽车操纵稳定性和舒适性.
