采用Solidworks弧面分度凸轮建模新方法及静态分析

张文光,王大镇,应 帅,刘 辑,袁静云

(1.吉安职业技术学院 机械与电子工程学院,江西 吉安 343000; 2.集美大学 机械与能源工程学院,福建 厦门 361021; 3.吉安职业技术学院 公共基础课教学部,江西 吉安 343000)

弧面分度凸轮机构是一种间歇传动机构,其输入轴与输出轴处于垂直状态,与涡轮蜗杆传动比较相似[1].与连杆传动机构相比,弧面分度凸轮传动机构具有许多优点:① 构造简单,所占空间小;② 连接紧密,承载力大;③ 传动效率高,振动噪声较小.弧面分度凸轮机构应用较为广泛,主要应用于包装机械、飞机起落架、换刀机械手及精密机加工装备等许多领域.随着先进技术的发展,弧面分度凸轮机构更新速度也越来越快,对弧面分度凸轮承载能力也提出了更高要求.因此,研究弧面分度凸轮建模周期,延长其使用寿命具有重要的意义.

当前,研究人员采用不同方法对弧面分度凸轮建模进行深入研究.例如:文献[3]采用Imerageware和UG软件研究弧面分度凸轮三维建模和加工仿真,使用编程软件VC++对弧面分度凸轮进行参数化设计和计算,得出坐标点后导入到Imerageware中生成云图,通过UG软件生成弧面分度凸轮实体,并且对凸轮加工进行了仿真.文献[4]采用UG NX研究了弧面分度凸轮机构数字化三维模型,创建了滚子运动轨迹方程式,将方程式引入到UG NX软件中自动生成曲线,根据线、面、体方法生成三维模型,改变参数即可生成新的三维模型.文献[5]采用了Matlab和Solidworks软件研究了弧面分度凸轮三维建模和运动仿真,使用Matlab软件对弧面分度凸轮运动轨迹进行编程和计算,将计算数据插入到Solidworks软件中生成曲线,通过曲线生成曲面,曲面切割弧面分度凸轮毛坯,从而完成弧面分度凸轮的建模,并且对弧面分度凸轮进行了运动仿真.但是,以往研究的弧面分度凸轮建模周期长,所能承受的外界冲击力较小.对此,本文以弧面分度凸轮驱动12个滚珠运动为参照标准,建立其传动机构简图模型.选择改进正弦加速度运动规律曲线函数为滚珠运动轨迹,采用Matlab和Solidworks软件建立驱动滚珠运动的弧面分度凸轮实体模型.在Solidworks/Simulation环境中进行静力学分析,并与其他建模方法和静力学分析结果进行比较,为缩短弧面分度凸轮建模周期、延长使用寿命提供了参考价值.

1 弧面分度凸轮简图模型

按照弧面分度凸轮头数划分,可以将弧面分度凸轮分为单头、双头和多头[6].本文研究的是驱动12滚珠运动的单头弧面分度凸轮,其简图模型如图1所示.

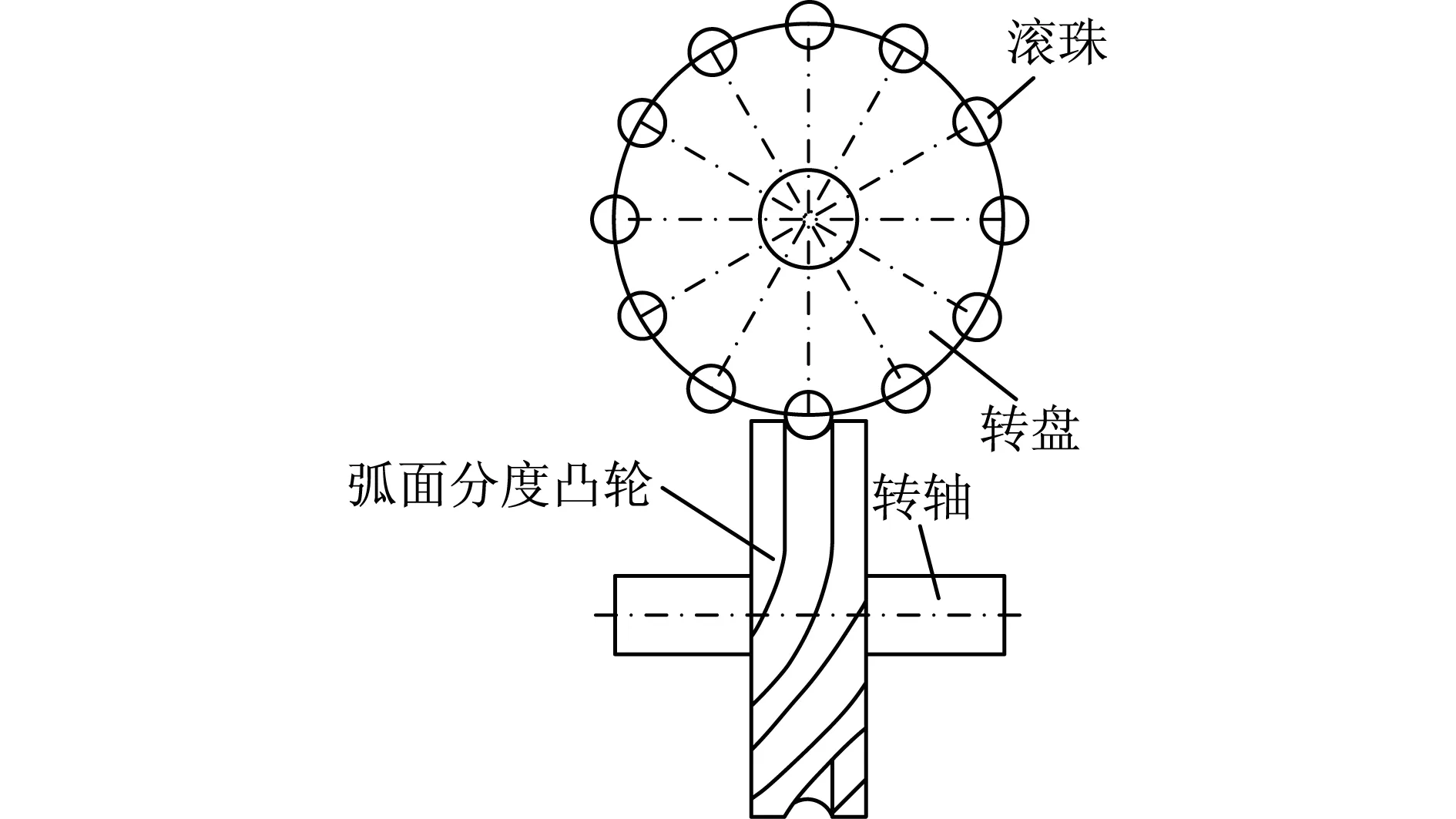
图1 弧面分度凸轮传动机构平面简图Fig.1 Plane diagram of globoidal indexing cam

其工作原理为:电动机输出轴与转轴接通后,通过转轴的键槽带动弧面分度凸轮旋转,弧面分度凸轮驱动滚珠绕着转盘中心进行旋转,滚珠带动转盘进行旋转.驱动转盘运动包括两个部分——停歇期和分度期.在停歇期内,可以加工转盘上产品;在分度期内,可以输送转盘上加工完成的产品.

2 滚珠运动规律设计

滚珠(凸轮从动件)运动的角位移设计特别重要,直接影响转盘的角速度、角加速度及角跃度的变化.转盘在运动过程中,要尽可能降低角速度、角加速度及角跃度的峰值.滚珠运动规律分为两个阶段——停歇期和分度期,停歇期运动相对简单,分度期运动较为复杂.当前滚珠运动规律[7-8]主要包括:① 正弦加速度运动规律;② 余弦加速度运动规律;③ 改进正弦加速度运动规律;④ 改进等速度运动规律;⑤ 改进梯形加速度运动规律;⑥ 3-4-5次多项式运动规律.通过Matlab软件分析和对比,采用改进正弦加速度运动规律作为滚珠分度期运动规律.分度期运动包括分度前期、分度中期和分度后期3个部分.

分度前期计算公式[9-10]为

(1)

分度中期计算公式[9-10]为

(2)

(1/8≤T≤7/8)

分度后期计算公式[9-10]为

(3)

(7/8≤T≤1)

式中:S为无量纲位移;V为无量纲速度;A为无量纲加速度;J为无量纲跃度;T为无量纲时间.

结合弧面分度凸轮运动过程,采用Matlab软件分析滚珠分度期运动规律计算公式,结果如图2所示.根据图2可知,滚珠带动转盘旋转过程中,并没有发生突变状况,满足设计要求.

3 弧面分度凸轮建模及静态分析

3.1 弧面分度凸轮实体建模

根据空间直角坐标系,可以推导出弧面分度凸轮驱动滚珠运动的分度曲面方程式[11-12]为

图2 滚珠分度期运动规律Fig.2 Motion law of ball grading

(4)

式中:r为滚珠到转盘中心距离;θ为凸轮角位移;φ为转盘角位移;p为弧面分度凸轮旋转方向,p=1为左旋,p=-1为右旋;C为转盘中心到弧面分度凸轮的中心距离;R为滚珠半径.

假设滚珠半径R=0,则式(4)变为

(5)

弧面分度凸轮实体建模的几何参数是设计者给定的,如表1所示.

根据表1几何参数,在Solidworks三维软件中创建驱动滚珠弧面分度凸轮毛坯实体,如图3所示.

根据式(1)～式(3)和式(5)、弧面分度几何参数,在Matlab软件中编写弧面分度凸轮驱动滚珠运动轨迹程序,计算和输出运动轨迹三维坐标点数据,将此数据保存在文本文档中.在Solidworks三维软件中打开弧面分度凸轮毛坯实体,插入滚珠运动轨迹三维坐标点拟合曲线后,如图4所示,而文献[5]插入滚子运动轨迹三维坐标点拟合曲线后,如图5所示.

在图4曲线垂直方向上创建一个圆形,直径为20 mm,通过扫描切除弧面分度凸轮毛坯,如图6所示.在图5中,两条曲线拟合成一个曲面,设置曲面对称偏置距离为20 mm,通过曲面偏置切除弧面分度凸轮毛坯,如图7所示.

表1 弧面分度凸轮几何参数值Tab.1 The geometric parameter value of the

图3 弧面分度凸轮毛坯Fig.3 Globoidal indexing cam blank

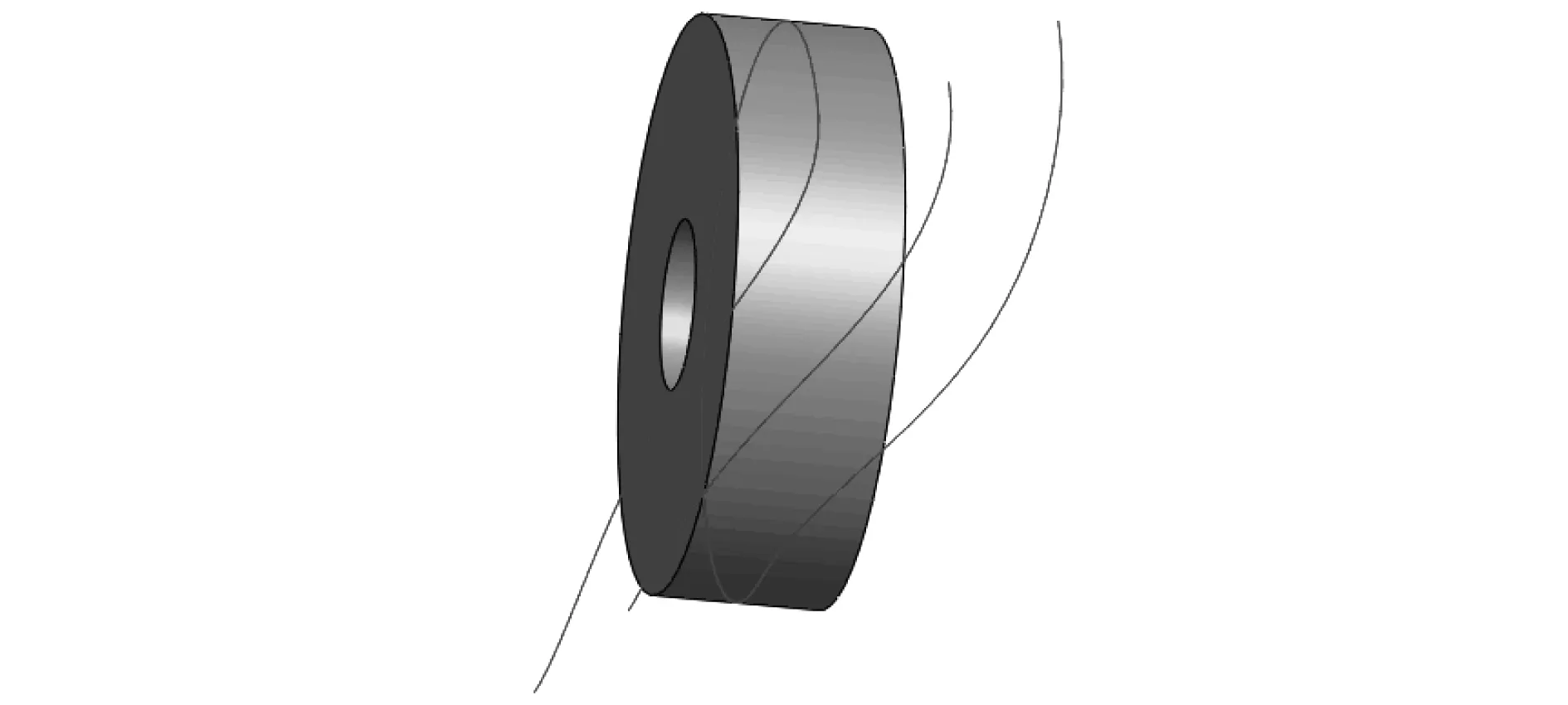
图4 滚珠拟合曲线Fig.4 Ball fitting curve

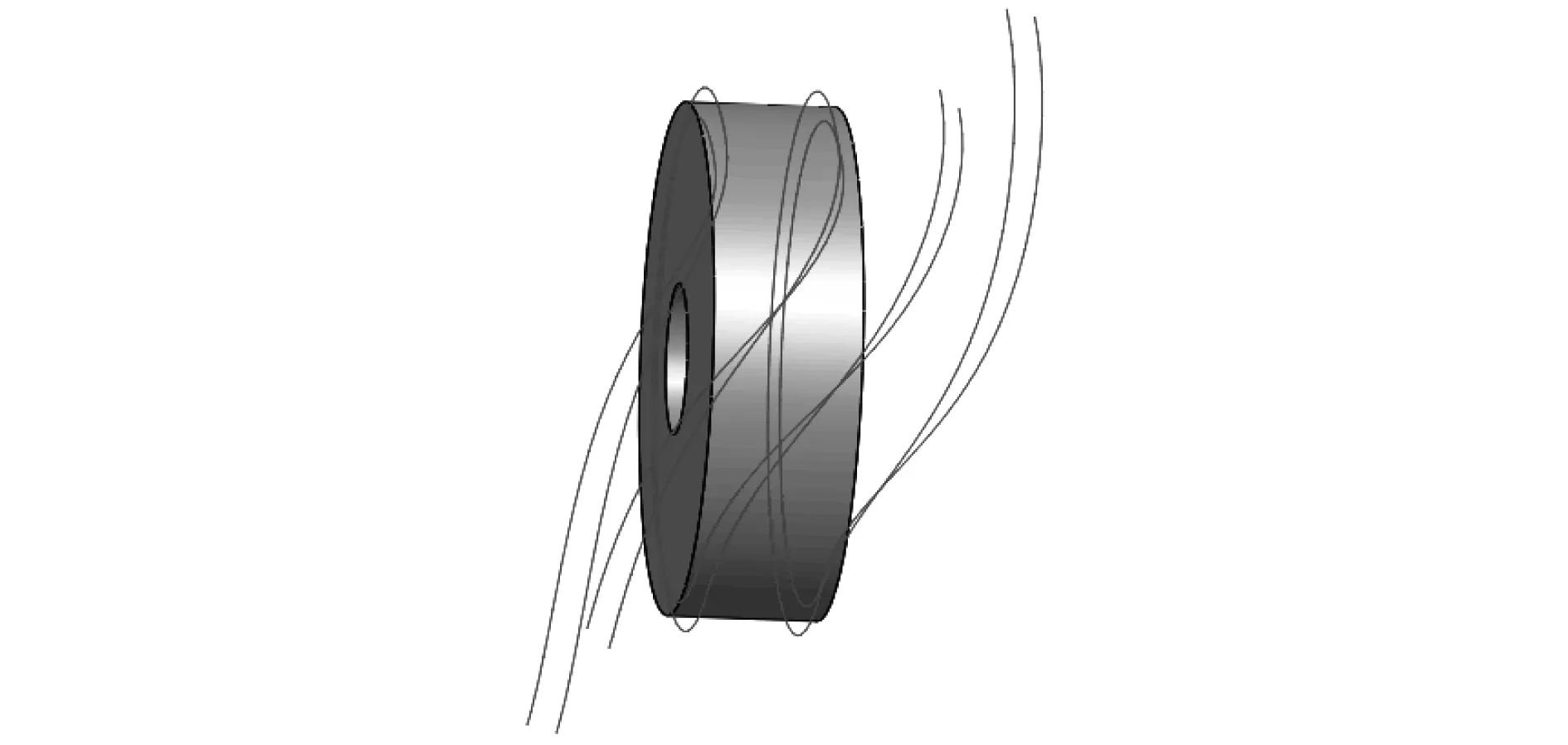
图5 滚子拟合曲线[5]Fig.5 Roller fitting curve[5]

图6 驱动滚珠分度凸轮Fig.6 Drive ball indexing cam

图7 驱动滚子分度凸轮[5]Fig.7 Drive roller indexing cam

对比图4和图5可知,驱动滚珠分度凸轮运动轨迹所需2条运动轨迹曲线,而文献[5]驱动滚子分度凸轮运动轨迹所需4条运动轨迹曲线.因此,驱动滚珠弧面分度凸轮建模速度快,缩短了弧面分度凸轮开发周期.

3.2 静态分析

Solidworks三维软件功能比较强大,可以对三维实体模型进行静态分析.当前静态分析软件大多采用ANSYS,但是必须要将三维实体模型转换为IGES格式,导入到ANSYS过程中,也容易造成数据的丢失.因此,采用Solidworks中静态分析模块,可以避免软件之间的数据交换,提高了三维实体模型静态分析的准确性.采用Solidworks软件的有限元模块Solidworks/Simulation对弧面分度凸轮进行静态分析,凸轮材料参数如表2所示,分度曲面冲击力F=105N,驱动滚珠弧面分度凸轮应力、位移图解如图8和图9所示,而文献[5]创建的驱动滚子弧面分度凸轮应力、位移图解如图10和图11所示.

表2 弧面分度凸轮合金钢材料Tab.2 Globoidal indexing cam alloy steel material

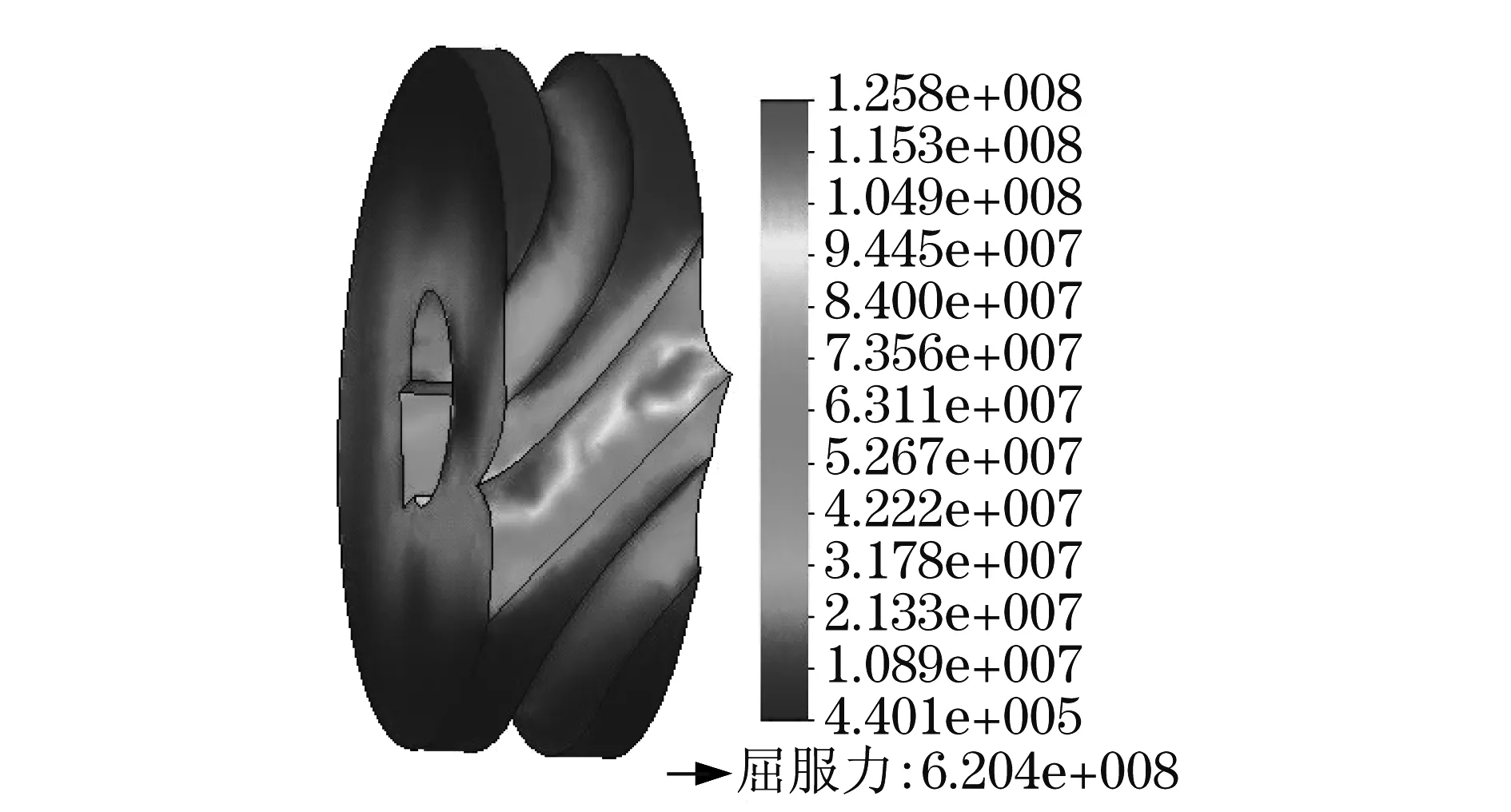
图8 驱动滚珠凸轮应力图解Fig.8 Stress diagram of driving ball cam

图9 驱动滚珠凸轮位移图解Fig.9 Displacement diagram of driving ball cam

图10 驱动滚子凸轮应力图解[5]Fig.10 Stress diagram of driving roller cam[5]

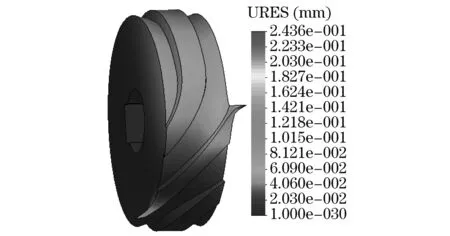
图11 驱动滚子凸轮位移图解[5]Fig.11 Displacement diagram of driving roller cam[5]

根据图8～图11可以得到静态分析数据如表3所示.

表3 弧面分度凸轮静态分析参数Tab.3 Static analysis parameters of globoidal

根据表3可知:驱动滚珠弧面分度凸轮在冲击力F=105N的作用下,产生最大应力值为1.258×108N/m2,小于屈服强度值,不会发生断裂现象;而驱动滚子弧面分度凸轮在冲击力F=105N的作用下,产生最大应力值为1.419×109N/m2,大于屈服强度值,凸轮会发生断裂现象.另外,驱动滚珠弧面分度凸轮产生的最大位移值小于驱动滚子凸轮,驱动滚子弧面分度凸轮在冲击力作用下,变形较为严重.因此,驱动滚珠弧面分度凸轮,能够承载更大的冲击力,使用寿命更长,效果更好.

4 结语

针对弧面分度凸轮建模问题,采用了改进正弦加速度运动规律作为滚珠运动轨迹,并且对弧面分度凸轮实体进行静态分析,主要结论如下:

(1) 弧面分度凸轮采用改进正弦加速度运动规律驱动滚珠运动,没有发生突变现象,满足设计要求;

(2) 与驱动滚子运动的弧面分度凸轮相比,驱动滚珠运动的弧面分度凸轮实体模型,建模速度快,缩短了弧面分度凸轮的研发周期;

(3) 弧面分度凸轮工作曲面在受到连续冲击力的作用下,与驱动滚子运动的弧面分度凸轮相比,驱动滚珠运动的弧面分度凸轮实体模型承载力更大,使用寿命较长.