超宽凸缘首次拉深模型
2018-10-30王跃静
王跃静
(上海交通大学 机械与动力工程学院)
0 引言
随着汽车技术的迅速发展,电子控制单元被广泛的应用于汽车总成模块。 在汽车许多电子控制单元上都需要罩盖(ECU cover)。 通常罩盖是钣金拉深而成的。有一些助力转向中电子控制单元的罩盖是形状特别复杂的拉深件。参见图1。
这个零件的难点有两个地方第一各个部位的圆角相对产品的拉深高度比较小;第二底部的圆筒拉深的可行性。第二个问题是本文讨论的主要问题。在没有法兰或者是窄法兰甚至是宽法兰的情况下,本产品拉深可行性没有任何问题,按照冲压手册介绍的拉深方法是可以完成的。但是本产品展开以后法兰实在太大见图2,以至于不能在相关的参考书找到行之有效的方法来制定拉深工艺。
决定拉深工艺是否可行通常有几个重要因素:几何形状,拉深间隙,合模高度,模具表面摩擦力和材料的选择。最后四个因素可以在Dynaform中自由的设置,但是几何形状变化万千。圆筒件拉深初始时凸模底部首先接触材料然后带动材料逐渐进入凹模,拉深初始凸模圆角最下部位的直径大大小于凹模圆角最上部的直径[1]。 它们之间的间隙使得材料在拉深开始时都是以圆台或者类似圆锥的形式进入凹模的, 随着拉深的高度的增加,圆台或者类圆锥的斜度逐渐从水平方向变化到靠近竖直方向。 拉深的不同阶段的不同形状都可以用来作为超宽凸缘的初次拉深。

图1 罩盖产品图Fig.1 Cover product

图2 圆筒法兰图Fig.2 Cylinder flange
1 超宽凸缘拉深
根据冲压手册中定义出无凸缘,窄凸缘,宽凸缘[2]。窄凸缘的凸缘直径和拉深直径比值在1.1~1.4之间;窄凸缘的凸缘直径和拉深直径比值大于1.4。由于冲压手册中给出的拉深系数和拉深高度的经验值都是在凸缘直径和拉深直径比值小于等于3.0条件下的。将凸缘直径和拉深直径比值大于3.0的拉深件定义为超宽凸缘拉深件。
2 母线形状
研究的圆筒拉深是旋转体,可以通过研究母线来简化过程。根据实际生产中的经验和拉深过程中的产品形状,总结了以下比较适合拉深的六种旋转体形状作为研究的对象。见图3。

第一母线

第二母线

第三母线

第四母线

第五母线

第六母线
图3 六种母线图
Fig.3 Six kinds of busbars
根据冲压手册上讲述的拉深凹凸模圆角的关系[2]:凸模圆角是凹模圆角的0.6~1.0倍。为了尽可能使在首次拉深底部圆角面积大,变薄均匀,所以选取最大系数1.0得到了凹凸模圆角大小相同;规定了每个模型凹模圆角r和最大外径D取相同的值;要研究模型的优劣就要在拉深量基本相同的基础上做研究,这样根据拉深面积相等可以计算出R或者h。
3 模型的建立


表1 不同r,D时h,R的取值Table 1 The values of H and R at different R0 and D levels
当毛坯直径取值200 mm和拉深筒径为60 mm,材料厚度取值0.5 mm时可以计算出凸缘直径,求得以上18中模型比值在3.10~3.29之间,全部大于超宽凸缘最小值3.0,属于超宽凸缘。
表1中列出了画出母线所需要的全部参数值,在AutoCAD中按照参数值作出这18个试验模型的母线及中心线。导入UG,做出凹凸模和压料板,最后作出毛坯板料面并且按照实际的模具动作状态的初始位置放置。冲压方向是Z轴的负方向。
4 Dynaform设置
选取DC05为拉深材料,使用预置的材料性能参数。选用Shell单元,五个积分点,毛坯最大网格尺寸为5,壳单元;模具的网格最大尺寸为10,最小为0.2,弦高误差为0.05,角度为8,间隙公差为0.8[3];摩擦系数设定为0.05;闭合和拉深速度设定为1000 m/s,压料力经过计算设定为2000 N;间隙设定为1.1T+0.02材料下公差(1.1倍的材料厚度+预计的材料下公差)。
5 模拟结果
第一种圆角接半球母线,从图4可以清楚看出此种母线旋转体在拉深过程中最先接触材料的顶部变薄率最大,如果除去材料各向异性的影响,材料变薄率从顶部向下逐渐减小。在整个拉深过程中对于整个产品的受到的拉力是持续的变大。由于越靠近顶部半径越小,受到拉力越大,所以变薄率越大。第二种圆角接直壁母线,从图5可以清楚看出此种母线旋转体在拉深过程中最先接触材料的顶部是平面,所以底部受力均匀。在实际经验中开裂风险主要集中在底部圆角和直壁结合部,特别是当凸缘以及凸缘相接的上部圆角的材料厚度增加使得材料难以顺利流入凹模,拉力会增大很多使得在底部圆角和直壁结合部受到更大拉力,这个拉力的大小决定材料是否破裂。第三种圆角接拔模角度母线,图6所示母线的拉深状态与第二种母线很接近,通过数值模拟最大变薄率明显大于第2种母线。 通常拔模角度设置为3度。

图4 第一母线数值模拟图Fig.4 The first bus numerical simulation value

图5 第二母线数值模拟图Fig.5 The second bus numerical simulation value

图6 第三母线数值模拟图Fig.6 The third bus numerical simulation value
第四种圆角接圆角母线,图7所示圆角接圆角的母线实际上是第二种母线拉深过程中的一个时刻的形状。第五种圆角接斜角母线,图8所示母线实际上是第二或者三种母线拉深过程中的一个时刻的形状。在这里斜角设置为30度,如果太大的话整体材料流入量太小,会导致顶部太尖,应力集中。如果太小,比较接近直壁,没有研究价值。第六种圆角接圆弧母线,图9所示圆角接圆弧母线同样也是圆角接半圆母线拉深过程中的一个时刻的形状。

图7 第四母线数值模拟图Fig.7 The fourth bus numerical simulation value
当拉深量是一致时,在这里材料变薄量是判断模型优劣的标准。由于前三种拉深量是一致,后三种拉深量一致,可以分两组比较。为了方便研究我们选取凸凹模圆角相同,筒径和高度不同。根据表1做出18种母线模型来做试验模拟。实验结果见表2:
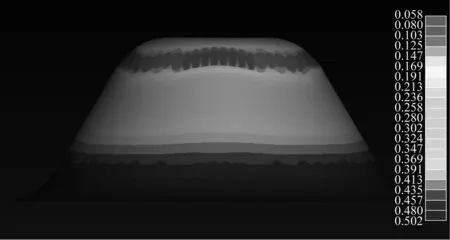
图8 第五母线数值模拟图Fig.8 The fifth bus numerical simulation value

图9 第六母线数值模拟图Fig.9 The sixth busbar numerical simulation value

表2 拉深后材料厚度极值Table 2 The extreme value of material thickness after drawing
表2是上述的18种母线旋转体数值模拟的厚度变化数据,在材料变厚方面数值很小可以忽略这个因素,主要看材料变薄量。可以做出比较图10和图11。

图10 第一二三母线数值模拟材料厚度
Fig.10 The first、 second、 and third busbar numerical simulation material thickness

图11 第四五六母线数值模拟材料厚度
Fig.11 The fourth, fifth, and sixth busbar numerical simulation material thickness
如图10所示,在第一组的三种母线三种圆角的实验中没有明显数据显示哪种母线旋转体厚度变化优于其它。很明显第一组实验的拉深量太大,导致材料破裂太多,但是足以说明不适合超宽凸缘的首次拉深。在图11第二组实验中可以明显看出是第四种类型的母线模型材料变薄量小于其它,是最佳选择。通过18次实验的数据可以得出第四种母线的旋转体模型最适合超宽凸缘的首次拉深。
5 总结
定义了凸缘直径和拉深直径比值大于3.0的是超宽凸缘拉深。在第一组实验中,材料变薄率非常大,开裂风险非常大,所以第一组三种母线模型不适合超宽凸缘首次拉深。在第二组实验中,第四种母线模型三种不同大小圆角的数值模拟结果全部都是材料变薄量最小的。通过对大小不同圆角的母线旋转体模型共18种,模拟验证找到了最适合第一步超宽凸缘拉深的模型是圆角和圆角相接的母线旋转而成的第四种模型。在罩盖的实际生产中应用,提高了产品质量,降低了后续拉深的难度。
