一类基于相关性准则的广义加权组合评价模型

储 震，杨桂元

（1.安徽财经大学 数量经济研究所，安徽 蚌埠 233030；2.同济大学 经济与管理学院，上海 201800）

0 引言

在对某种经济问题进行单项评价时，人们往往只能得到比较片面的结果。为了规避由此带来的评价偏差，有效地整合各种评价方法的信息，学术界提出了“组合评价”的思想[1-3]。目前国内外学者关于组合评价的理论研究主要集中在评价权重的组合和评价结果的组合这两个方面。关于评价权重的组合，汪泽焱[4]和陈伟[5]等基于加以区别的主客观权重向量集进行了最优化权重组合；林元庆[6]基于不加以区别的主客观权重向量集进行了最优化权重组合。关于评价结果的组合，郭显光[3]等基于评价序值向量集进行了最优化组合赋权；郭亚军[7]和陈国宏[8]基于评价数值向量集进行了最优化组合赋权。通过对比发现，李珠瑞等[9]认为运用评价值进行组合能最大限度地集结原始信息而最小化偏差，从而使组合评价值更接近真实值。随之组合评价理论的不断丰富和发展，近些年，李珠瑞[9]和彭张林[10]等也相继提出了基于离差最大化、评价结论的二次组合的新方法。

通过梳理相关文献可以发现，面对评价问题“真实值”的不可观测性，优化组合理论似乎出现了某种“失灵”现象；与此同时，多数研究还只是处在初步尝试阶段，部分研究成果的科学性与合理性还有待理论检验。鉴于此，本文遵循“少数服从多数”和“整体贴近度最大化”等思想构建了一类基于相关性准则的广义加权组合评价方法，在给出了优性组合评价以及冗余度等概念的基础上对其有效性进行了理论推导，最后结合实例计算更进一步进行了佐证。

1 基于相关性准则的广义加权组合评价模型的概念

设有n个评价单元，分别采用m种评价方法对其进行评价，构成数据阵{xij}n×m，其中 xij是第i个评价单元运用第 j种评价方法所得到的评价值。为了更充分地整合各评价方法所包含的评价信息，依据组合理论，可以得出以下相关基本概念[11-13]。

定义1：若组合评价模型采用如下的非线性加权平均形式：

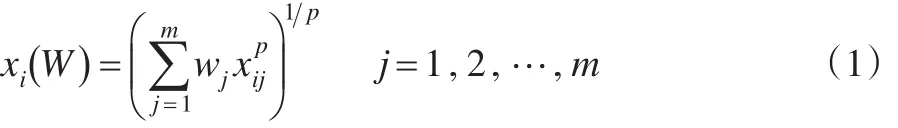
则称该组合评价方法为广义加权算术平均组合方法，其中，xi为各评价单元的组合评价值，wj表示第 j种单项评价方法在组合评价方法中的权系数，

定义2：称ρj为组合评价值序列与第 j种单项评价值序列的相关系数，ρkj为第k种单项评价值序列与第 j种单项评价值序列的相关系数（0≤ρ≤1）。

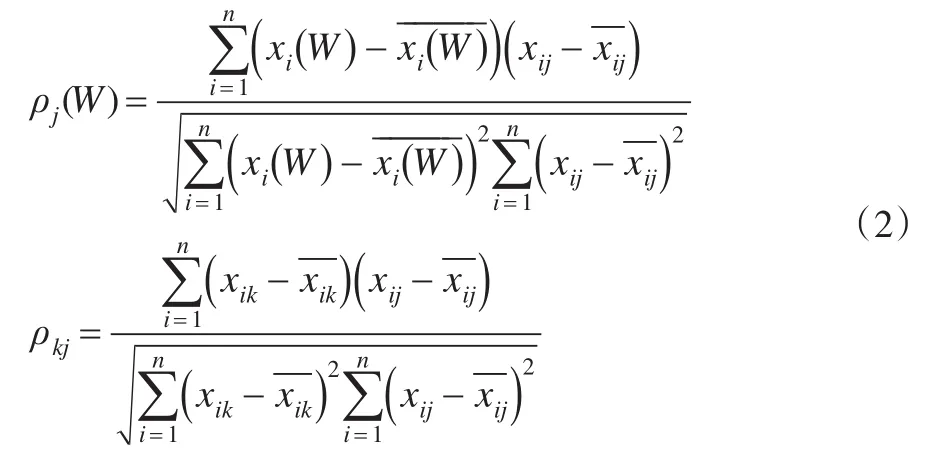
不难看出，组合评价方法的相关系数是关于各单项评价方法的权重向量W的一个函数，故可记为R(W)。为有效提高组合评价结果与各单项评价结果吻合度，即使得各评价单元能够被更客观地评价，根据相关系数的性质，我们希望组合评价值与各单项评价值向量之间的相关系数之和R(W)愈大愈好，为此本文建立如下基于相关系数的组合评价模型：

定义3：称ηj为组合评价值序列与第 j种单项评价值序列的向量夹角余弦，ηkj为第k种单项评价值序列与第j种单项评价值序列的向量夹角余弦（0≤η≤1）。

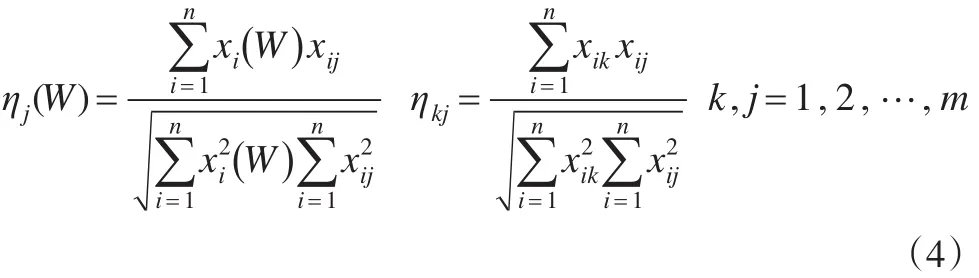
不难看出，组合评价方法的向量夹角余弦是关于各单项评价方法的权重向量W的一个函数，故可记为S(W)。为有效提高组合评价结果与各单项评价结果吻合度，即使得各评价单元能够被更客观地评价，根据向量夹角余弦的性质，组合评价值向量与各单项评价值向量之间的向量夹角余弦之和S(W )愈大愈好，为此，本文建立如下基于向量夹角余弦的组合评价模型：

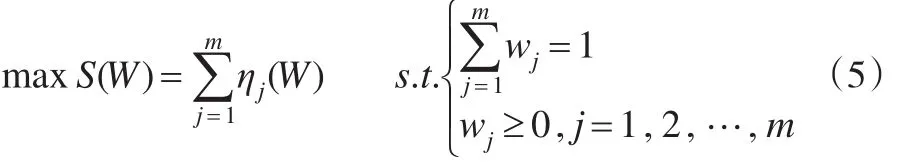
定义4：称γj为组合评价值序列与第 j种单项评价值序列的灰关联度，γkj为第k种单项评价值序列与第 j种单项评价值序列的灰关联度（0≤γ≤1）。

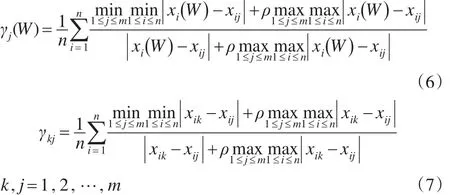
不难看出，组合评价方法的灰关联度是关于各单项评价方法的权重向量W的一个函数，故可记为Q(W)。为有效提高组合评价结果与各单项评价结果吻合度，即使得各评价单元能够被更客观地评价，根据灰关联度的性质，我们希望组合评价值与各单项评价值向量之间的灰关联度之和Q(W)愈大愈好，为此本文建立如下基于灰关联度的组合评价模型：

定义 5：若满足 Rmin≤R(W*)≤Rmax(Smin≤S(W*)≤Smax、Qmin≤Q(W*)≤Qmax)，则分别称基于相关系数（向量夹角余弦、灰关联度）准则下的组合评价模型为非劣性组合评价；若R*＞Rmax(S*＞Smax、Q*＞Qmax)，则称之为优性组合评价；若 R*＜Rmin(S*＜Smin、Q*＜Qmin)，则称之为劣性组合评价。其中W*为组合评价模型的最优权重向量。

定义6：在一个组合评价模型中，设共有m种单项评价方法参与组合评价。若某种单项评价方法在组合评价模型最优权系数中为零，则称该单项评价方法为冗余评价方法。即该种单项评价方法增加到组合评价模型中不能增加组合评价的相关系数（向量夹角余弦、灰关联度），表明该种单项评价方法只提供冗余信息。若最优解中出现冗余评价方法的个数为m′，则称比例r=m′m为组合评价模型的冗余度。

2 基于相关性准则的广义加权组合评价模型的性质定理

定理1：基于相关系数（向量夹角余弦、灰关联度）准则下的组合评价模型的最优目标函数值均是参与组合评价的各单项评价方法总个数m的单调不减函数，即：

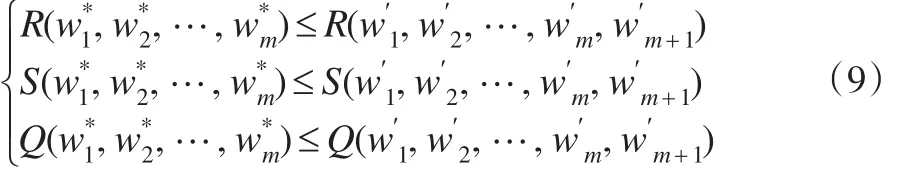
设表示m+1个单项评价方法参与的基于相关系数准则下的组合评价模型的最优解。则：

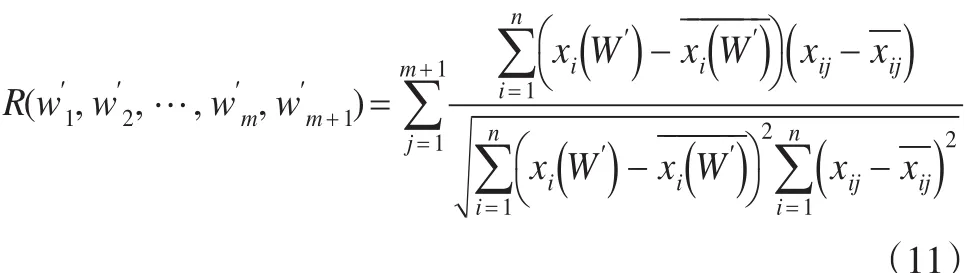
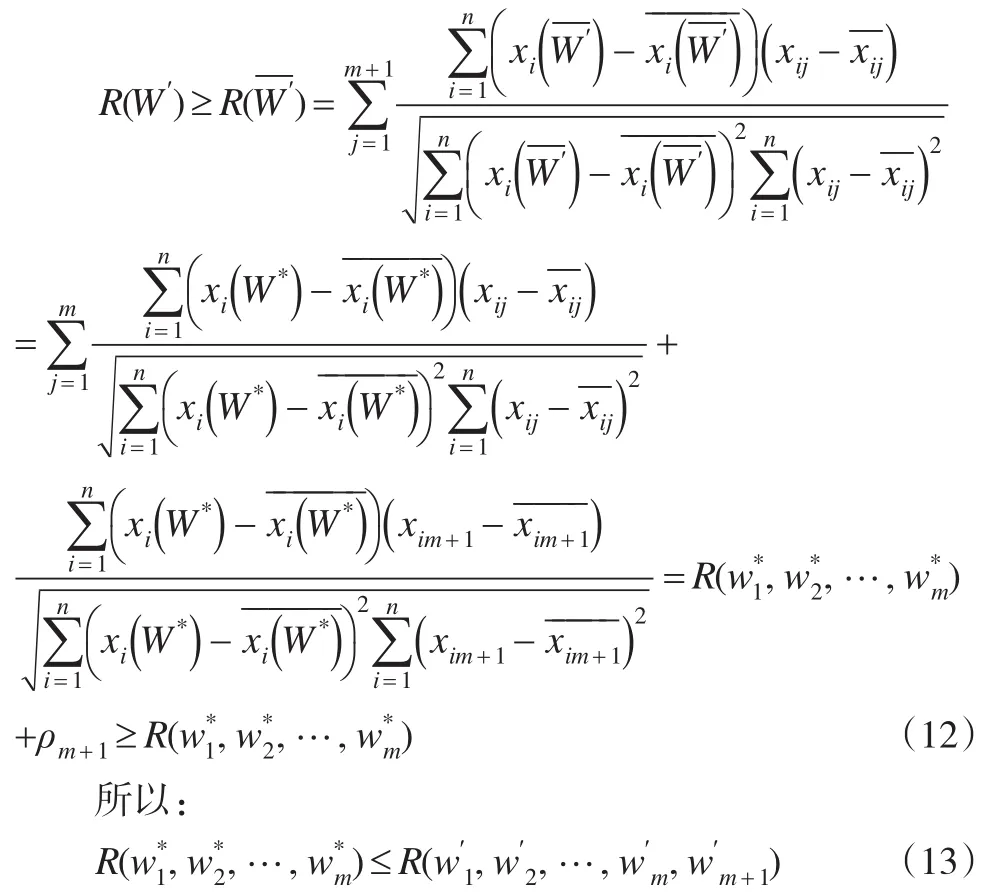
即证基于相关系数准则下的组合评价模型的最优目标函数值是参与组合评价的各单项评价方法总个数m的单调不减函数。

同理可证：

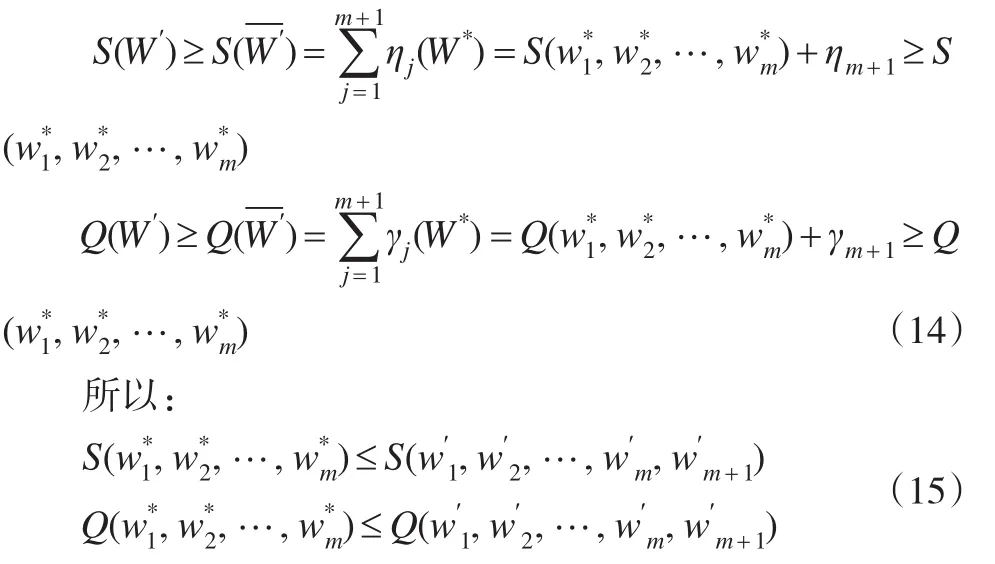
即证基于向量夹角余弦、灰关联度准则下的组合评价模型的最优目标函数值均是参与组合评价的各单项评价方法总个数m的单调不减函数。

由定理1可知，再增加一个单项评价方法的组合评价模型对应的最大的相关系数（向量夹角余弦、灰关联度）可能不变，这表明组合评价模型可能存在冗余评价方法。

定理2：基于相关系数（向量夹角余弦、灰关联度）准则下的组合评价模型的冗余度r＜(m -1)m,则最优解对应的组合评价一定是优性组合评价。

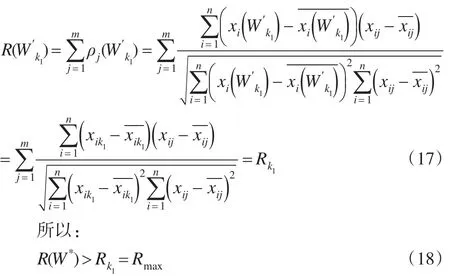
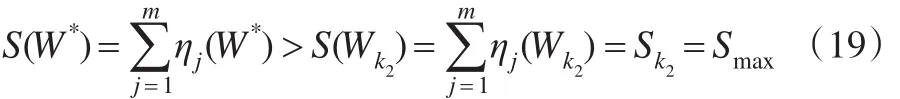
3 算例

3.1 计算步骤

基于相关性准则的广义加权组合评价可分为以下几个主要步骤来实施：

步骤2：计算归一化评价矩阵{xij}n×m，其中 xij表示评价单元i所对应的第 j种单一评价值。从各类综合评价方法中选取几种具有代表性的单一评价方法，分别对所提出的问题进行综合评价，并对评价矩阵按单一评价方法进行归一化处理，从而有效减少了因各方法结果之间差距太大所引起的对组合效果的影响。

步骤3：依据定义2至定义4计算基于相关性准则的广义加权组合评价xi(W )。首先运用Kendall一致性系数检验这几种单一综合评价方法的相容性；然后基于相关性准则的广义加权组合评价模型对上述几种相容评价方法的评价结果进行组合，得出组合评价值并进行排序。最后运用Kendall一致性系数检验组合评价方法与各种单一相容评价方法的密切程度。

3.2 算例分析

为了反映本文提出的基于相关性准则的广义加权组合评价的有效性，不失一般性，这里仅选取基于向量夹角余弦的算术平均组合评价方法加以探讨即可。围绕供给面风险、需求面风险以及金融面风险三个维度筛选出的能够有效测度我国房地产泡沫的六个指标，并应用来自中国统计年鉴与中国房地产统计年鉴的我国1998—2015年原始数据矩阵=()18×6进行实例分析。

按照步骤1及步骤2可计算出由熵值法、因子分析法和层次分析法3种不同的单项评价法分别来确定的综合评价值，进而得到归一化评价矩阵{xij}18×3，结果如表1所示。在此基础上，按照步骤3，利用LINGO软件对基于向量夹角余弦的算术平均组合评价模型计算出最优权系数分别表示为：w1=0.318，w2=0.287，w3=0.395。并由此得到组合评价值，结果如表1所示。

表1 我国楼市泡沫的各项评价结果

在评价基于向量夹角余弦的组合评价模型的有效性时，可通过构建如下误差评价指标体系予以论证：

与预测问题相比较，评价问题的真实值比较难确定。根据中心极限定律，在没有其他更好的替代方案情况下，取相容方法集中多方法的平均值序列{x ˉi，i=1，2，…，n}作为第i个评价单元的基准评价值。

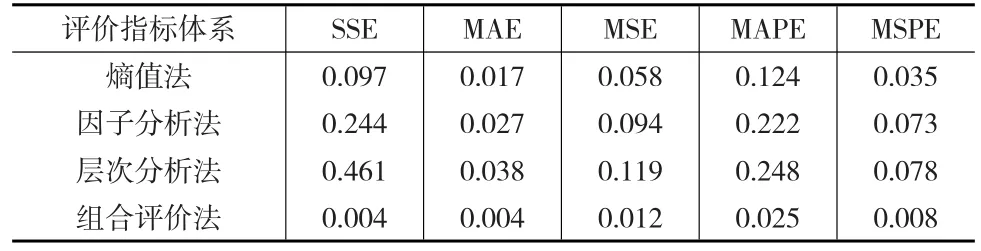
表2 效度评价指标体系

由表2可知，相较于各单项评价方法，基于向量夹角余弦的组合评价模型的各种误差指标值要小得多。这在一定程度上佐证了一类基于相关性准则的广义加权组合评价方法要优于其他单项评价方法，能够很好地提高评价效度。

4 结束语

本文在现有文献的基础上，选用对多个单一评价方法的评价值进行组合的思路。首先，把“少数服从多数”和“整体贴近度最大化”等思想引入组合评价中，构建了一类基于相关性准则的广义加权组合评价模型。然后，对其相关性质作了研究，提出了优性组合评价、冗余度等概念，探讨了冗余评价以及优性组合评价方法的存在性的判定，得出一些有价值的结论，从理论上论证了这类最优组合评价方法确实能综合各种单项评价方法的信息。最后，结合我国房地产泡沫测度实例，进一步肯定了其在各评价领域中值得普遍应用和推广的价值。