灰色预测模型背景值构造的新方法
2018-10-30杨孝良
杨孝良,周 猛,曾 波
(重庆工商大学a.长江上游经济研究中心;b.国家智能制造服务国际科技合作基地,重庆 400067)
0 引言
灰色理论[1]是研究和解决现实世界不确定性问题的主要方法之一,以GM(1,1)模型为基础的灰色预测模型是灰色理论的重要组成部分,而背景值[2]则是影响灰色预测模型性能的重要参数之一。为了改善灰色预测模型性能,研究人员从不同角度对灰色预测模型背景值的构造方式与优化方法进行了深入研究,并取得了较为丰硕的研究成果。
灰色预测模型背景值构造方式的优化。灰色预测模型背景值z(1)(k)是一个平滑公式,当建模数据变化平缓时,通过紧邻均值来计算灰色预测模型背景值是合理的;反之,当建模数据具有一定的波动性或振荡特征时,假如同样使用z(1)(k)作为灰色预测模型背景值,往往导致灰色预测模型误差偏大。为了解决该问题,谭冠军[3]、刘乐[4]、蒋诗泉[5]等对灰色预测模型背景值的构造方法进行研究。如蒋诗泉[5]基于积分几何意义的视角,利用函数逼近的思想并结合复化梯形公式,提出了一种新的GM(1,1)模型背景值优化方法,所建立的GM(1,1)模型在预测精度上有显著的提高。
灰色预测模型背景值计算方式的优化。灰色预测模型背景值z(1)(k)=0.5x(1)(k -1)+0.5x(1)(k),换言之,建模时通过x(1)(k -1)与x(1)(k)的均值来作为灰色预测模型的背景值。实际上这是一种简化处理,为此,肖新平[6]、谢开贵[7]等将z(1)(k)推广为z(1)(k)=αx(1)(k -1)+(1-α)x(1)(k ),其中α∈(0,1)为待定参数,通常利用遗传算法等智能寻优算法来确定α的相对最优值,并称该模型为GM(1,1,α)模型。另外,李俊峰[8]、童明余[9]、刘震[10]等提出用插值和数值积分中的Newton-Cores公式、数值积分中的Gauss公式等来优化和改善灰色预测模型背景值,并将其应用于我国城市内分泌、营养和代谢疾病及免疫病致死人数占死亡总人数的百分比预测,取得了较好的效果。
灰色预测模型背景值构造的非等间距拓展。现有灰色预测模型主要研究和讨论等时距情况下的系统预测问题,实际上等时距只是一种理想情况,现实生活中大量实际应用是非等时距的。因此,如何在非等时距情况下实现灰色预测背景值的合理构造,是构建非等时距灰色预测模型的重要内容[11,12]。为此,李翠凤等[13]提出用 x(1)(t)在区间[ki, ki+1]中点的实际值来构造非等时距灰色预测模型的背景值;王叶梅等[14]根据灰色模型的指数特性和积分特点,利用非齐次指数函数来拟合一次累加生成序列,提出了一种重构非等间距灰色模型背景值的方法。
灰色预测模型背景值构造方式与计算方法的优化,对提高灰色预测模型模拟及预测性能,拓展灰色预测模型应用范围,丰富和完善灰色预测模型理论体系,具有重要的理论意义和应用价值。然而,现有灰色预测模型的构造或优化都是建立在x(1)(k -1)与x(1)(k)的基础之上,这导致灰色预测模型背景值容易受到建模序列中极端数据的影响,从而影响灰色预测模型性能。为此,本文提出一种灰色预测模型背景值构造的新方法。
1 NGM3(1,1)模型
定 义1:设 非 负 原 始 序 列Y(0)=(y(0)(1),y(0)(2),…,y(0)(m )) ,其中 y(0)(k )≥0,k=1,2,…m ,序列 Y(1)是序列Y(0)的1-AGO生成序列,即:
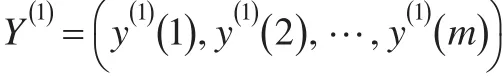
其中:
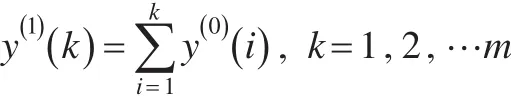
则,当k=3,4,…,m,

称公式(1)为背景值含三参数的新型灰色预测模型,简称NGM3(1,1)模型。
定理1:序列Y(0)及Y(1)如定义1所述,p^=(a ,b,c)T为NGM3(1,1)模型的参数列,且:
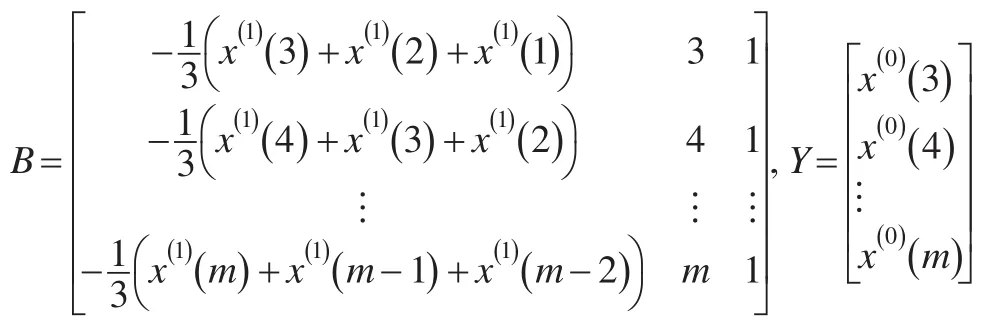
则称NGM3(1,1)模型的最小二乘估计参数列满足:
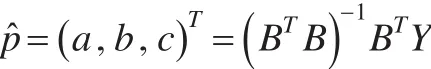
证明:将数据代入NGM3(1,1)模型,即公式(1),得:
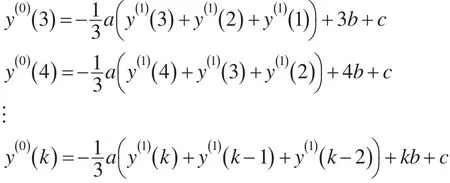
上述方程组的矩阵形式为:

对参数a,b及c的一堆估计值,以-a(y(1)(k)+y(1)(k -1)+y(1)(k -2))/3+kb+c来代替 y(0)(k ),k=3,4,…,m ,可得误差序列:

设:
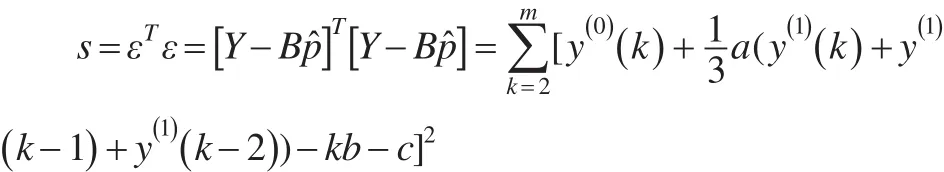
使s最小的参数a,b及c应满足:

即:
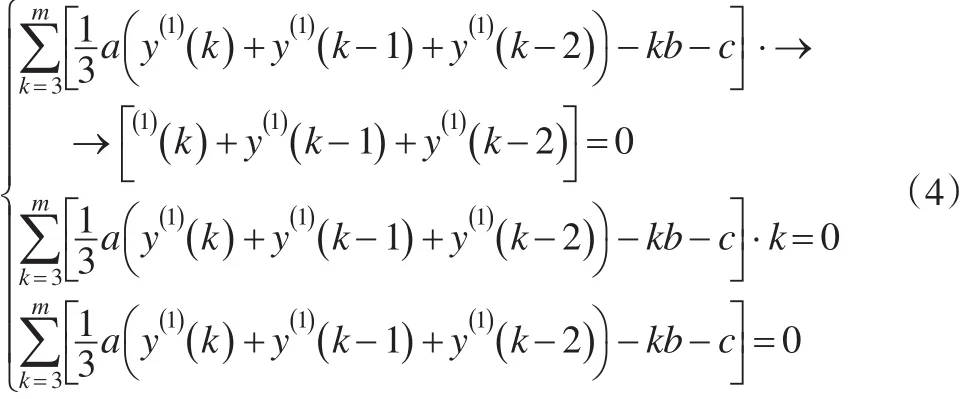
根据公式(4),可以做出如下推导:

即:
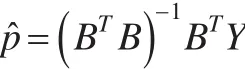
证明结束。
根据定义1可知:
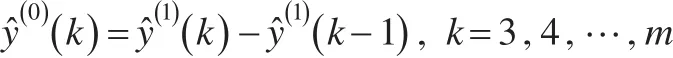
则:
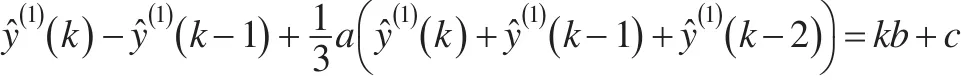
即:

整理公式(5),可得:
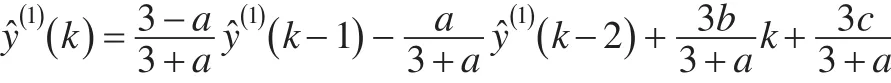
设:
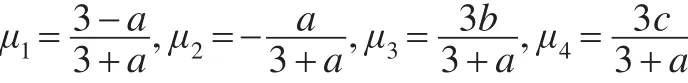
可得:
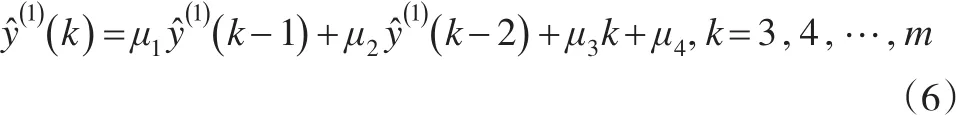
根据定义1可知,NGM3(1,1)模型的最终还原式可以表示为:
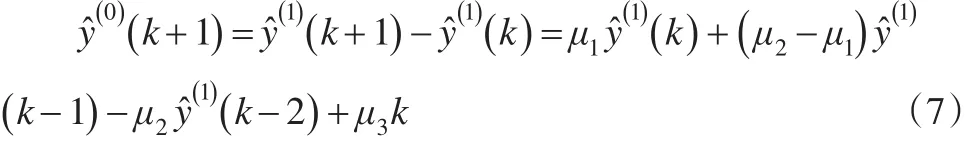
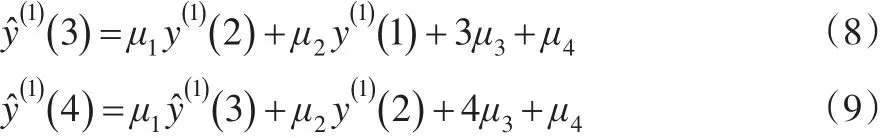
当k=3,4时,根据公式(6)可得:在公式(8)中,y(1)(1)及y(1)(2)=y(1)(1)+y(0)(2)分别称为NGM3(1,1)模型的初始值,视为已知数据。现根据公式(6),推导NGM3(1,1)模型的时间响应函数。
将公式(8)代入公式(9),整理得:

类似地,当k=5时,根据公式(6)可得:
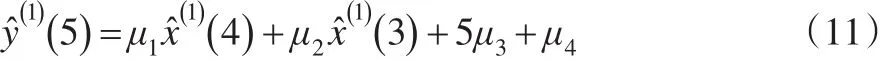
将公式(8)及公式(10)代入公式(11),可得:
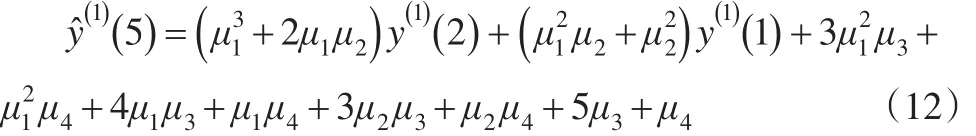
当k=5时:
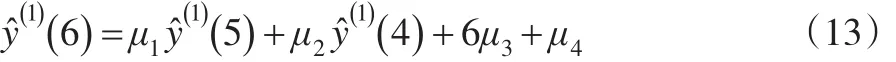
即:
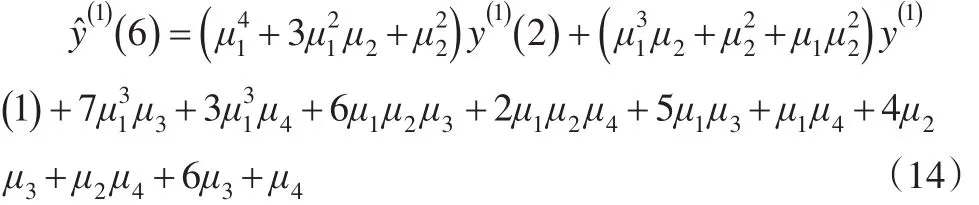
根据上文的推导过程可以发现,NGM3(1,1)模型时间响应函数的构成是非常复杂的,很难发现其递推规律。实际上,构建NGM3(1,1)模型的主要目的是模拟或预测数据(k)及y^(0)(k)。因此,NGM3(1,1)模型时间响应函数并非建模的必须环节。根据公式(7)可知,NGM3(1,1)模型满足递推算法,因此可以通过一段简单的递推程序来完成NGM3(1,1)模型的建模过程,实现NGM3(1,1)模型的模拟及预测功能。
相对于传统的灰色预测模型,NGM3(1,1)模型具有如下优点:
(1)NGM3(1,1)模型将背景值参数从两个拓展至三个,提高了灰色预测模型背景值的平滑效果,弱化了原始序列中的极端数据对灰色预测模型性能的影响。考虑到背景值的光滑度是影响灰色预测模型模拟及预测性能的重要因素,因此,理论上NGM3(1,1)模型性能优于传统的灰色预测模型。
(3)传统的灰色预测模型主要应用于小数据建模,随着样本量的增加,其预测性能往往变得更差。由于NGM3(1,1)模型背景值的光滑度优于传统的灰色预测模型,因此基于三参数的背景值构造方法对大样本数据具有更好的平滑效果,使得NGM3(1,1)模型能够模拟及预测更大样本量的应用场合,从而拓展传统灰色预测模型的适用范围。
2 模型比较与性能分析
为了测试模型性能,以文献[15]中的时序数据为基础,分别建立NGM3(1,1)模型、GM(1,1)模型及CNDGM(1,1)模型,计算这些模型的残差、相对模拟误差及平均相对模拟误差,并对上述模型的模拟性能进行比较。

表1 来自文献[15]的建模数据
根据表1中的数据建立灰色预测模型,模拟值及模拟误差如表2所示。表2中,模拟误差Δk及平均相对模拟误差的计算过程分为:
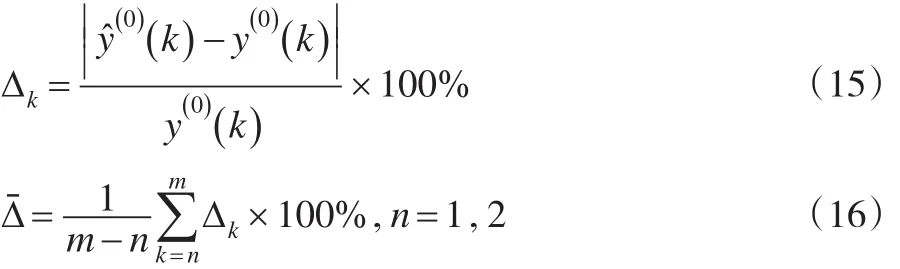
公式(16)用于计算灰色预测模型的平均相对模拟误差。由于初始值不是通过模型计算得到的,视为已知数据,在计算时应剔除。由于NGM3(1,1)模型具有与GM(1,1)模型及CNDGM(1,1)模型不同的初始值个数,因此对于GM(1,1)模型及CNDGM(1,1)模型,n=1;对于NGM3(1,1)模型,n=2,特此说明。

表2 NGM3(1,1)模型、GM(1,1)模型及CNDGM(1,1)模型的模拟值及模拟误差
从表2可以看出,本文所构建的NGM3(1,1)模型平均相对模拟误差为2.96%,精度等级接近I级,性能最优;其次为文献[15]提出的CNDGM(1,1)模型,其模型精度等级为II级;而传统的GM(1,1)模型精度最差。实例分析说明了NGM3(1,1)模型的背景值参数从两个增加至三个,能明显改善灰色预测模型背景值的平滑效果,进一步弱化了原始序列中的极端数据对灰色预测模型性能的影响,因此其模型性能优于传统的灰色预测模型。
3 基于NGM3(1,1)模型的预测实例
本文拟通过建立NGM3(1,1)模型,对三峡库区农村居民人均可支配收入进行了预测和分析。表3是2009—2016年三峡库区农村居民的人均可支配收入情况(数据来源于重庆市2009—2016年统计年鉴)。

表3 三峡库区2009—2016年农村居民人均可支配收入情况表 (单位:元)
根据表3可知,原始序列Y(0)=(y(0)(1),y(0)(2),y(0)(3),y(0)(4),y(0)(5),y(0)(6),y(0)(7) y(0)(8))=(21.62,22.83,23.74,23.89,24.50,26.88,27.66,26.31,32.44,37.67,39.50)
建立序列Y(0)的NGM3(1,1)模型,模型参数 μ1,μ2, μ3及μ4分 别 为 : μ1=1.0276; μ2=0.0138; μ3=667.3954; μ4=4234.6345
根据公式(7)可知,三峡库区农村居民可支配收入的NGM3(1,1)模型为:

公式(17)中,当 k=3,4,...,8时,y^(0)(k +1)为模拟数据;当 k=9,10,...时,y^(0)(k +1)为预测数据。根据公式(17),可以计算NGM3(1,1)模型的模拟值及模拟误差,如表4所示。为了比较NGM3(1,1)模型
的模拟性能,表4中同时列出了序列Y(0)的GM(1,1)模型及DGM(1,1)模型的模拟值及模拟误差。

表4 NGM3(1,1)模型、GM(1,1)模型及DGM(1,1)模型的模拟值及模拟误差
为了直观比较NGM3(1,1)模型、GM(1,1)模型及DGM(1,1)模型对三峡库区农村居民人均可支配收入的模拟性能,本文用MATLAB分别绘制上述三个模型的平均模拟相对差曲线图,如图1所示。
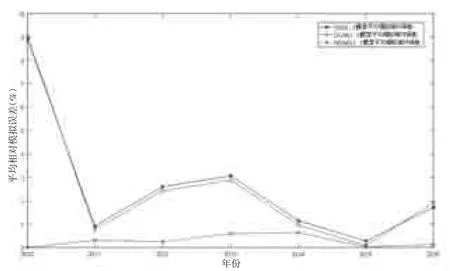
图1 NGM3(1,1)、GM(1,1)及DGM(1,1)的平均相对模拟误差对比图
根据图1不难发现,GM(1,1)模型及DGM(1,1)模型的平均相对模拟误差非常接近,前者略高于后者;而NGM3(1,1)模型的平均相对模拟误差具有绝对优势,远优于其他两个模型。研究结果表明本文所提出的灰色预测模型背景值构造新方法是合理有效的。
根据 公式(17),当 k=9,10,11,12,13,14,15,16,17,可以对2017—2025年三峡库区农村居民人均可支配收入进行预测,结果如表5所示。
根据表5不难发现,2025年三峡库区农村居民人均可支配收入预计将达到23614.18元,表明三峡库区农村居民人均可支配收入近些年来呈现快速增长的趋势。三峡库区经济社会取得了长足的发展,农村居民纯收入不断提高,缩小了与全国平均水平的差距。
4 结论
灰色预测模型背景值是影响灰色预测模型模拟及预测精度的重要参数。然而,现有灰色预测模型的构造或优化都是建立在参数x(1)(k -1)与x(1)(k)的基础之上,这导致灰色预测模型背景值容易受到建模序列中极端数据的影响,从而影响灰色预测模型性能的稳定性。为此,本文提出一种含三参数的灰色预测模型背景值构造的新方法,该方法提高了灰色预测模型背景值的平滑效果,弱化了原始序列中的极端数据对灰色预测模型性能的影响。通过案例比较,验证了基于三参数背景值的新型NGM3(1,1)模型的模拟性能优于传统以x(1)(k -1)及x(1)(k)为背景值基础的灰色预测模型。最后,将NGM3(1,1)模型应用于三峡库区农村居民可支配收入的模拟,模拟精度高达99.72%,进一步验证了三参数背景值构造新方法的可靠性及有效性。如何对以三参数为背景值的NGM3(1,1)模型进行进一步优化,是下一步的研究问题。

表5 三峡库区2017—2025年农村居民人均可支配收入情况表 (单位:元)
