基于耦合气动参数的HGV多模型估计

张凯， 熊家军， 付婷婷， 席秋实

(1. 空军预警学院 研究生大队， 武汉 430019； 2. 空军预警学院 预警情报系， 武汉 430019)

作为新一代跨大气层空天飞行器，高超声速滑翔目标(Hypersonic Gliding Vehicle, HGV)结合了航天器与航空器的特征，具有高速高机动、高精度、大航程等特点，可实施远距离机动快速打击[1-2]。随着美国分别于2011年和2017年成功试射陆基和潜射型高超声速滑翔弹头(AHW和IRCPS)，标志着HGV武器已初步具备作战能力，这给中国空天安全带来了巨大威胁。面对这类目标早期预警和拦截中的目标跟踪问题，有必要结合HGV的动力学特性进一步研究相关理论。

不同于传统高速目标，HGV沿非惯性弹道机动飞行，地基传感器存在探测时间短、测量精度低等问题，使用传统跟踪算法难以对HGV实现准确跟踪。从滤波器应用角度来看HGV跟踪是典型的非线性滤波问题，其估计性能很大程度上取决于目标状态模型的精细程度。一般来说，合理构建机动目标的高阶状态模型有助于提高估计精度。根据目标状态建模思想的不同，方法大体可分为2类：①对目标未知加速度或加加速度建模[3-4]，构建CA、Singer和Jerk等运动学模型，这种方法通用性较强，具有较快的机动响应能力，但估计精度有限；②对目标未知气动力建模[5]，通过状态增广[6-9]或输入估计[10-12]等方法构建动力学模型，这种方法物理含义清晰，稳定跟踪时估计精度高，广泛应用于机动再入目标跟踪。缺点是当气动力变化较快或模型不够准确时，跟踪精度会大幅下降。由于HGV运动形式复杂，单一运动模型难以准确刻画其运动特征，交互多模型(Interacting Multiple Model, IMM)方法可以较好地表现HGV的复杂机动[8-9,12-13]。然而，在面对状态维度大、传感器采样率高的HGV估计问题时，IMM往往会大幅增加了运算负担。

据以上分析可知，对未知气动力准确建模是提高HGV跟踪精度的有效途径。同时，IMM方法可以显著改善模型匹配程度，但如何调和模型集覆盖能力与计算量之间的矛盾是亟需解决的问题。为此，本文首先论证气动加速度建模的必要性，将气动加速度在转弯和俯仰方向存在的耦合信息引入气动参数模型，构建滚转(Bank)和螺旋(Sprial)模型。然后，综合考虑估计精度和实时性的需求，使用一种目标状态与气动参数分离估计的模型替代传统的状态增广模型，并对大幅变化的参数对应的机动频率进行IMM建模。最后，对不同条件下的多种模型跟踪算法进行仿真验证。

1 目标气动加速度分析

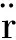
(1)

式中：aA为气动加速度，是造成目标机动的原因；aG为重力加速度。

从式(1)中可以看出，目标在重力加速度aG作用下，运动方式表现为惯性弹道再入运动；在aA各向分量的作用下，目标具有非惯性的跳跃再入和横向机动能力。为从动力学角度理解aA的变化规律，将aA在位于目标质心的半速度(Velocity-Turn-Climb, VTC)坐标系中分解[5]：

aA=-Duv+L(-utsinφ+uccosφ)

(2)

式中：uv、ut和uc为VTC坐标系中各坐标轴的单位矢量;φ为滚转角；D和L分别为阻力加速度和升力加速度，其表达式为

其中：m为质量；ρ为大气密度；v和S分别为目标速度和等效截面积；α为迎角，φ和α为HGV的控制变量；CD(α)和CL(α)分别为阻力系数和升力系数，为α的函数。

从式(2)可以看出，HGV通过调整φ和α，使aA各向分量发生变化从而实现各种复杂机动。为进一步分析aA对目标运动状态的影响，对aA进行求导，则有[14]

(3)

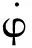
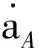
2 耦合气动参数建模

2.1 气动参数定义

HGV机动是由目标的控制变量变化决定的。据式(2)可知，即使φ和α不发生变化，由于目标跳跃飞行的原因，大气密度ρ剧烈变化，气动加速度aA的各向分量会大幅波动。因此，直接对气动加速度建模会造成aA的变化规律难以刻画。利用已知的状态依赖参量ρv2/2将气动加速度aA中的未知参数(CD(α)、CL(α)、S、m和φ)转化为气动参数αP=[αv,αt,αc]T是一种流行的建模做法[5]。参照文献[5]建立气动加速度aA与气动参数αP的关系式为

(4)

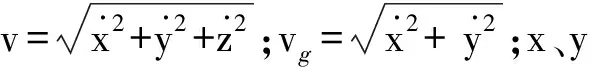
气动参数αP与大气密度ρ变化无关，可以直接表征目标的各向机动：αt>0和αt<0分别对应目标水平左转和右转机动；αc>0和αc<0分别对应目标爬升和俯冲机动。利用气动参数α取代气动加速度aA表示目标的未知机动输入，可以直接从目标机动特点出发调整模型参数，有助于提高估计精度。然而，αP=[αv,αt,αc]T本质上是对气动加速度aA的解耦处理，分析式(2)可知，aA在转弯和俯仰方向存在明显的耦合关系。为有效利用这一耦合关系以提高建模精度，2.2节和2.3节将其作为先验信息引入气动参数αP表达式中，分别建立Bank和Spiral模型。

2.2 Bank模型

联立式(2)和式(4)，可得气动参数αP与控制变量α、φ之间的关系式为

(5)

从式(5)中不难看出滚转角φ通过改变CL(α)S/m在纵向平面的指向实现目标机动，表现为转弯力参数αt和爬升力参数αc的非线性负相关：

(6)

(7)

气动参数αB从动力学的角度表征了目标的控制规律，具有清晰的物理意义：αv和α1对应阻力和升力的大小，φ表示升力的方向。通过这种形式的参数建模，αB考虑了αt和αc之间的耦合关系，但本质上与αP同阶，并未增加计算复杂度。联立式(4)和式(7)，可利用αB表示气动加速度aA为

(8)

采用一阶马尔可夫模型表示各参数的机动特性，气动参数αB的系统模型可表达为

(9)

式中：wv、wl和wφ分别为对应参数的过程噪声；λv、λl和λφ分别为对应参数的机动频率。HGV飞行过程中，α主要起到维持目标稳定飞行的作用，α频繁调整容易造成目标气动热急剧增大甚至飞行失稳，一般取为常值或小区间变化[15]。同时，研究表明短时间内CD(α)和CL(α)随α呈现近似线性变化[16-17]。因此，λv和λl可取为较小的值。同时，作为目标机动的主要控制变量，滚转角φ决定了升力在转弯和爬升方向分量的大小，变化较为频繁，λφ可取为较大的值。

2.3 Spiral模型

与Bank模型思想类似，Spiral模型也考虑了αt和αc之间的耦合关系。根据式(5)分别对αt和αc求导，则有

(10)

可知αt和αc可组成一个稳定的谐波振荡器[6]

(11)

式中:ϖ为滚转角φ的角加速度，反映了滚转角φ变化的剧烈程度。将ϖ增广到气动参数αP中，可得改进的气动参数向量为αS=[αv,αt,αc,ϖ]T。不难看出，αS利用αv、αt和αc表征了目标在VTC坐标系中各向的机动，利用ϖ表征了αt和αc之间的耦合关系，ϖ本质上是αP的一阶导数信息。

Spiral模型的气动加速度aA表达式与式(4)保持一致。采用一阶马尔可夫模型表示ϖ的机动特性，气动参数αS的系统模型可表达为

(12)

式中：wt、wc和wϖ分别为对应参数的过程噪声；λϖ为ϖ对应的机动频率。由于ϖ变化是目标机动的主要影响，λϖ可取为较大的值。

3 IMM分离估计算法

3.1 分离估计模型

基于气动参数建模的跟踪算法通常将气动参数增广到状态模型进行滤波计算，但这种算法在多模型条件下会显著增加计算复杂度。考虑到需要对气动参数进行多模型假设，本文使用一种状态量与气动参数分离估计模型替代增广模型，可有效降低计算复杂度[18]。

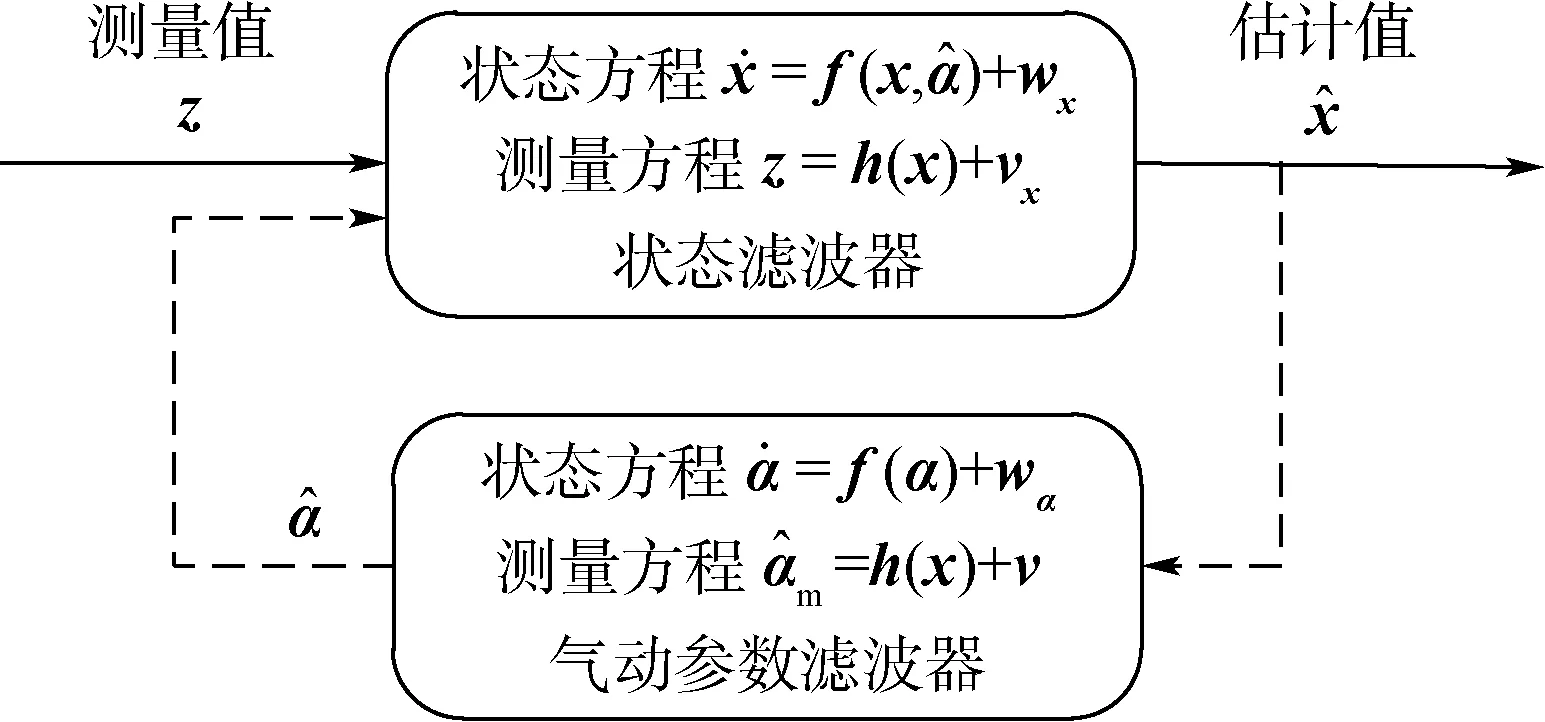
图1 分离估计模型结构Fig.1 Structure of decomposed estimation model

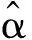
3.2 滤波器描述

3.2.1 状态滤波器

ENU坐标系下HGV状态方程的离散化表达式为

x(k+1)=Fxx(k)+

G[aA(k)+aG(k)]+wx(k)

(13)

式中：

(14)

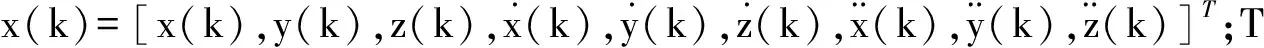
(15)

其中：Re为地球半径。

在球坐标系中建立量测方程，目标的量测值为z(k)=[R(k),A(k),E(k)]T，R(k)、A(k)和E(k)分别为观测的径向距离、俯仰角和方位角。根据ENU坐标系和球坐标系的转换关系，目标的量测方程可表达为

z(k+1)=h[x(k+1)]+vx(k+1)=

(16)

式中:vx为状态滤波器的量测噪声;nR(k+1)、nA(k+1)和nE(k+1)为各量测值对应的量测噪声。状态滤波器的过程噪声Qx(k)与量测噪声Rx(k)参考文献[19]。

3.2.2 Bank参数滤波器

对式(9)离散化，可得Bank参数滤波器状态模型的表达式为

(17)

(18)

(19)

(20)

利用状态滤波器得到的状态误差协方差Px(k)求解量测误差协方差RB(k+1)为

RB(k+1)=diag(rB1,rB2,rB3)

(21)

式中:

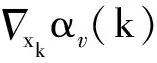
3.2.3 Spiral参数滤波器

对式(12)离散化，可得Spiral参数滤波器状态模型表达式为

(22)

(23)

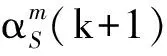
vS(k+1)

(24)

根据状态滤波器得到的状态误差协方差Px(k)求解量测误差协方差Rs(k+1)为

Rs(k+1)=diag(rS1,rS2,rS3,rS4)

(25)

式中:

式中：σϖ为ϖ对应的量测误差协防差。

3.3 IMM设计

基于气动参数建模的跟踪算法的共性缺点是大多都基于某种单一的假设模型，一旦在跟踪过程中目标轨迹和设定的模型不匹配，或者气动参数变化导致加速度状态突变时，状态估计精度就会迅速恶化。当前普遍认为IMM是解决此类问题的有效途径。

在气动参数系统模型式(17)和式(22)中，气动参数时间序列相关性的表现为机动频率λ的大小，其取值决定了HGV机动时的状态估计精度[8]。当目标稳定飞行时，量级为10-4s-1的λ可表现参数的缓变特性；对于目标机动飞行的情况，气动参数瞬时变化较大，量级为0.1～1 s-1的λ可表现参数的突变特性。同时，在飞行过程中HGV的机动模式可能介于缓变和突变之间任意模式。为此，可利用多个机动频率λ组成的IMM模型提高模型匹配程度。为调和机动模式的覆盖需求与计算复杂度的矛盾，本文结合上述取值范围，对Bank模型的φ和Spiral模型的ϖ对应的机动频率λφ和λϖ进行适当选取。如图2所示，设计的IMM模型由设置r个不同机动频率λi(i=1,2,…,r)的滤波器组成。

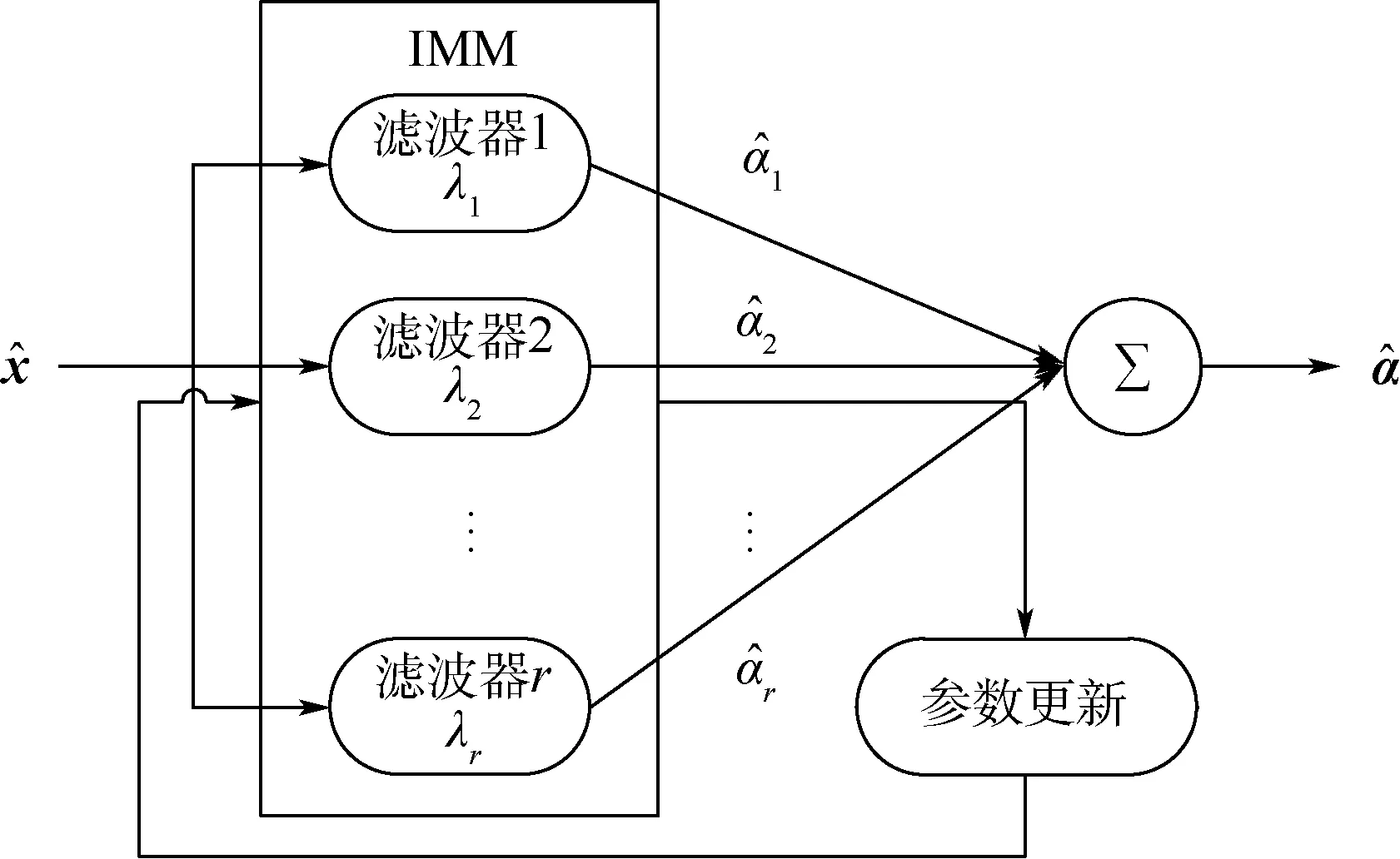
图2 气动参数IMM示意图Fig.2 IMM schematic of aerodynamic parameter

4 仿真分析

为验证本文方法可行性，设计如下仿真环境：①目标参数：HGV模型参考美国洛马公司CAV-H的基本参数[20]，飞行器总长约为4 m，质量1.7 t，初始高度45 km，速度为4 000 m/s，采用三自由度动力学方程积分生成仿真弹道，采用标准制导法控制φ和α变化实现机动[15]；②传感器参数：采用扩展卡尔曼滤波(EKF)滤波器，距离量测标准差为500 m，方位角、俯仰角量测标准差均为0.01 rad，Bank模型和Spiral模型中r取值均为3，对应的机动频率取值分别为0.001、0.01和0.5 s-1。为检验算法性能，对仿真算例进行500次蒙特卡罗仿真，分别计算均方根误差(Root Mean Square Error, RMSE)。

4.1 不同模型条件下估计性能仿真

利用2类模型跟踪算法进行仿真对比：①运动学模型：CA、Singer和Jerk模型；②动力学模型：基于气动参数αP=[αv,αt,αc]T增广的机动载入飞行器(MaRV)模型、本文Bank模型和Spiral模型。需要注意的是，为保证仿真合理性，仿真中的6个模型均为单模型，即不考虑IMM情况。

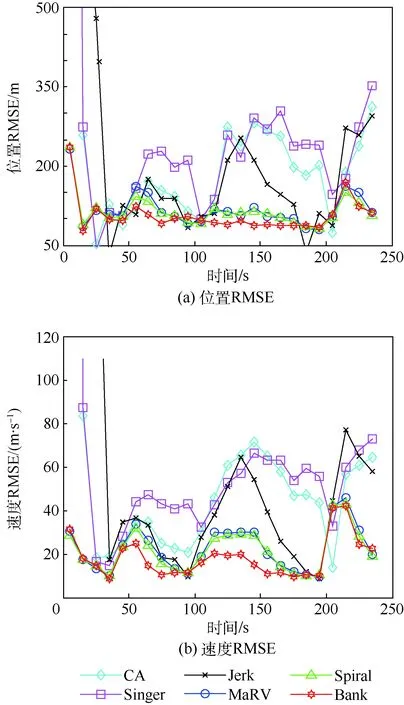
图3 不同模型位置和速度估计RMSEFig.3 RMSE in position and velocity estimate of different models

图3给出6种模型位置与速度RMSE仿真结果。不难看出：①当目标发生机动时(气动参数变化)，各模型的位置和速度跟踪误差发生显著增大，然后逐渐减小；②动力学模型跟踪误差收敛较快，显著小于运动学模型，表现出较好的跟踪精度；③在动力学模型中，Bank模型性能优于其他2种模型，Spiral模型略微优于MaRV模型，但差别不大。

4.2 不同动力学模型条件下IMM估计性能仿真

为分析气动参数估计性能，对不同动力学模型条件下IMM算法进行仿真，MaRV模型的机动频率参考第4节仿真环境数据。图4和图5分别给出3种动力学模型气动参数估计值以及相应的RMSE仿真结果。其中，Bank模型的αt和αc的估计值是利用式(7)间接计算得到。从图4和图5中可以看出：①在当气动参数剧烈变化时，不同动力学模型对气动参数的估计均发生时延，估计误差逐渐增大，且难以快速收敛，说明动力学模型难以精确估计气动参数；②MaRV模型与Spiral模型对气动参数的估计误差量级相当，而Bank模型的估计精度则优于上述2种动力学模型。

图4 不同动力学模型气动参数估计值Fig.4 Aerodynamic parameter estimation values of different dynamic models

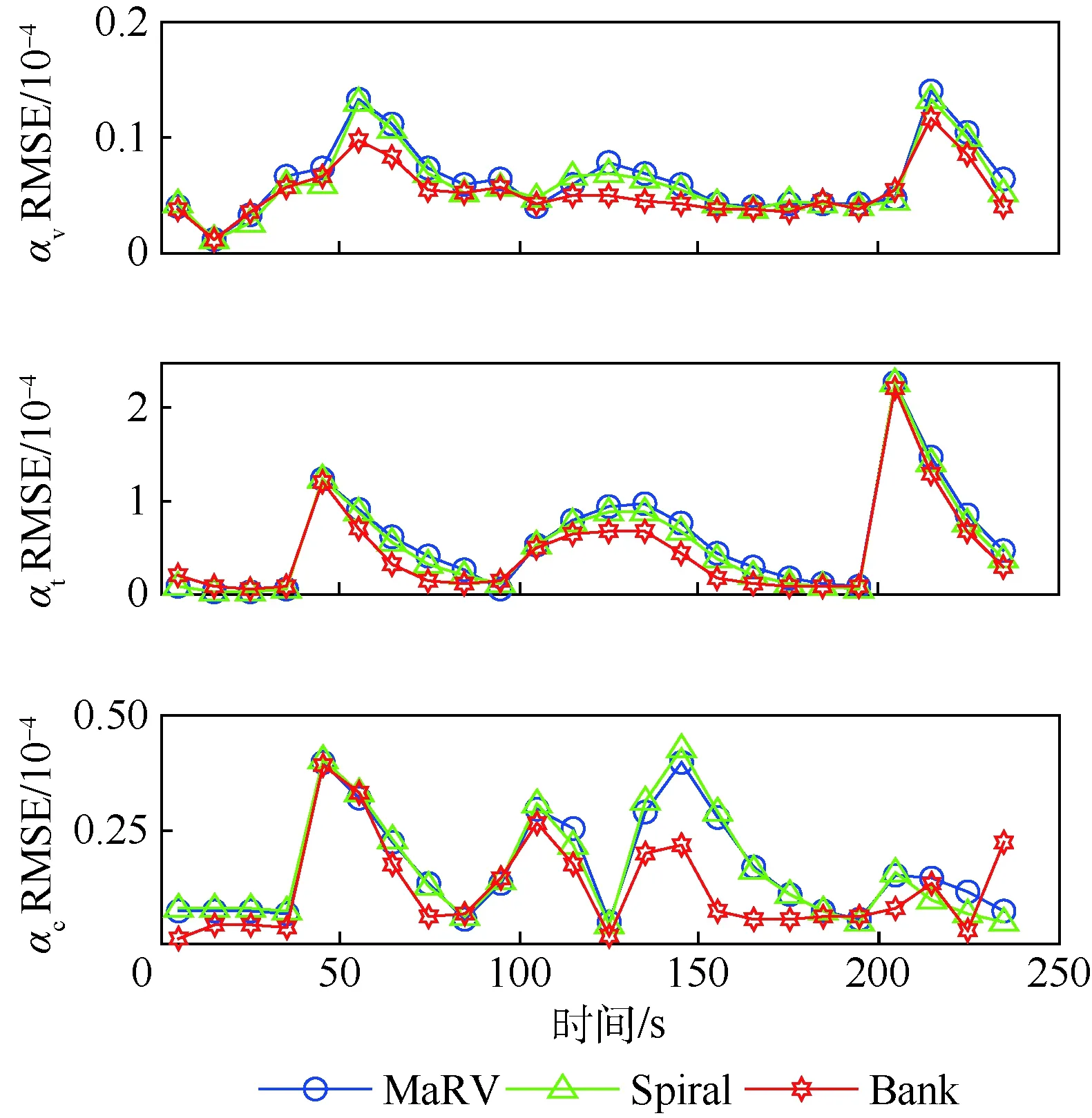
图5 不同动力学模型气动参数估计RMSEFig.5 RMSE in aerodynamic parameter estimate of different dynamic models

对动力学模型仿真结果的原因进行分析：①MaRV模型未考虑各向气动参数耦合的先验信息，是一种相对“宽松”的解耦模型，导致估计性能下降；②Spiral模型中ϖ本质上是加速度的一阶导数信息，状态滤波器无法提供关于ϖ的先验信息，其仅能通过Spiral参数滤波器间接辨识，导致ϖ估计精度有限；③Bank模型中αB本质上加速度同阶，因此利用状态滤波器计算得到αB的伪量测值，由于考虑了气动参数耦合信息，Bank模型能够有效提高估计精度。

4.3 不同滤波器参数条件下IMM估计性能仿真

为检验不同滤波器参数对本文所提动力学跟踪算法的影响，利用表1中6个算例从滤波算法、噪声方差和采样周期对模型性能进行分析。

利用算例1和2对不同滤波算法下动力学模型进行性能仿真，如图6所示为位置与速度RMSE仿真结果。不难看出，无迹卡尔曼滤波(UKF)的估计精度虽然高于EKF，但相对于动力学模型对估计精度的提升，滤波算法的优势并不明显。可见，模型的精细程度对跟踪算法影响更大。

利用算例1和算例3～6对不同量测参数条件下的动力学模型进行性能仿真，如表2所示为位置、速度和气动参数的RMSE均值对比情况。可以看出：①随着量测噪声方差增大或减小，各状态量RMSE均值均随之增大，但气动参数估计误差变化更为剧烈，可见量测噪声对气动参数估计影响较大；②随着采样周期增大或减小，各状态量RMSE均值随之增大或减小，但位置与速度估计误差变化更为剧烈，可见采样周期对位置与速度估计影响较大。

分析以上仿真结果可以得出以下结论：①滤波算法对不同动力学模型跟踪算法性能影响有限，采用EKF可有效提高计算效率；②传感器的噪声方差大小直接影响了算法对目标状态的估计精度；③调和气动参数辨识精度与计算复杂度的矛盾，应当合理选择采样周期；④虽然滤波算法和和量测参数的变化使模型性能发生了改变，但总体上Bank性能优于Spiral模型，Spiral模型略微优于MaRV模型，进一步证实了4.1节和4.2节的结论。

表1 性能对比算例参数设置

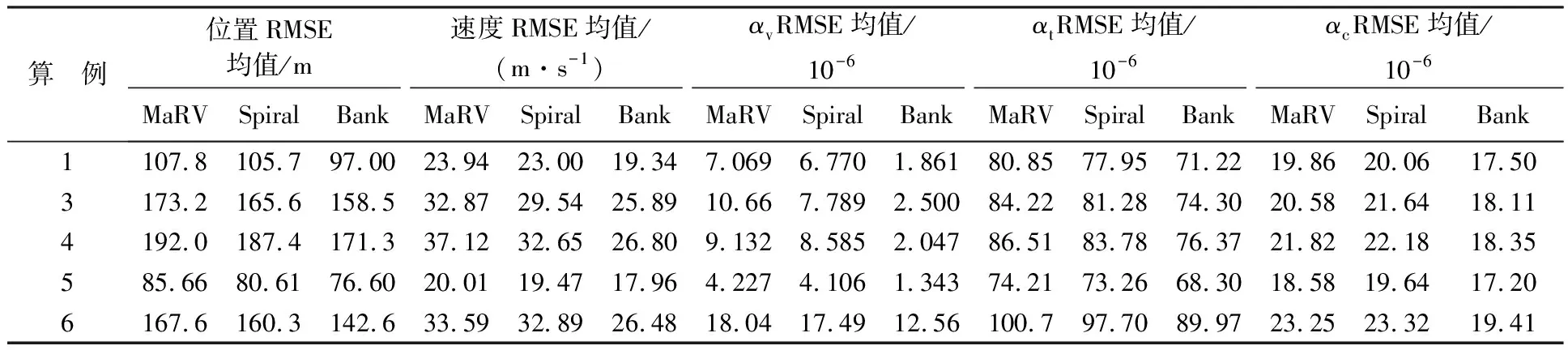
算 例位置RMSE均值/m速度RMSE均值/ (m·s-1)αvRMSE均值/10-6αtRMSE均值/10-6αcRMSE均值/10-6MaRVSpiralBankMaRVSpiralBankMaRVSpiralBankMaRVSpiralBankMaRVSpiralBank1107.8105.797.0023.9423.0019.347.0696.7701.86180.8577.9571.2219.8620.0617.503173.2165.6158.532.8729.5425.8910.667.7892.50084.2281.2874.3020.5821.6418.114192.0187.4171.337.1232.6526.809.1328.5852.04786.5183.7876.3721.8222.1818.35585.6680.6176.6020.0119.4717.964.2274.1061.34374.2173.2668.3018.5819.6417.206167.6160.3142.633.5932.8926.4818.0417.4912.56100.797.7089.9723.2523.3219.41

5 结 论

1) 对HGV的加速度导数项进行了推导和分析，得出机动的实质是气动加速度改变引起目标质心运动和绕质心运动变化的结论。为改善算法估计精度，应对目标的高阶状态进行建模。

2) 在非耦合气动参数建模的基础上，将气动参数在转弯和俯仰方向存在的耦合关系作为先验信息，构建了Bank和Spiral模型。

3) 针对多模型条件下增广模型导致计算复杂度增加的问题，使用一种由状态滤波器和气动参数滤波器组成的分离估计模型替代增广模型。同时，对模型中变化较大的参数进行机动频率IMM建模，提高了模型匹配程度。

4) 仿真结果表明，动力学模型性能显著优于运动学模型。同时，在不同条件下对比3种动力学模型可知，本文所提的2种模型对位置、速度和气动参数的估计精度好于MaRV模型，Bank模型显著优于Spiral模型，且计算复杂度更小。下一步将继续深入研究HGV动力学特性，以期构建更加精细的动力学模型，进一步改善估计精度。