基于信息熵和粗糙集的空中目标威胁评估方法
2018-10-30杨远志周中良刘宏强寇添范翔宇
杨远志, 周中良,*, 刘宏强, 寇添, 范翔宇
(1. 空军工程大学 航空工程学院, 西安 710038; 2. 空军工程大学 装备管理与安全工程学院, 西安 710051)
空中目标威胁评估是地面防空系统进行武器配置和资源管理的基础,对于提高防空系统多目标攻击和生存能力具有极其重要的价值[1]。
空中目标威胁评估是典型的多属性决策问题,根据空中目标对地面防空系统产生威胁的各影响因素,建立科学、合理的威胁评估模型,并求解各目标威胁等级[2]。目前,相关领域学者对于威胁评估的研究已经取得了丰硕的成果:文献[3]基于灰色系统理论改进了威胁评估中的指标权重计算方法,构建威胁评估模型并计算威胁等级;文献[4]针对静态评估无法与实战相结合的问题,将直觉模糊熵与动态直觉模糊方法相结合,确定目标树典型矩阵并对目标属性进行赋权,建立动态多目标威胁评估模型;文献[5]将层次分析法和主成分分析方法相结合,确定目标属性权重,建立威胁评估模型;文献[6]利用相邻指标相对重要性模糊标度值确定评估指标的权重系数,基于遗传算法建立了威胁评估模型,克服局部收敛问题,实现空战态势的有效评估;文献[7]针对指标中存在的模糊不确定性信息问题,提出采用区间数的方法建立多目标威胁评估模型;文献[8]在多目标威胁评估的基础上,采用神经网络方法对多目标协同分配攻击进行建模,实现对多目标的合理评估和分配;文献[9]采用支持向量机方法得到评估指标与威胁度之间的非线性量化关系,量化目标威胁程度。上述方法均可实现对多目标的威胁评估,但灰色理论、模糊理论和层次分析法等均存在人为主观因素的影响,神经网络和支持向量机等方法需要大量的先验信息作为训练样本,难以满足防空作战的需要。
针对上述方法存在的不足,本文融合信息熵(Information Entropy,IE)方法与粗糙集(Rough Set,RS)理论对空中目标威胁程度进行定量评估。粗糙集理论不需要先验知识,能够处理不完备、不精确信息,具有一定的容错性和实效性,且该方法基于数据驱动,能够消除数据冗余,提取决策规则,规避人为主观因素的影响[10]。但是在信息系统缺少决策属性时,经典粗糙集理论无法对其进行处理,因此本文提出利用信息熵方法选取权重最大的属性来替代决策属性,构造粗糙集理论可以处理的信息系统,解决粗糙集理论在处理无决策属性问题时的短板,寻找一种新的空中目标威胁评估方法。
1 基于信息熵的目标属性权重计算
信息熵由Shannon[11]于1948年提出,是信息论中信息无序程度的度量。某属性信息熵越大,信息无序度越高,信息量越小,其在评价中的权重越小,因此信息熵可用于评估系统中属性权重的大小。
本文借鉴信息熵方法,计算各目标属性的信息熵和权重,确定权重最大的属性来替代决策属性,为构建粗糙集理论评估模型建立基础。
1.1 目标属性的确定
根据攻防双方实际作战态势,从空中目标的角度出发,综合考虑影响目标威胁程度的作战参数和性能指标,选取目标的类型、速度、高度、距离、航向角及干扰能力作为评估指标[9,12]。
1.2 属性权重的计算
信息熵计算各属性权重的具体步骤如下[13]:
步骤1构造决策矩阵。
假设有m个空中目标,n个目标属性,根据原始样本数据构造决策矩阵C=(cij)m×n。其中cij为第i组数据关于第j个属性的值。
步骤2计算特征值矩阵。
求取矩阵C的特征值,并将对应的特征值向量组成特征值矩阵:
(1)
步骤3特征值矩阵规范化。
对λ矩阵进行规范化处理,消除空中目标不同属性之间的量纲差异。此步骤需要判定λ矩阵中各属性的性质,划分效益型和成本型,从而得到规范化特征值矩阵R=(rij)m×n。
其中,效益型是指其值越大,威胁程度越大,计算公式为
(2)
成本型是指其值越大,威胁程度越小,计算公式为
(3)
步骤4矩阵R归一化。
对矩阵R的每一列进行归一化处理,得到
(4)
式中:
(5)
步骤5计算属性信息熵。
利用式(6)计算属性cj的信息熵:
(6)
步骤6得到权重向量。
通过各属性的信息熵可以得到各属性权重并组成权重向量:
ω=(ω1,ω2,…,ωn)
(7)
式中:
(8)
1.3 确定权重最大的属性替代决策属性
取属性权重向量ω=(ω1,ω2,…,ωn)中最大的权重值记为ω0:
ω0=max{ωj}j=1,2,…,n
(9)
与ω0相对应的目标属性即可作为决策属性,将此决策属性和其他条件属性联合,构造粗糙集理论可以处理的威胁评估模型。
2 基于粗糙集的目标威胁评估
粗糙集理论可以在保持分类能力不变的情况下,通过数据挖掘和知识发现,实现对数据规律的探寻,从而实现对评估问题的求解。本文通过信息熵方法选取目标属性替代决策属性,构建完整的粗糙集理论威胁评估模型。
2.1 构建决策环境
粗糙集理论定义{U,A,F,D}为决策信息系统。其中,U={x1,x2,…,xn}为评估对象的集合;A={a1,a2,…,am}为条件属性的集合;F={fl:U→Vl(l≤m)}为U与A之间的关系集,Vl为al(l≤m)的值域;D:U→VD为决策。
2.2 离散属性值
采用属性重要性的离散化方法,将原始数据转化为粗糙集可以处理的数据类型,主要步骤如下[14]:
步骤1选取初始种群,并对其进行初始化处理pop(G),G=1。

(10)
Z在A中的重要性:
EZ(Y)=rA(Y)-rA/Z(Y)
(11)
计算各个体的适应度fitness(i)及适应度的和sum(G)。
步骤3选择操作:轮盘赌选择法在每轮中生成一个[0,1]的均匀随机数,选择累计概率与该随机数最接近的个体作为下一代的个体。杂交操作:随机选取杂交点产生随机数,确定杂交次数及参与杂交的父辈个体,对杂交点后的部分子串进行交换,产生下一代个体。变异操作:随机选取变异个体,确定变异断点,若原为1,则变异为0,反之为1。
步骤4统计所有个体,删除重复项。
步骤5终止条件sum(G)/total(G)>1-ε,ε为给定的小正数,若满足,则结束;否则,G=G+1,返回步骤2。
2.3 属性约简
基于决策辨识矩阵[10]的属性约简方法如下:
步骤1构造决策辨识矩阵。
称{U,A,F,D}为决策信息系统,记为
(12)
则Dd([xi]A,[xj]A)为[xi]A与[xj]A的决策辨识集,称式(13)为决策辨识矩阵:
Dd=(Dd([xi]A,[xj]A)|[xi]A,[xj]A∈U/RA)
(13)
式中:RA为U上的等价关系。
步骤2构造决策约简集。
若B为决策协调集,∀Dd([xi]A,[xj]A)≠∅,有
B∩Dd([xi]A,[xj]A)≠∅
(14)
∀C⊂B都不为决策协调集,称B为决策约简集。
2.4 计算属性指标下的决策属性的权重表
称{U,A,F,D}是决策信息系统,每个属性子集a⊆A决定了一个不可区分的关系ind(a):
ind(a)={(x,y)∈U*U|∀a∈A,a(x)=a(y)}
(15)
关系ind(a)构成了U的一个分类。
通过对条件属性和决策属性的分类,定义相似度:
(16)

结合信息熵求得的属性权重向量,可以得到指标Q用于评估目标威胁程度:
(17)
将指标Q进行排序,可得到对空中目标的威胁程度排序结果。
3 威胁评估处理流程
将信息熵方法与粗糙集理论相结合,用以构建对空中目标进行威胁评估的方法模型(见图1)。
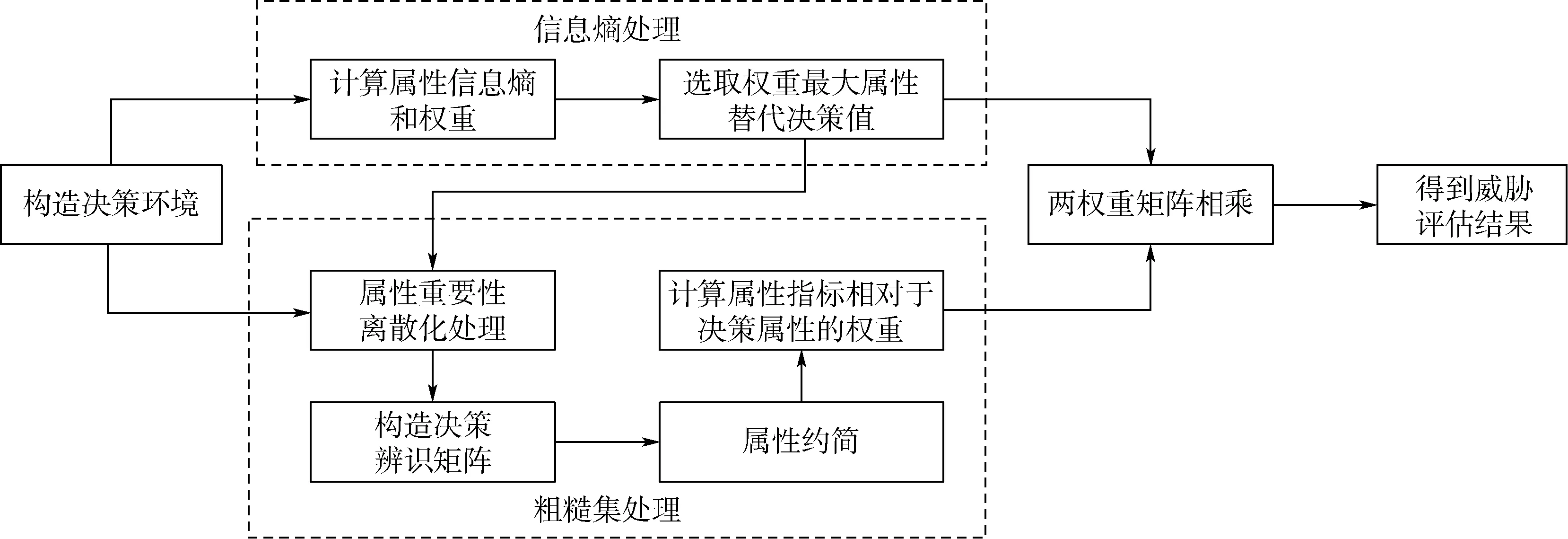
图1 威胁评估模型Fig.1 Model of threat evaluation
地面防空系统将侦收到的空中目标信息用以构建粗糙集处理的决策环境,通过信息熵弥补其无法处理无决策属性信息系统的不足,实现对空中目标的威胁评估,整个评估流程可以分为2个模块。一是信息熵处理模块,采用信息熵方法计算各属性的信息熵和权重,选取权重最大的属性替代决策属性并得到权重向量。二是粗糙集处理模块,将得到的决策属性与目标属性用以构建决策信息系统,按照属性重要性的步骤离散决策信息表,得到核心属性并进行属性约简,计算各属性指标下决策属性的权重值。最后,将两模块输出结果进行处理,得到评估目标威胁程度的指标Q,对指标进行排序,即可得到各目标的威胁程度。
4 仿真分析
提取文献[12]仿真部分的6组典型数据并去除其决策属性,作为本文的样本数据,构建已知方案集(即初始信息表),按照本文IE-RS模型进行空中目标威胁度量值的评估运算,对比评估运算结果,从而验证本文模型的可行性和有效性。为表示方便,将目标类型、目标速度、目标航向角、目标干扰能力、目标高度、目标距离6个目标属性依次简记为a1、a2、a3、a4、a5、a6。
表1中,a1、a4、a5为定性指标,需要对其进行量化处理以适应粗糙集理论的数据需求方式。对此,本文做出如下量化规则[9,15]:
1) 目标类型:小型目标(如巡航导弹)、大型目标(如轰炸机)、直升机依次量化为3、2、1。
2) 目标干扰能力:强、中、弱、无依次量化为4、3、2、1。
3) 目标高度:高、中、低、超低依次量化为4、3、2、1。
可以得到如表2所示的量化数据,作为本文模型处理的初始信息表。
对各目标属性进行分析,可以得到如下结论:a1、a2、a4为效益型属性;a3、a5、a6为成本型属性。利用式(1)求取特征值矩阵,式(2)~ 式(4)实施归一化处理,得到如表3所示的归一化决策矩阵。

表1 目标威胁数据库数据
通过式(6)~ 式(8)计算得到各属性的权重(见表4)。
从表4的属性权重可以看出a5的权重最大。因此,可以将a5作为决策属性D,构造完备的信息决策表,并对各属性进行离散化处理,得到如表5所示的完备离散化数据。
结合式(12)~ 式(13)得到如表6所示的决策辨识矩阵。
表2初始信息表
Table2Initialinformation

目 标a1a2/(m·s-1)a3/(°)a4a5a6/mt1250013044360t225509033160t336005034160t4375015031400t518814011320t619018022170
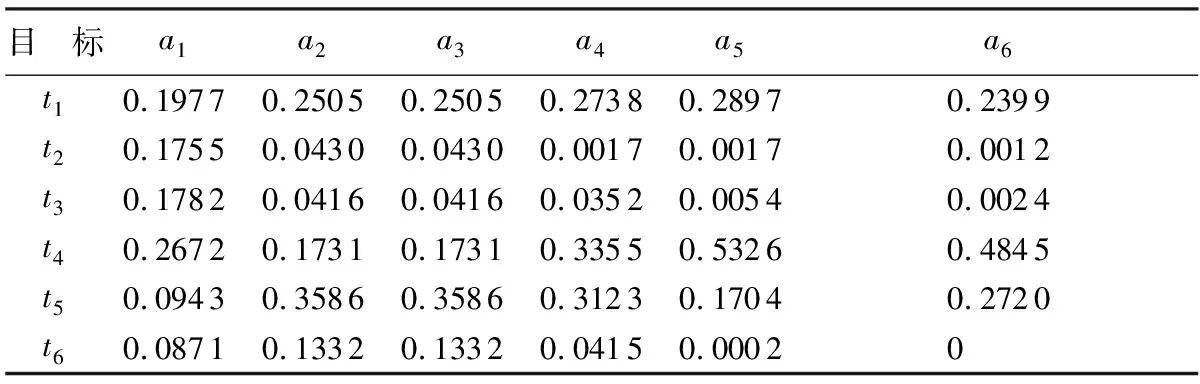
表3 归一化决策矩阵

表4 各属性权重
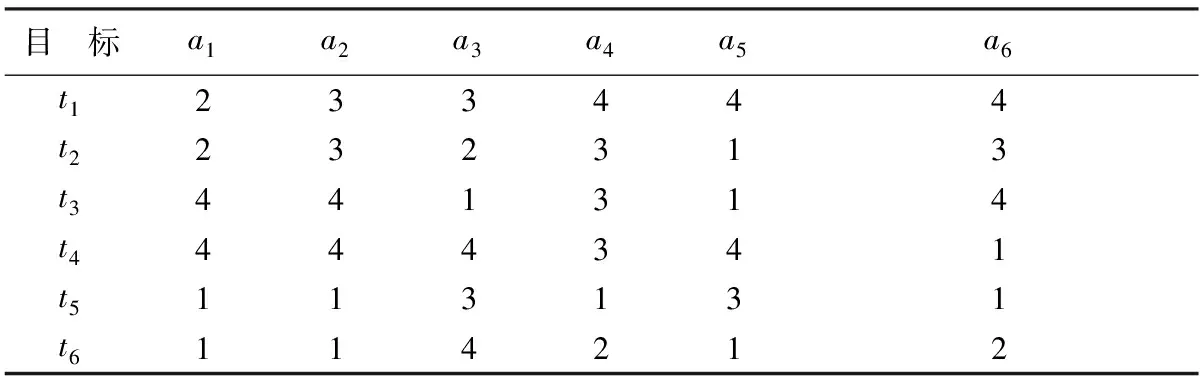
表5 离散化数据
依据式(14)对表6进行约简,得到系统的核心属性为a1;相对必要属性为a3、a6,约简后的决策系统如表7所示。
结合式(15)计算目标对条件属性和决策属性的分类:
U/a1={t1,t2},{t3,t4},{t5,t6}
U/a3={t1,t5},t2,t3,{t4,t6}
U/a6={t1,t2,t3},t4,{t5,t6}
U/D={t1,t3},t2,{t4,t5},t6

表6 决策辨识矩阵
通过式(16)计算得到各属性指标下的决策属性的权重如表8所示。
最终由式(17)得到各个目标的威胁度量值Q(见表9)。
将本文仿真结果与文献[12]样本数据的威胁值进行对比(见图2)。
将表9中IE-RS模型得到的各目标威胁度量值进行排序,可以得到空中目标威胁程度为t4>t3=t2>t1=t5>t6,将排序结果与文献[12]中的目标威胁原始样本决策进行对比,可以发现其变化规律趋于一致,验证了本文模型仿真结果的正确性,说明采用信息熵方法选取权重最大的属性替代决策属性是可行和有效的,可以较好地判定空中目标的威胁程度,解决在决策属性未知情况下的空中目标威胁评估问题,拓宽粗糙集理论进行评估的适用范围。同时,粗糙集理论基于数据驱动,降低对先验信息的需求和人为主观因素的影响,为构建科学、合理的威胁评估模型提出一种新的工程决策方法。模型可为后续的武器配置和资源管理提供支撑,可作为后续电子对抗或火力打击决策时的理论依据。
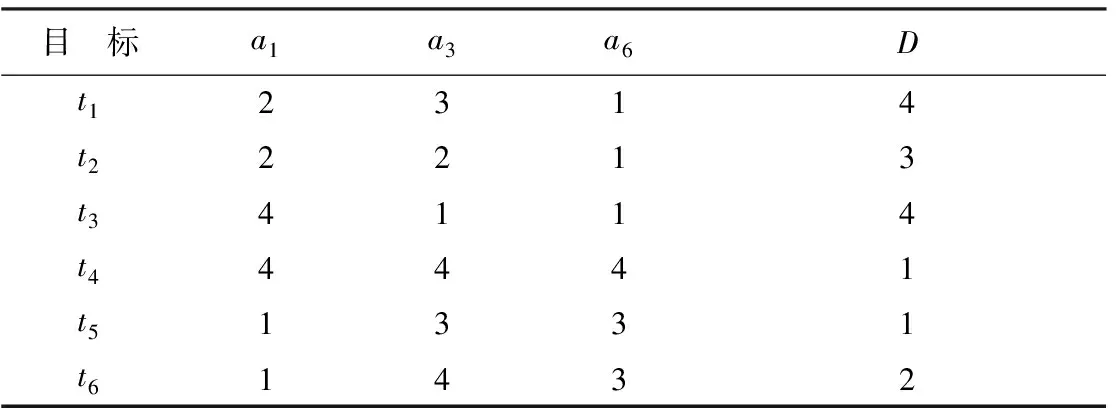
表7 约简后的决策系统

表8 各属性指标下的决策属性权重值
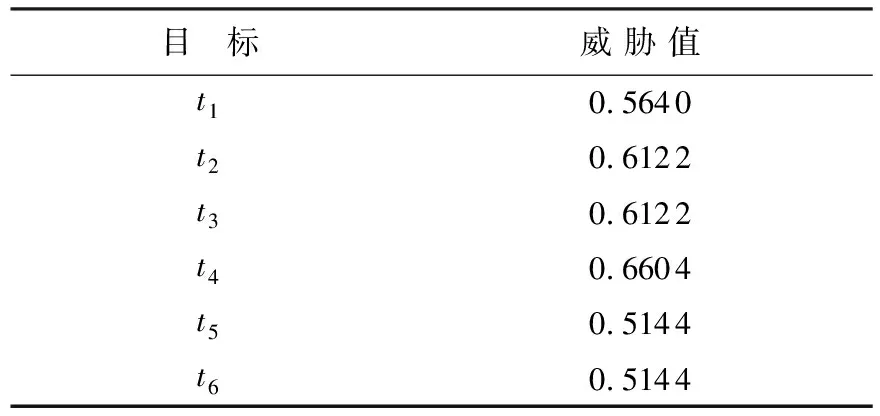
表9 各目标威胁值

图2 仿真决策与样本决策对比Fig.2 Comparison between simulation decision and original decision
5 结 论
1) 采用信息熵方法计算目标属性权重,选取权重最大的属性替代决策属性,构建完备的粗糙集威胁评估模型,实现对空中多目标的定量评估,拓宽了粗糙集理论的适用范围,解决在决策未知情况下的空中目标威胁评估问题。
2) 粗糙集理论在数据支持的基础上,可以减少人为主观因素的影响,且离散化过程对数据具有一定程度的容错性,易于实现实时精确评估,为地面防空系统进行空中目标威胁评估、合理配置防空资源提供了一种新的工程决策方法。
