速解三角函数不等式——单位圆法

靳文岚

（天祝藏族自治县第二中学，甘肃 武威）

一、知识储备

1.任意角三角函数的定义

利用单位圆定义任意角的三角函数.如图1设α是一个任意角，它的终边与单位圆交于点P（x，y），那么：

2.三角函数线

如图1设任意角α的顶点在原点O，始边与x轴非负半轴重合，终边与单位圆相交于点P（x，y），过 P作 x轴的垂线，垂足为 M；过点 A（1，0）作单位圆的切线，它与角α的终边或其反向延长线交于点T.于是有sinα=MP，cosα=OM，tanα=AT

图1

我们把这三条与单位圆有关的有向线段MP，OM，AT分别叫做角α的正弦线、余弦线、正切线。

二、解题原理——利用三角函数线解三角不等式

解：根据任意角三角函数的定义和三角函数线知识，sinα=y=MP，如图2作直线交单位圆于P，Q 两点，要或MP＞满足条件的角α的终边落在图中射线OP，OQ分单位圆所成的上方弧所对扇形区域部分。

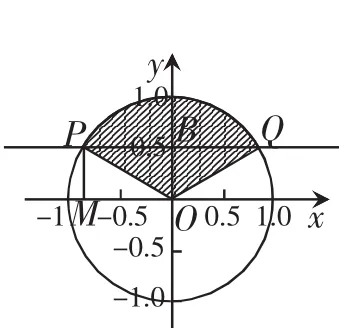
图2

根据上述解法，若要解此类题型，需要求出终边落在射线OP，OQ上角的集合，以及分析出所求区域为射线OP，OQ分单位圆所成的哪一部分便可，由此我们可以得到更简洁快速的方法。

三、快速解三角函数不等式——单位圆法

例1.求满足下列条件的α的取值范围.

图3

图5

四、方法总结

满足条件α的角的终边落在被射线OP，OQ分单位圆所在区域为以下4种情况，其中a∈（-1，1），b∈R

sinα＞a，上方弧所对扇形；sinα＜a，下方弧所对扇形。

cosα＞a，右方弧所对扇形；cosα＜a，左方弧所对扇形。

tanα＞b，一四象限上方弧所对扇形及其对项角所在扇形。

tanα＜b，一四象限下方弧所对扇形及其对项角所在扇形。