电动汽车用双三相永磁同步电机建模及仿真

林 立，彭正苗，万炳呈，石书琪，陈红专，陈鸿蔚

(1.邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000；(2.湖南耐为电控技术有限公司，湖南 长沙，410000；(3.邵阳市电机厂有限公司，湖南 邵阳，422000；(4.湘潭电机集团有限公司，湖南 湘潭，411100)

双三相永磁同步电机具有转矩脉动小、低压大功率、容错能力强等突出优点，在全电飞机、舰船电力推进、电动汽车、风力发电等领域具有广泛的应用前景，因此成为目前的研究热点，备受广大学者的青睐[1-10]。文章应用双d-q变换方法与矢量空间解耦变换方法建立双三相永磁同步电机数学模型，并进行了仿真建模，对其应用于电动汽车上实现高性能控制具有重要意义。

1 双三相永磁同步电机数学模型

相移30°双三相永磁同步电机结构如图1所示，具有A、B、C，X、Y、Z两套Y型三相定子绕组，两套绕组相距30°电角度。uA、uB、uC、uX、uY、uZ、iA、iB、iC、iX、iY、iZ分别为ABCXYZ六相定子相电压、定子相电流，ωe为电角速度。双三相永磁同步电机具有单三相和双三相叠加两种供电模式，其中单三相供电模式与传统三相永磁同步电机一致。在双三相供电模式下，电机的两套空间相差30°电角度的三相绕组分别供给对应时间相差30°的三相交流电源[6-11]。

图1 双三相永磁同步电机结构图Fig.1 A schematic diagram of the geometry of a dual three-phase permanent magnet synchronous motor

1.1 自然坐标系下数学模型

为简化双三相永磁同步电机的数学模型，假设：1)气隙磁场正弦分布；2)忽略铁芯磁饱和效应、集肤效应以及涡流和磁滞损耗；3)忽略绕组间互漏感；4)转子上没有阻尼绕组。

根据图1与电机及电磁理论可得双三相永磁同步电机自然坐标下的数学模型为：

电压方程：

(1)

磁链方程：

ψs=Lsis+γsψfd

(2)

式中：

us=[uAuBuCuXuYuZ]T

is=[iAiBiCiXiYiZ]T

ψs=[ψAψBψCψXψYψZ]T

Rs=diag[RsRsRsRsRsRs]

γs=[sinθsin(θ-2π/3) sin(θ+2π/3) sin(θ-π/6) sin(θ-5π/6) sin(θ+π/2)]T

其中：us为定子相电压矢量；is为定子相电流矢量；ψs为定子磁链矢量；Rs为电阻系数矩阵；Ls为电感系数矩阵；γs为磁链系数矩阵；ψfd为磁链幅值；θ为转子磁极与A相绕组轴线电角度夹角；L11为第一套绕组自感和互感；L22为第二套绕组自感和互感；M12、M21为第一套绕组与第二套绕组之间互感，并且M12=M21。

L11与三相永磁同步电机电感系数矩阵一样，L11为

其中：Laal为漏自感；I3为三阶单位矩阵；Laad、Laaq分别为绕组d轴、q轴主自感。

M12、M21为

L22为

电磁转矩：

(3)

运动方程：

(4)

式中：J为转动惯量；ωm为机械角速度；TL为负载转矩；B为阻尼系数。

从式(1)-(4)可知，双三相永磁同步电机是一个高价、多变量、强耦合的非线性系统，难以实施有效控制。为简化其数学模型，便于控制，分析双d-q变换和矢量空间解耦变换两种简易建模方法。

1.2 双d-q变换数学模型

将双三相永磁同步电机每一套三相绕组看成是一个基本单元，采用传统三相电机建模方法，分别对其进行建模。双d-q坐标变换如图2所示，两套三相绕组clarke变换，分别得到两相静止坐标下数学模型，采用转子磁链定向，对其进行park变换得到两相旋转坐标系下数学模型，其中第一套绕组A相与转子磁链夹角为θ，第二套绕组X相与转子磁链夹角为θ-π/6。

第一套绕组坐标变换

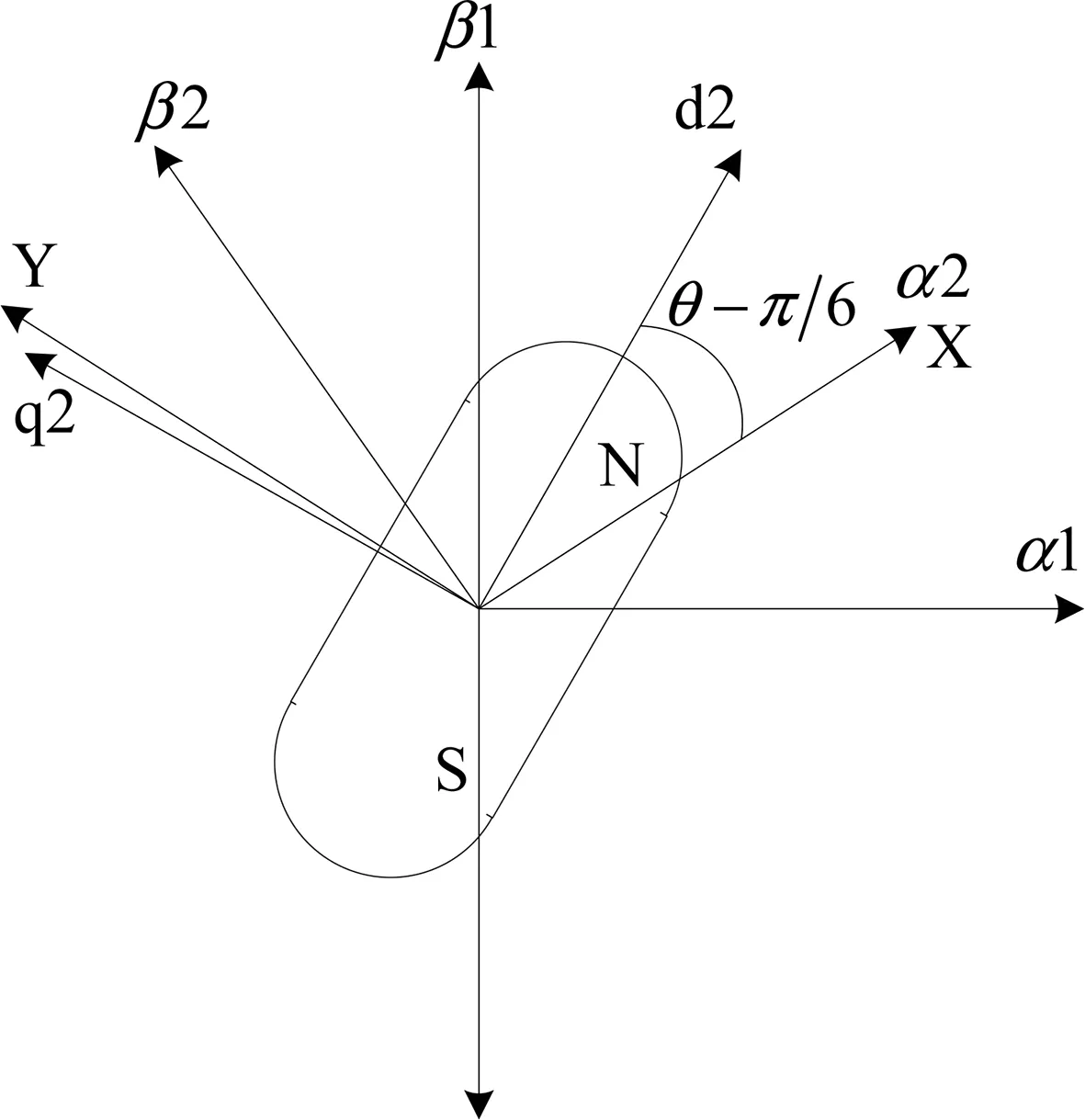
第二套绕组坐标变换

两套绕组clarke坐标变换矩阵Tαβ1，Tαβ2为

(5)

两套绕组park坐标变换矩阵Tdq1，Tdq2为

(6)

(7)

将两套绕组Clarke-Park变换阵组合为

(8)

式中：

将变换阵P代入原始方程中，可以得到每套绕d-q坐标系下的电压和磁链方程。

电压方程：

(9)

磁链方程：

(10)

式中：Ld=1.5Laad+Laal，Lq=1.5Laaq+Laal，Ldd=1.5Laad，Lqq=1.5Laaq。

电磁转矩：

(11)

运动方程：

(12)

将磁链方程(10)代入电压方程(9)中，写成以电流为状态变量的状态方程，即两套绕组在d-q坐标系下电压和电流的关系，表达式为

(13)

式中：

从式(9)-(12)可知，双三相永磁同步电机经双d-q变换矩阵变换后，其数学模型得到简化，从磁链方程可知，两套绕组磁链仍存在耦合。

1.3 矢量空间解耦变换的数学模型

将双三相电机看成一个整体，采用矢量空间解耦坐标变换，可将双三相永磁同步电机各变量映射到α-β、z1-z2、o1-o2三个相互正交平面。坐标变换阵为

(14)

由于机电能量转换只发生在α-β平面中，为了便于电机控制，将α-β平面上各变量进行park变换，得到旋转坐标系下方程，z1-z2、o1-o2平面保持不变，则变化矩阵Tdq为

(15)

总变化矩阵Tr=Tdq·Ts为

(16)

将变换阵Tr代入原始方程中，可以得到α-β平面上d-q坐标系与z1-z2平面上的电压和磁链方程，各变量完全解耦，如图3所示。

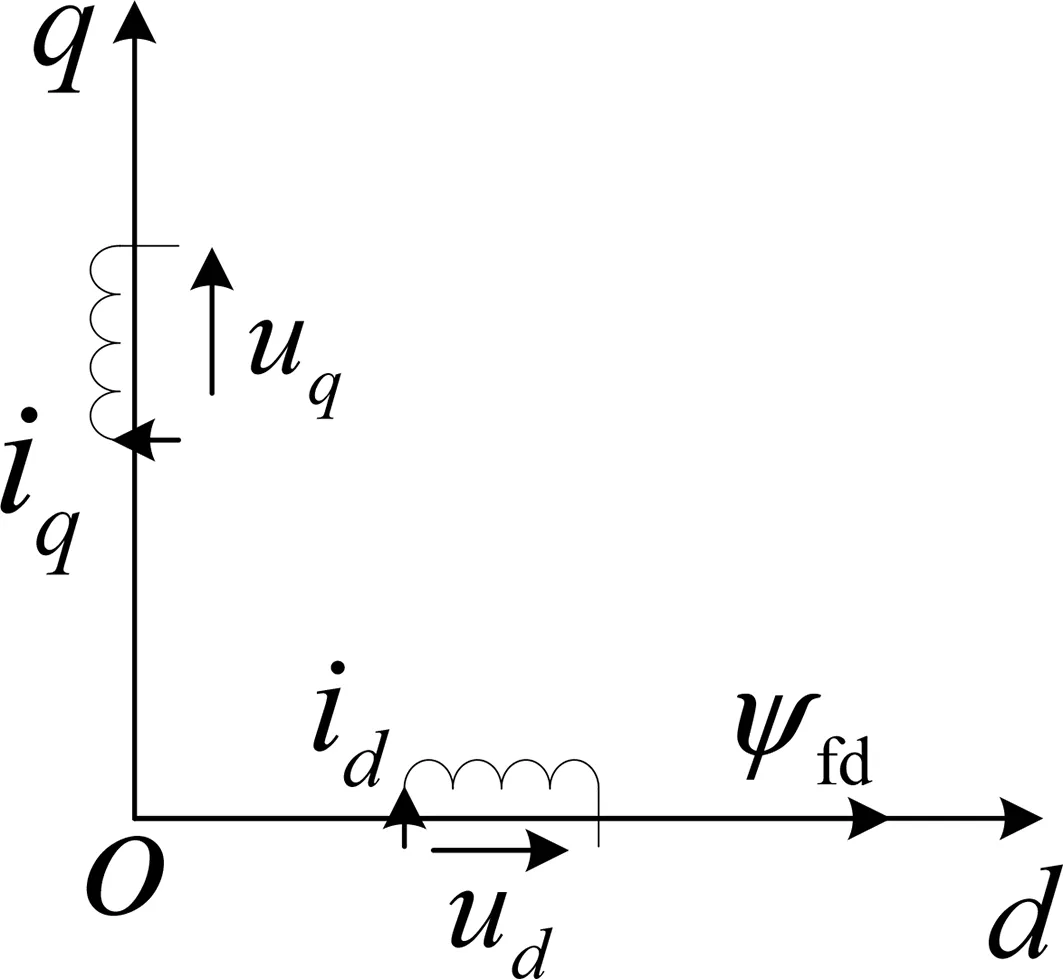
d-q坐标系

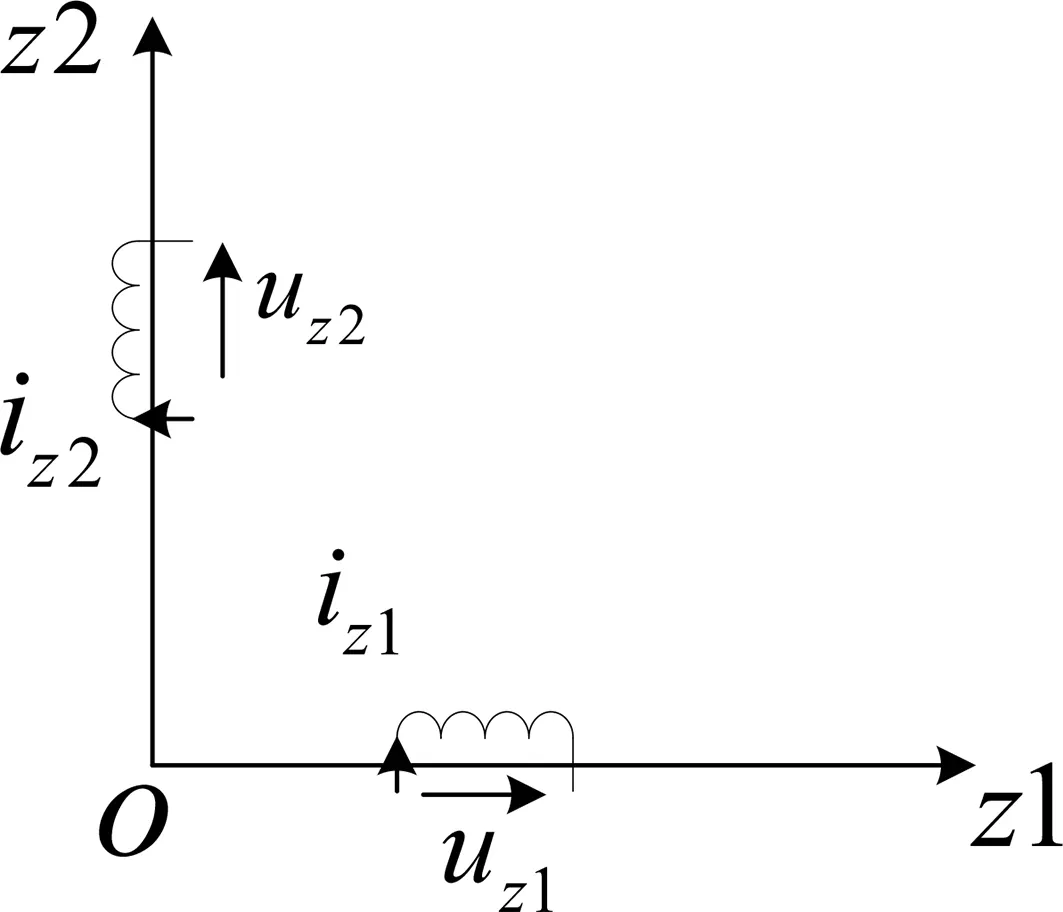
z1-z2平面坐标系

由于o1-o2零序分量平面各变量都为零，因此可以把该平面变量去掉，电压方程为

(17)

磁链方程：

(18)

转矩方程：

Te=3np(iqψd-idψq)

(19)

运动方程：

(20)

式中：LD=3Laad+Laal；LQ=3Laaq+Laal；Lz=Laal。

从方程(17)-(20)可知，矢量空间解耦变换建模使双三相永磁同步电机数学模型得到简化，实现磁链完全解耦，并且把电机中6k±1(k=1,3,5…)次谐波映射到z1-z2平面，便于对谐波的控制，降低电机损耗[17]。

2 双三相永磁同步电机仿真模型

根据双三相永磁同步电机双d-q变换数学模型式(9)-(11)与空间矢量解耦变换数学模型式(17)-(20)，在Matlab/Simulink环境下建立双三相永磁同步电机两种仿真模型，如图4和图5所示。

图4 双d-q变换仿真模型Fig.4 A simulation model of dual d-q transformation

图5 矢量空间解耦变换仿真模型Fig.5 A simulation model of vector space decoupling transformation

电机仿真参数为：np=3；Rs=1.4Ω；Laad=Laaq=1.6mH；Laal=2.4mH；ψfd=0.68Wb；转动惯量J=0.015kg·m2；阻尼系数为：B=0.008。负载转矩TL=50N·m，电压幅值为311V，频率为50Hz，在两种仿真模型上分别给双三相电源信号，仿真结果如图6和图7所示。从图6和图7中可以看出电机稳定运行时电磁转矩为50N·m、转速为1000r/min，分别与给定的负载转矩和相应频率对应的转速一致，模型建立是正确的。两种仿真模型得到的电流、转矩、速度响应曲线一致，可知确定两种模型是等价的。

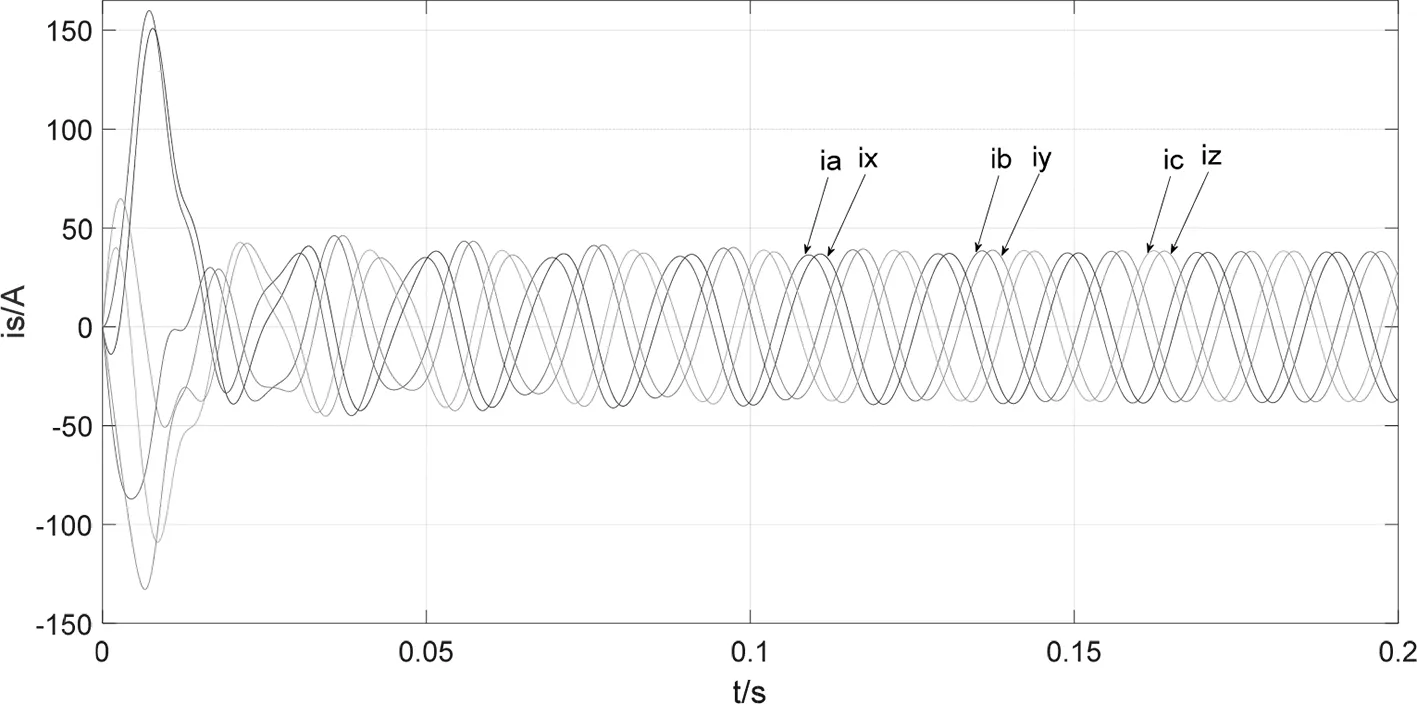
(a)相电流

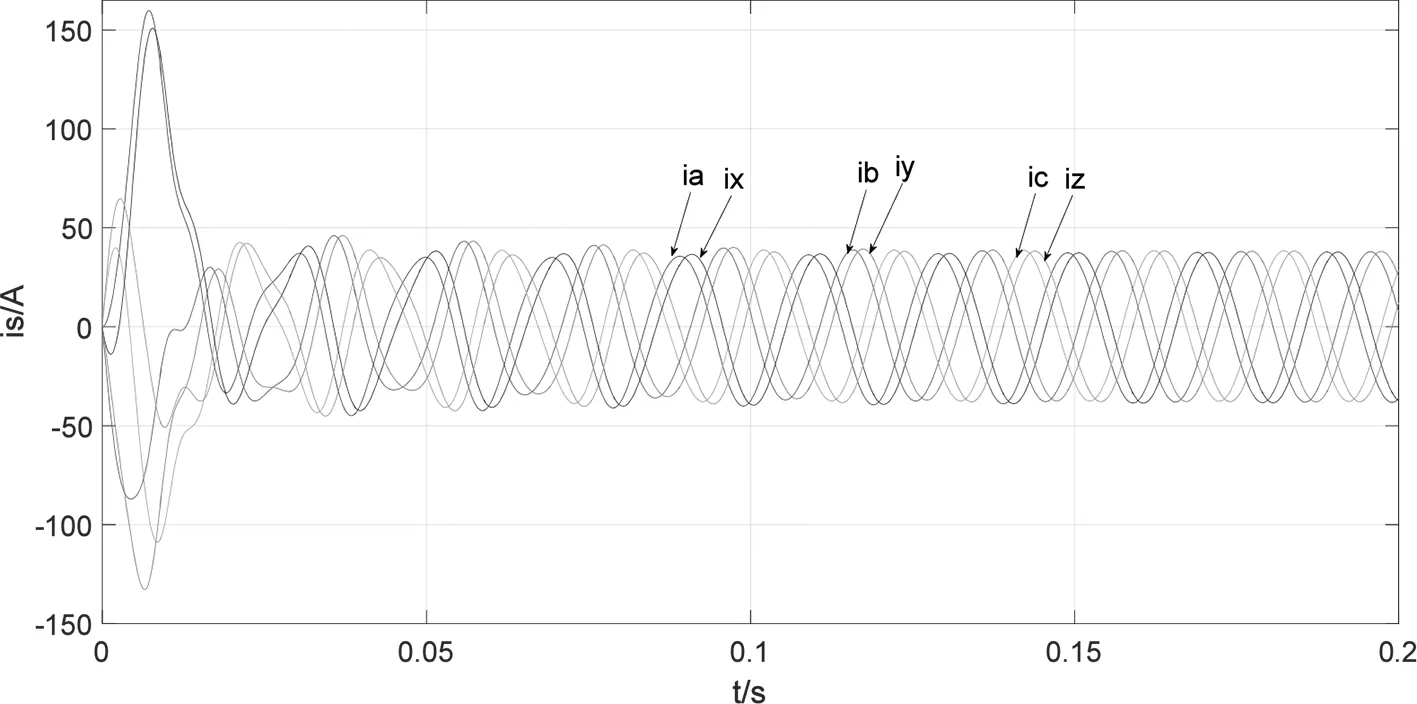
(a)相电流

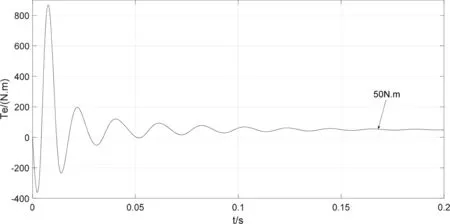
(b)转矩

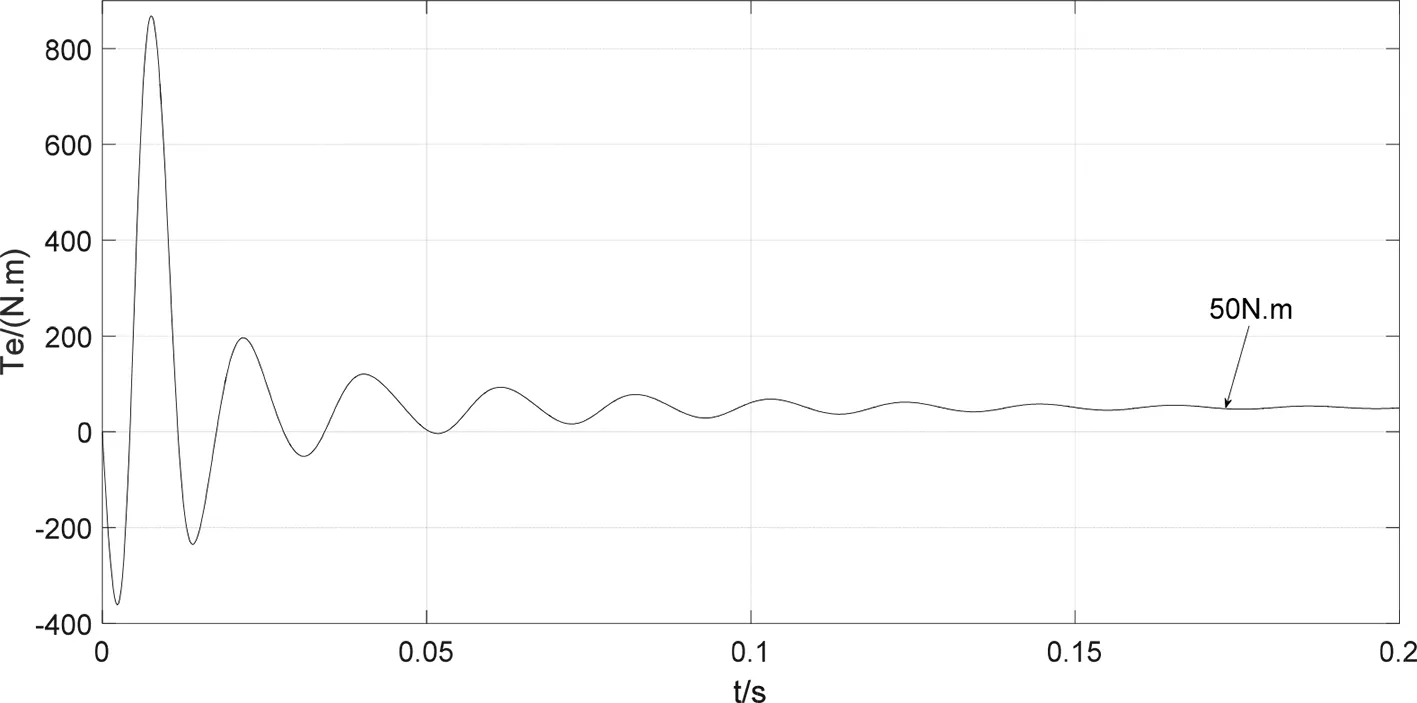
(b)转矩

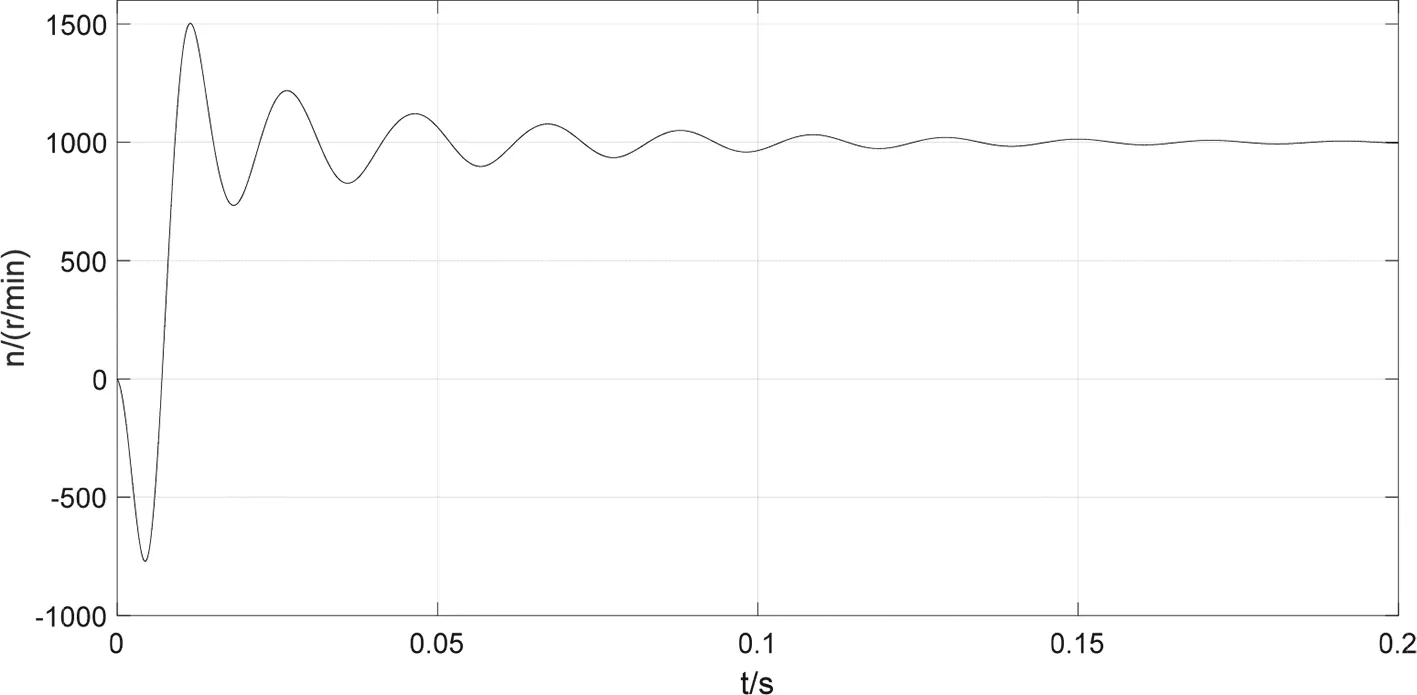
(c)转速图6 双d-q变换模型响应曲线图Fig.6 Response curve of a dual d-q transform model

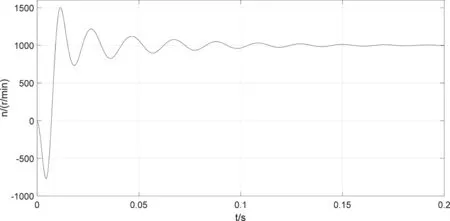
(c)转速图7 矢量空间解耦变换模型响应曲线图Fig.7 Response curve of a vector space decoupling transformation model

3 总结

文中阐述了双三相永磁同步电机自然坐标系下的数学模型与双d-q坐标变换、矢量空间解耦变换两种旋转坐标系下的数学模型，并在Matlab/Simulink环境中搭建了基于双d-q坐标变换与矢量空间解耦变换的仿真模型，仿真结果验证了所建模型的正确性。并且两种模型的电流、转矩、速度响应曲线一致，从而可确定两种模型是等价的，为研究安全、可靠、舒适的电动汽车高性能控制奠定了基础。