联合多源重力数据反演菲律宾海域海底地形
2018-10-26李姗姗孟书宇邢志斌冯进凯
范 雕,李姗姗,孟书宇,邢志斌,冯进凯,张 驰
1. 信息工程大学,河南 郑州 450001; 2. 西安航天天绘数据技术有限公司,陕西 西安 710054
海底地形是全球地形的重要组成部分,海底的地貌形态很大程度上反映了潜在的地质作用,同时海啸波和海洋环流的研究也受限于海深模型的精度。因此,对大地测量、大地构造、海洋地质学和地球物理学等地球科学的研究,离不开对海底地形的深入认识。然而,相较于陆地地形,大多数深海海域还属于未勘探状态,人们对于海洋的认识还很贫乏。传统海底地形数据的获取是通过声呐回波技术进行测量记录,但是对于浩瀚的大洋,通过船舶为载体进行海底地形的绘制不仅耗时耗力,而且船测点分布很不均匀。文献[1]认为依据现有的技术手段完成全球的海底地形测绘任务大概需要花费100~200年时间。1970年以来,Seasat卫星[2]、Geosat卫星[3]、ERS-1[4]和ERS-2[5]卫星,以及T/P卫星[6]等测高卫星提供了高密度、覆盖全球的海面高数据,使得在全球范围内反演海底地形成为可能[7]。
国内外学者对依据重力数据恢复海底地形的方法进行了广泛的研究[8-10]。20世纪70年代,文献[11]详细推导了引力位在频率域的表达式,提出了由于物质界面起伏引起重力异常变化的频率域模型;文献[12]采用交叉谱技术分析了夏威夷皇帝海山链重力异常和海深剖面的关系,研究了考虑地壳均衡的重力异常导纳函数;文献[13]利用测高重力异常、船测海深、ETOPO5模型和GMT海岸线数据,采用卡尔曼滤波技术融合向下延拓方法和线性回归方法推测了南中国海海底地形;文献[14]利用高精度船测重力异常和已知海深模型的先验信息,采用空域法和Parker公式在希腊加夫多斯西南地中海和中太平洋山脊进行了海深预测试验;文献[15]使用ERS-1测高卫星获得的重力数据,融合测深数据预测了西南极洲阿蒙森海(Amundsen Sea)海底地形,试验海域均方根误差结果在120 m以内,并得出了在船测点稀疏海域加入重力数据进行海深反演能提高预测海深结果精度等有益结论。文献[16—17]开展了在考虑地壳均衡补偿效应影响的基础上,依据重力异常采用FFT技术反演海深的研究;文献[18]研究比较了海底地形反演的空域法、频域法和最小二乘配置方法,探讨了海底地形起伏与重力异常垂直梯度之间的响应函数关系,以及高次项和地壳均衡对海底地形反演结果的影响量级;文献[19—20]研究了利用重力异常或者重力异常垂直梯度采用导纳理论反演海底地形的方法。
依据导纳函数构建海底地形模型的过程中涉及诸多地球物理参数的确定。然而,国内大多数文献依赖于经验或者借鉴其他文献信息确定所需的地球物理参数,导致结果与实际海域地球物理情况有所偏差。另外,对于融合重力异常和重力异常垂直梯度推估海底地形,国内学者主要处理方法为利用重力异常和重力异常垂直梯度分别反演不同波段海深,然后将各波段反演海深求和获得最终的海深模型。如文献[21]联合重力异常和重力异常垂直梯度数据反演中国海及其周边海域海底地形时,对于20~100 km波段的海底地形完全采用重力异常反演,100~200 km波段海深仅利用重力异常垂直梯度推估得到。然而,重力异常和重力异常垂直梯度与海深的相关性分析表明,同一波段的海深与重力异常和重力异常垂直梯度均表现出良好的相关性,不仅仅受单一的重力数据影响。
基于以上分析,本文首先根据全球地壳模型CRUST1.0获得研究海域的海水密度、地壳密度、地幔密度以及地壳厚度等地球物理参数,同时,分析重力-海深的“理论导纳”模型和实测数据的“观测导纳”函数,获得研究海域有效弹性厚度的理论计算值。然后,在顾及地壳挠曲均衡影响的情况下,同时考虑不同重力数据对同一波段海深的影响,采用导纳理论联合船测海深数据、重力异常数据和重力异常垂直梯度数据,应用自适应赋权技术分别赋予不同重力数据获得的海深值不同权值,建立菲律宾相关海域的海底地形模型,并利用实际测深数据作为外部检核条件,从检核点差值的角度与国际上通用的V18.1海深模型、ETOPO1海深模型和DTU10海深模型进行精度评价和分析。
1 原理与方法
1.1 导纳理论
重力导纳函数表征将海底地形转换为重力异常的能力[22]。海底是海洋中最浅的密度界面。海洋深度变化可以认为是质量单元的高度变化。海洋深度变化将会影响重力场发生相应变化,如图1所示。扰动位的变化为
(1)
式中,G为地球引力常数,通常取6.673×10-8cm3/g·s2;Δρ为地壳与海水的密度差异;r是研究点p的地心向径;r-r′为单元质量(流动体元)dm的向径;dv为积分体元。

图1 质量亏损与重力异常关系Fig.1 The relationship between mass loss and gravity anomaly
根据布隆斯公式,可由式(1)得到大地水准面高并转化为球体表面的离散质量单元计算扰动引力。那么大地水准面高的离散化形式为
(2)
式中,γ为正常重力;ΔΩ(r′)为球体质量单元的球面面积;Zb、Zt分别为质量单元的底部和顶部高度。单元质量高度为Z(r′),计算公式为Z(r′)=Zt-Zb。将其转换到频率域上进行处理,得到
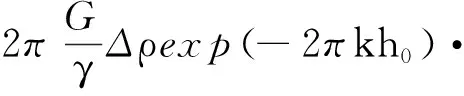
(3)
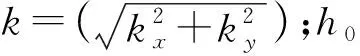
当海底地形出现特殊的海底地貌时,如海山、海底高原等,需要考虑均衡的影响。那么由式(3)可以得到顾及均衡效应时,使用重力异常Δg(r′)反演海底地形的补偿海深,如式(4)所示
(4)
式中
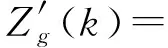
(5)
式中,Tc为平均地壳厚度;Δρ′为地幔与地壳的密度差异;D为岩石圈挠曲刚度;岩石圈刚度D与有效弹性厚度Te关系为[6]
(6)
式中,E为弹性模量;v为泊松比。
由重力异常垂直梯度与重力异常之间的导数关系,依据傅里叶变换求导法则,对式(4)求导得到顾及挠曲补偿情况下,重力异常垂直梯度的导纳函数为
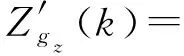
(7)
1.2 有效弹性厚度
导纳理论反演海底地形时涉及有效弹性厚度的获取。有效弹性厚度定义为:在地质时间尺度上(一般大于106年),如果覆盖在软弱流体层(软流圈)上的岩石圈对负载(如岩石圈上负载和下负载,地形等)所作出的响应,和薄性弹性板类似,那么薄性弹性板的特征厚度即所谓的岩石圈有效弹性厚度[23]。由此可见,有效弹性厚度不可观测,为板块理论中的理论值。
20世纪80年代,文献[24]提出了采用海底地形数据和重力异常数据在频率域内计算实测海底地形和重力异常“观测导纳”的理论公式,如式(8)所示
G(k)=Z(k)H(k)+Ng(k)
(8)
式中,G(k)和H(k)分别为重力异常g和海底地形h的傅里叶变换;Ng(k)是由于地球内部密度分布不均匀引起的地质噪声;Z(k)为重力异常和海底地形的“观测导纳”,表示单位地形负载和其区域均衡补偿引起的重力脉冲响应[25]。
实际计算过程中,“观测导纳”采用对不同频率k取半径为δk的圆环,然后求取圆环内的全方位平均的方法获得“观测导纳”,由于噪声Ng(k)与海底地形H(k)不相关,那么其统计结果接近于0。最终,“观测导纳”表示为
(9)
式中,〈〉为频率域δk圆环内全方位的平均;Re表示取复数的实部;G*(k)、H*(k)分别表示重力异常和海底地形傅里叶变换的复共轭。
1.3 相关性分析
相关分析源于统计学,具有实用、适用性强和方法简单等优点。对于确定性信号,很多时候使用信号的时域或频率相关进行分析。在地球物理学的研究中,常常使用信号在频率域中的相干性(相关性的频率域表达)对有关地球物理数据进行分析[24,26]。
假设信号分别为x(t)、y(t),那么,信号x(t)、y(t)在频率上的相干性[27]可表示为
(10)
式中,Sxω、Syω分别为信号xt和yt的自功率谱密度函数;Sxyω为xt和yt互谱密度函数。
2 试验结果与分析
2.1 数据准备和前期处理
本文选取菲律宾海4°×4°(17°N—21°N,132°E—136°E)海域范围为研究区域。由于基于导纳函数的海底地形反演方法在频率域上进行,为消除边缘效应的影响,试验过程中选取的研究范围在纵向和横向方向上分别向外延拓1°,然后对反演结果进行截取处理得到研究海域的海底地形。数据来源如下:①卫星测高重力异常数据来自于丹麦科技大学(Technical University of Denmark)空间实验室(DTU Space)发布的1′×1′DTU10模型;②重力异常垂直梯度数据来自SIO,UCSD(Scripps Institution of Oceanography,University of California,San Diego),版本V24.1,2016年2月发布,相较于V23版本,加入了超过12个月的Cryosat-2卫星数据[28];③船测海深数据来源于NGDC(National Geophysical Data Center)发布的研究海域实测数据。首先依据3σ准则对实测数据进行粗差剔除,最终得到15 039个海深测量点,选取其中大约4/5的船测数据作为海域控制点(图2中黑色五角星所示),余下的测量点作为外部检核的检核点(图2中红色三角形所示),图2的背景为ETOPO1海深模型。
根据全球地壳模型CRUST1.0获得研究海域的相关地球物理信息[29]。具体为:海水密度(ρw)为1020 kg/cm3;地幔密度(ρm)为3 329.2 kg/cm3;地壳密度(ρc)为2 816.7 kg/cm3;平均地壳厚度(Tc)为6.880 4 km,同时泊松比(v)和弹性模量(E)参考国内外处理经验分别取为0.25和100 Gpa。
本文依据重力-海深的“理论导纳”和实际数据的“观测导纳”进行比对分析获得有效弹性厚度的数值估计。其中,“理论导纳”和实际数据的“观测导纳”分别依式(5)和式(9)进行计算。有效弹性厚度Te分别取6、10、15和20 km时的“理论导纳”与“观测导纳”(图3中折线)对比如图3所示。
由图3可以看出,低频部分的曲线主要受有效弹性厚度(Te)的影响,反映了深度物质的重力影响;高频部分的曲线走势主要受海深的影响,受有效弹性厚度影响较小,反映了浅部物质的重力影响。从而对于有效弹性厚度的确定,着重研究极值点附近低频部分的导纳函数状态。从图3可以看出,当有效弹性厚度取10 km时,“理论导纳”在低频部分与“观测导纳”最为接近。基于以上分析,最终得到研究海域的有效弹性厚度为10 km。
根据式(10)对重力异常和重力异常垂直梯度与海深进行相干性分析,得到不同波段的相干性结果如图4所示。其中,黑色圆点和蓝色圆点分别表示重力异常与海深的相干性,以及重力异常垂直梯度与海深的相干性结果。
从图4可以看出,波长范围为60~140 km时,重力异常和重力异常垂直梯度与海深的相关性均在0.5以上。因此,本文选择在该波段内利用重力数据进行海底地形反演。
2.2 海深模型反演
由以上分析可知,海底地形与重力数据在60~140 km范围内呈现出较强相关性,本文拟采用移去恢复技术构建海深模型,步骤如下:
(1) 将海域控制点进行格网化处理得到格网化海深。
(2) 格网化海深进行傅里叶变换并进行滤波处理,获得相应波段的海深。
(3) 顾及地壳挠曲均衡条件下,采用重力异常和重力异常垂直梯度作为单一重力数据源,分别在60~140 km波段范围内反演出相应波段海深值。
(4) 60~140 km波段范围内,应用自适应赋权技术赋予不同重力数据获得的海深值不同权值。将各个波段得到海深值相加构建最终的海深模型。并将模型值与检核点进行较差比较,获得不同赋权情况下海深模型的均方差。最小均方差对应的权组合为最佳赋权值。
图5为在60~140 km波长范围内,分别赋予重力异常和重力异常垂直梯度反演海深结果不同权值情况下,获得的最终海深模型与检核点比较的均方差结果图。从中可以看出,随着重力异常垂直梯度反演结果与重力异常反演结果的权比增大,海深模型的检核均方差呈现先减小后增大的趋势。当重力异常垂直梯度反演结果与重力异常反演结果的权比为2∶3时,构建的海深模型检核精度最高。当仅采用重力异常和重力异常垂直梯度作为数据源时,海深模型的检核精度分别为140.42 m和172.89 m。
通常情况下,重力异常构建波长小于100 km的海底地形,重力异常垂直梯度构建100~200 km波段的海底地形[21]。本文通过相干性分析后,选择在相干性较强的60~140 km波段范围内进行数据处理。从图5不同权值的检核结果看,当重力异常垂直梯度反演结果与重力异常反演结果的权比为2∶3时,重力异常垂直梯度将会对重力异常的噪声产生抑制作用。
基于以上分析,当重力异常垂直梯度反演结果与重力异常反演结果的权比为2∶3时,联合重力异常和重力异常垂直梯度在60~140 km波长范围内反演海底地形(以下称为本文模型)和仅利用重力异常构建的海深模型(以下称为模型1)与重力异常垂直梯度构建的海深模型(以下称为模型2),结果如图6(a)、图6(b)和图6(c)所示。红色圆点表示模型值与检核点比较差值大于300 m的检核点分布情况。其中,本文模型有83个检核点较差值大于300 m,模型1和模型2分别有177个点和238个点。
从图6可以看出,3种模型在海底地形起伏较小区域反演结果相差不大,但是在地形起伏剧烈的海山附近(研究海域东南方向存在一列线性海山),不同数据源存在不同的反演效果。对比图6(b)和图6(c)差值点分布情况可以看出,模型1在海山链周围的反演精度明显小于模型2;在海山链上,模型2差值大于300 m的检核点明显多于模型1,模型1在海山链上的反演效果优于模型2。联合重力异常和重力异常垂直梯度生成的本文模型(图6(a))差值点大于300 m的个数仅有83个。结合图6(a)和图6(b)可以看出,在海山链周围海域,本文模型反演结果远远优于模型1;对比图6(a)和图6(c),本文模型在海山链上的反演精度又明显好于模型2。通过以上分析可以得出,联合重力异常和重力异常垂直梯度反演海底地形能够综合重力异常和重力异常垂直梯度在对待不同海底地形上的反演优势,生成精度优于单独使用重力异常数据和重力异常垂直梯度数据反演的海底地形模型。
为进一步验证联合重力异常和重力异常垂直梯度在构建海底地形模型方面的优势,将联合重力异常和重力异常垂直梯度构建的海深模型、重力异常和重力异常垂直梯度分别构建的海深模型与检核点进行比较,得到统计结果见表1。
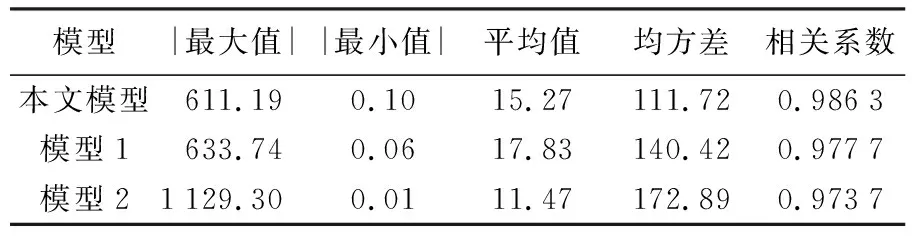
表1 模型检核统计结果
表1统计结果表明,本文模型、模型1和模型2与检核点的较差均方差分别为111.72、140.42和172.89 m。相比于模型1和模型2,联合重力数据反演海深精度分别提高了20.43%和35.38%左右。从而进一步验证了联合重力异常和重力异常垂直梯度反演海底地形模型优于利用单一重力数据反演结果。
2.3 精度评价
利用反演海深模型值内插到检核点进行外部检核比较,同时计算插值点与检核点的相关系数,并选用国际上通用的V18.1海深模型、ETOPO1海深模型和DTU10海深模型进行联合对比分析,对本文模型精度进行验证和评估。各模型检核比较结果见表2。

表2 各模型检核统计结果
由表2统计结果可以看出,本文模型与检核点比较的差值最大值为611.19 m,均方差为111.72 m,V18.1海深模型、ETOPO1海深模型和DTU10海深模型检核较差最大值分别为500.85、1 070.60和1 785.90 m,均方差分别为96.18、153.40和183.22 m。在研究海域,本文模型精度总体上优于ETOPO1模型和DTU10模型;本文模型与V18.1模型相比,检核差值的最大值、最小值和平均值相差不大,而检核差值均方差略低于V18.1模型。究其原因,笔者认为可能是两种海深模型建立过程中使用的源数据、数据预处理流程与方法以及船测数据质量等方面的差异导致。相较于ETOPO1海深模型和DTU10海深模型,本文联合重力异常和重力异常垂直梯度反演海深模型精度分别提高了27.17%和39.02%。本文模型、V18.1海深模型、ETOPO1海深模型以及DTU10海深模型与检核点比较的相关系数分别为0.986 3、0.989 3、0.972 4和0.959 7,相关系数统计结果与模型的差值统计结果相一致,本文模型与V18.1海深模型相比较相关系数仅差0.3%左右,但是本文模型依然优于ETOPO1海深模型和DTU10海深模型。
进一步比较4种海深模型在研究海域的精度信息,定义模型海深与检核点的差值与检核点海深之比为相对误差。4种模型的相对误差统计结果见表3。

表3 各模型相对误差统计结果
相对误差统计结果显示,本文模型无论在相对误差的最大值、最小值和平均值方面均明显小于ETOPO1模型和DTU10模型,与V18.1海深模型的统计结果较为接近。同时,本文模型、V18.1模型、ETOPO1模型和DTU10模型的相对误差标准差分别为2.45%、1.95%、3.58%和3.89%。相较于ETOPO1模型和DTU10模型,本文模型相对误差精度分别提高31%和37%左右。统计本文反演海深模型的相对误差频率分布和空间分布分别如图7和图8所示。
图7显示本文反演海底地形模型相对误差绝对值在2.5%范围内占79.30%左右,相对误差绝对值在5%范围内大约占94.25%。结合图8相对误差的空间分布情况,在绝大部分海域,本文反演模型相对误差较小,模型反演海深精度较高。若将检核点相对误差大于7%的海域定义为反演精度较低区域,图9中红色圆点为反演精度较低的检核点分布情况。
图9显示红色圆点大多数集中在海山区域,这些海域由于海山的存在,往往地形起伏剧烈。而在其他海域零星的几个低精度检核点则可能是在数据预处理粗差剔除阶段,船测粗差未及时发现所导致。若存在测量粗差的船测数据隐藏在控制点中,将影响最终模型精度;若检核点中存在粗差的船测数据,则会对之后的模型精度评价产生误导和干扰。总之,依据图9低精度检核点的空间分布情况,说明地形剧烈起伏对海深模型精度影响较大,这与国内外研究结果相符合。
针对以上情况,可以考虑不同数据反演不同海底地形方面的优势进行联合反演,以期达到理想效果。
3 总 结
本文选取菲律宾相关海域4°×4°(17°N—21°N,132°E—136°E)范围为研究区域,同时考虑研究海域均衡挠曲影响,依据CRUST1.0模型和相关板块理论获得了研究海域有关的地球物理参数,联合重力异常和重力异常垂直梯度数据,并应用自适应赋权技术分别赋予不同重力数据获得的海深值不同权值,采用导纳函数方法开展了海底地形反演试验。反演结果与目前国际上通用的V18.1海深模型、ETOPO1海深模型和DTU10海深模型进行了外部检核比较分析,得到如下有益结论:
(1) 依据重力-海深的“理论导纳”和实际数据的“观测导纳”进行对比分析发现,导纳函数曲线在极值点附近低频部分主要受有效弹性厚度影响。分析表明有效弹性厚度为10 km时,研究海域的“理论导纳”和“观测导纳”最为接近。
(2) 联合重力异常和重力异常垂直梯度反演海底地形能够综合重力异常和重力异常垂直梯度在对待不同海底地形上的反演优势,生成精度优于仅利用单一重力数据的反演海深模型。相较于仅利用重力异常构建的海深模型(模型1)和重力异常垂直梯度构建的海深模型(模型2),联合重力数据反演海深精度分别提高了20.43%和35.38%左右。
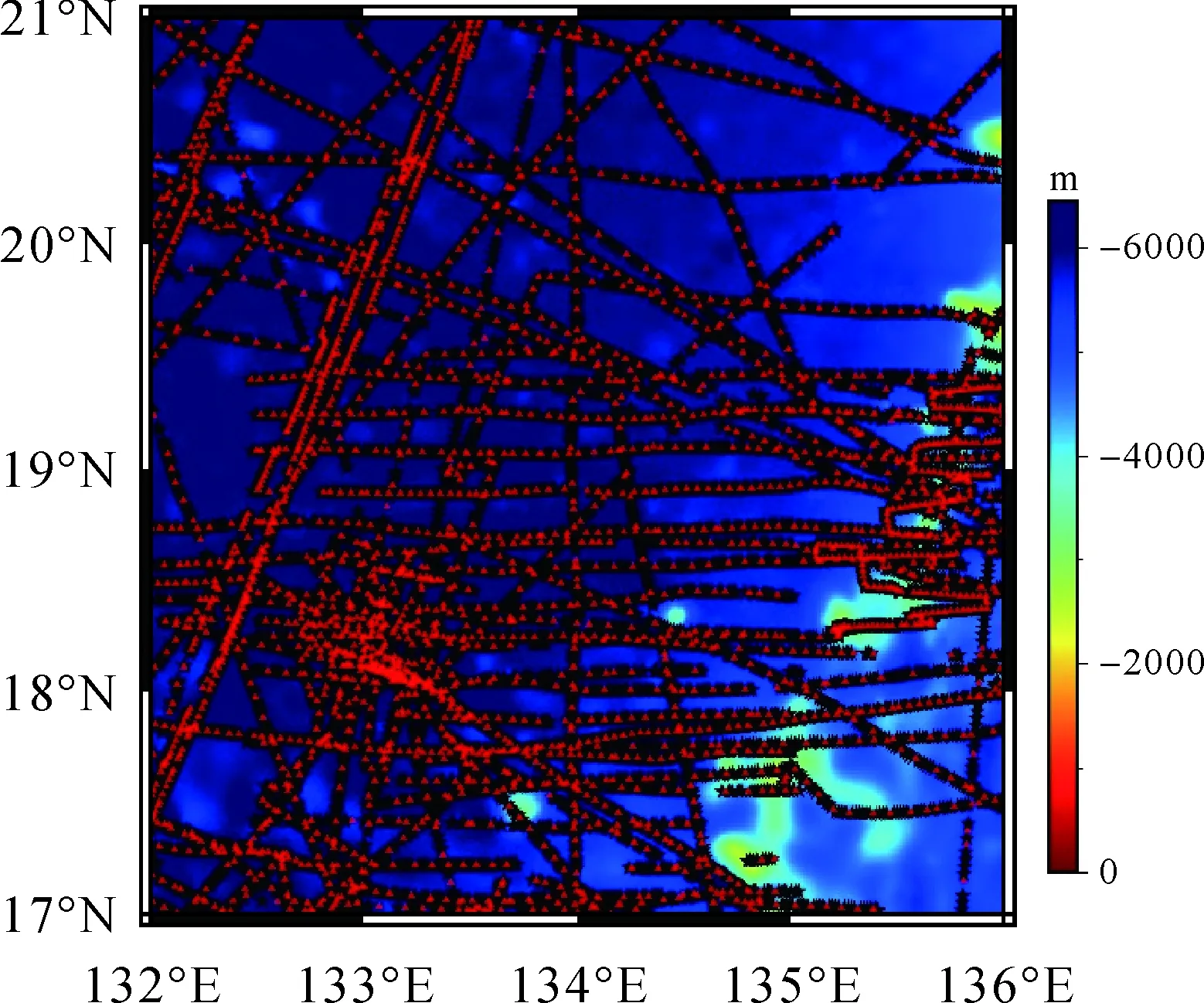
图2 船测点分布Fig.2 Ship survey point distribution
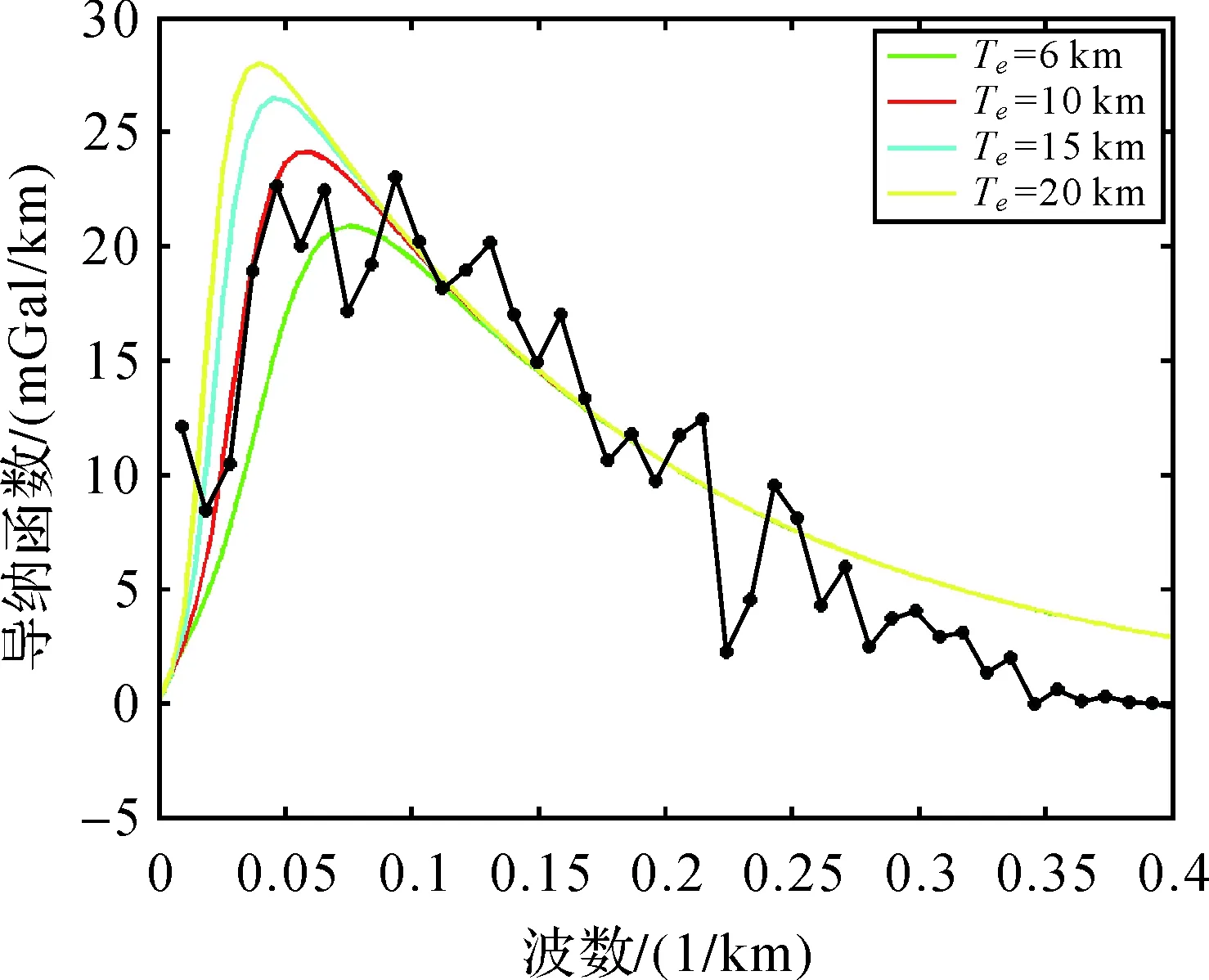
图3 导纳函数Fig.3 Admittance function

图4 重力数据与海深的相干性Fig.4 Coherence between gravity data and sea depth

图5 不同权值下的检核结果Fig.5 The accuracy of the results under different weights

图6 反演海深模型Fig.6 Inversion sea depth model
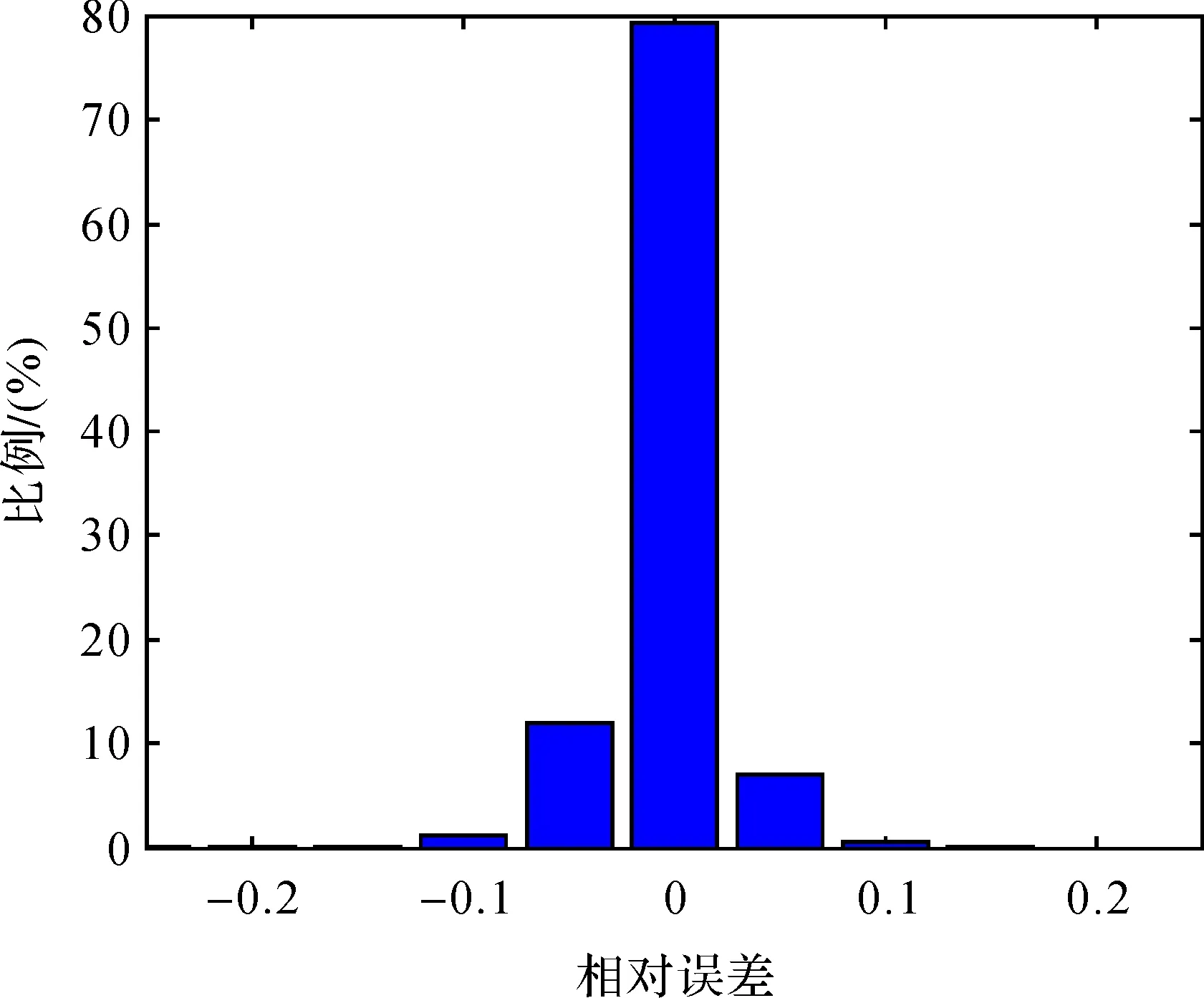
图7 反演模型相对误差Fig.7 Inverse model relative error
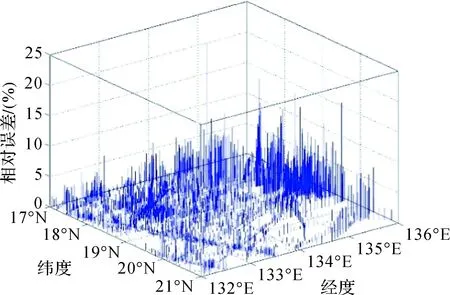
图8 反演模型相对误差分布Fig.8 Inverse model relative error distribution

图9 低精度检核点空间分布Fig.9 Spatial distribution of low precision points
(3) 根据船测数据进行外部检核发现,研究海域范围内,本文反演结果的模型精度略低于V18.1海深模型,优于ETOPO1海深模型和DTU10海深模型。相较于ETOPO1海深模型和DTU10海深模型,本文反演结果精度分别提高了27.17%和39.02%左右。
(4) 研究海域范围内,4种海深模型值(本文模型、V18.1模型、ETOPO1模型和DTU10模型)与检核点的相关系数和相对误差比较结果显示,本文反演模型与V18.1模型较为接近,优于ETOPO1模型和DTU10模型。反演海深模型精度较低部分主要集中在海底地形起伏剧烈的多海山区域。绝大部分海域反演海深相对误差绝对值在5%范围内。
