稳健估计的一种改进迭代算法
2018-10-26黄李雄曾文宪
方 兴,黄李雄,曾文宪,吴 云
武汉大学测绘学院,湖北 武汉 430079
当观测值不含粗差、观测误差服从零均值的分布时,经典最小二乘估计具有最优无偏性。然而,在实际的数据采集中经常会出现粗差,由于最小二乘不具有抗差性,对粗差观测值十分敏感,少量的粗差就可能对最小二乘估计结果产生破坏性影响[1-6]。因此,在粗差干扰出现的情况下,选择适当的估计方法,尽量降低或者去除粗差对参数估值的影响,得出正常模式下的最优或接近最优的参数估值,即为测量数据处理领域稳健估计的基本思想。对于现代空间测量技术如GNSS、摄影测量与遥感等,利用稳健估计处理自动化采集、海量的测量数据中混入的粗差具有重要的理论和实际意义。
1953年,文献[7]首次提出了稳健估计(又称为抗差估计)这一专业术语。文献[8]提出了污染分布模式。文献[9]阐述了定位参数的抗差估计。文献[10]提出了影响函数和崩溃点的概念。这些都为稳健估计理论奠定了基础。1980年,文献[11]将稳健估计理论引入测量界,提出了著名的“丹麦法”。此外,国内学者在稳健估计方面也取得重大突破,如文献[12]提出等价权的概念;文献[13]提出自适应的稳健估计算法等。目前,稳健估计可以分为3大类:M估计、L估计、R估计。其中,M估计是经典极大似然估计的推广,是测量数据处理中稳健估计最重要的估计方法。
稳健估计的选权迭代算法属于M估计,在测量中应用广泛。基本原理为:首先采用最小二乘法得到观测值的估计残差;根据残差确定各观测值新的权因子,进行下一轮平差计算;反复迭代,直至前后两次估计值的变化值小于限差为止。算法每次迭代求解法方程均需进行矩阵的求逆运算,矩阵求逆的复杂度是其维数的三次方。因此,平差模型的待估参数多,即法方程正交矩阵维数高,算法的计算量和计算时间急剧上升,算法效率难以满足现代测量中大规模测量方案、海量数据及平差模型实时解算等要求。
本文基于矩阵逆的运算法则,提出了一种有效改进现有选权迭代算法的方法。迭代计算中,仅需计算由前一次残差确定的新权阵下的模型未知参数估计值的变化量,避免了法方程正交矩阵的求逆,显著提高了算法的效率,并能保持原稳健权函数的抗差性。本文以水准网为例,通过增加估计参数的数量和粗差数量,验证了当模型的估计量增加时,改进的选权迭代算法的计算效率要远高于经典选权迭代算法。
1 经典选权迭代算法
设平差的线性函数模型和随机模型为
(1)
式中,l为观测值向量;B为系数矩阵并且列满秩;x为未知参数向量;Δ为误差向量;D为对角方差-协方差矩阵;σ0为单位权中误差;Q为对角协因数矩阵;P为对角权阵。
独立不等权观测情况下的M估计准则为
(2)


(3)
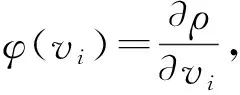
(4)

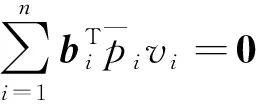
(5)

将式(3)代入式(5),得到M估计下的法方程
(6)
解式(6)得
(7)
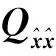
根据残差v确定各观测值新的权因子,再进行下一轮平差,反复迭代直至前后两次估计值的变化小于限差,计算结束。算法的核心是确定权函数ρ(或φ),即由每次迭代的残差估计值确定新的权阵,以保证估值的抗差性和效率[13]。以下介绍几种常见的权函数。
(1) Huber法[14-17]
(2) Danish法[18-20]
(3) IGGⅢ方案[21-23]
c1=1.5,c2=3.0
以上权函数中,w(u)为权函数,c1和c2为相应的调和系数。
2 改进选权迭代算法
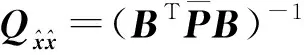
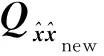
(8)
式中

(9)
将式(9)代入式(8)得
(10)
根据矩阵求逆引理[24-25]
(A+UCV)-1=A-1-A-1U(C-1+VA-1U)-1VA-1
(11)
将式(10)展开
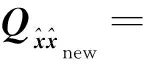
(12)
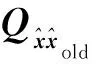
(13)
式(7)中,令wold、wnew分别表示权阵更新前后的权阵,则
wnew=BT(P+dP)l=BTPl+BTdPl=wold+dw
(14)
式中,dw为
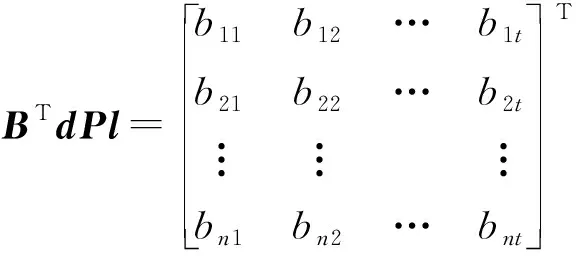
(15)
令
(16)

由式(12)—式(16)得
[wold+bi·dpili]=
diλ-diγ-1β-diγ-1αλ=
[λ(γ-α)-β]γ-1di
(17)

则式(13)可表示为
(18)
改进选权迭代算法步骤总结如下:
(1) 估计最小二乘初值:
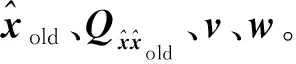
(2) 选权迭代计算:
我的姐姐们整天跟着父亲下地,不是薅草,就是栽苗挖苕,总有干不完的活儿。母亲虽然不允许我走出院子,但她有时候竟忘了我的存在。她喂了更多的鸡和猪,每天要打几背篓的草,还要切细剁碎,哄着那些牲口吃光。我沉闷极了,孤零零地坐在院子边,等着有人经过时和我说上几句话。


3 实例分析
为了从数值上说明改进选权迭代算法在计算效率上的优势,笔者设计了一个条状、结构规整的水准网实例,如图1所示。点A、B、C、D为已知控制点,其余为未知点,未知点个数为t(t为偶数),观测值个数为n,且n=1.5t+2。
水准网设计试验数据数据说明如下:
控制点高程:HA=1 m,HB=0 m,HC=1.5 m,HD=0.5 m
高差观测值:
h1=h2=h7=h8=…=(0.5+Δ)m
h4=h5=h10=h11=…=(-0.5+Δ)m
h3=h6=h9=h12=…=(1+Δ)m
式中,Δ为符合正态分布(μ=0,σ=0.005)的随机
误差,设计粗差的量级约为1 m。
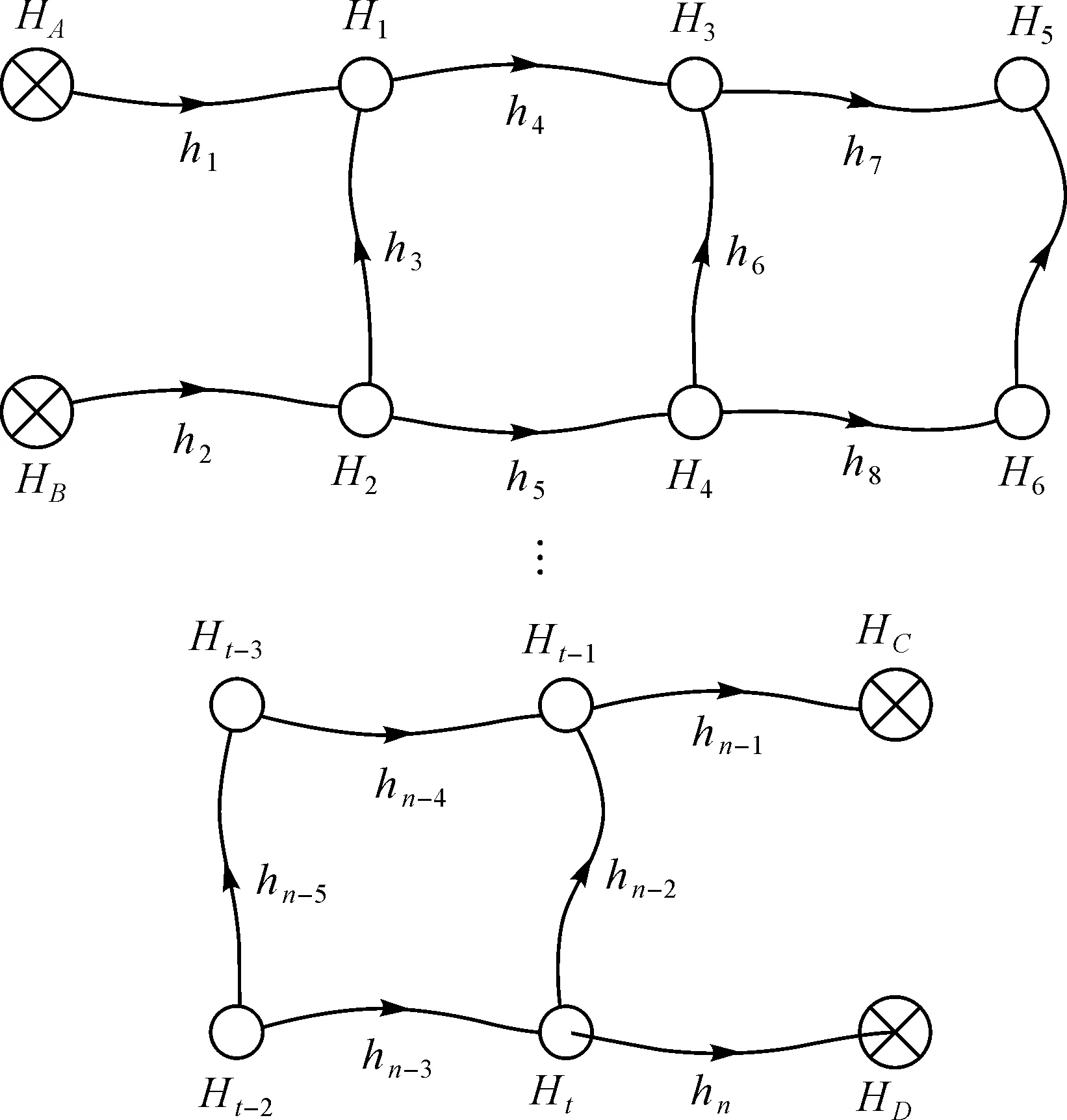
图1 模拟的水准网Fig.1 Simulated leveling network
当水准网包含不同数量级的未知点t=100、500、1000、5000、10 000时,且分别包含1到5个粗差的情况下,笔者采用Matlab编程对改进选权迭代算法与经典算法的计算效率进行了比较。程序采用Matlab自带的tic/toc函数,记录了算法改进前后程序运行所需时间,试验结果见表1。

表1 运行时间对比
试验结果表明:
(1) 改进算法计算效率要高于经典选权迭代算法(图2、图3),尤其是在平差模型中待求参数个数t较大或者多个粗差的情况下,计算效率显著提升。当未知数个数t=10 000且含5个粗差时,改进算法所需计算时间仅为经典算法的1/30。
(2) 改进算法的计算效率取决于采用最小二乘估计初值的计算时间,迭代计算无需求逆,当粗差个数增加时,计算时间仅有微小增长。例如,当未知数个数t=10 000,粗差从1个增长到5个时,经典算法计算时间急剧增长,由829 s增加4倍,达到3285 s;而改进算法从100 s仅增加到109 s,改进算法对于处理多个粗差情况非常高效。
4 结 论
经典选权迭代算法属于M估计,是当前运用最为广泛的稳健估计方法之一。本文采用矩阵逆运算法则,提出了一种改进的选权迭代算法。改进算法在迭代过程中,仅需计算新权阵下的最小二乘估计改正值,避免了经典算法中每步对平差模型法方程的求逆运算,显著提高了算法的计算效率。改进选权迭代算法适用于现代空间测量技术下对自动观测的海量数据的实时或者准实时的处理需求,如GNSS、遥感等观测数据,当这些数据含有一定数量的粗差时,改进算法可以大大降低经典选权迭代算法的计算时间。本文算法基于独立不等精度观测值的情况,笔者下一步的研究目标是针对海量数据,讨论如何提高相关观测值[5,17,26]的选权迭代算法的计算效率。

图2 改进前后运行时间比较(未知点数为10 000)Fig.2 Computational cost comparison when the unknown parameters is 10 000

图3 改进前后运行时间比较(误差数为5)Fig.3 Computational cost comparison when there are 5 errors
