通过大港验潮站坐标确定我国高程基准的垂直偏差
2018-10-26吴富梅魏子卿刘光明
吴富梅,魏子卿,刘光明
1. 地理信息工程国家重点实验室,陕西 西安 710054; 2. 西安测绘研究所,陕西 西安 710054
我国目前采用的1985国家高程基准是由青岛大港验潮站处平均海平面定义的[1-3]。平均海面的重力位是我国高程基准的重要基础数据,也是实现我国高程基准与世界高程基准统一的重要依据[4-7]。
全球高程基准由大地水准面定义,大地水准面是全球范围内平均海面最佳拟合的重力等位面。IERS规定,全球大地水准面重力位W0=62 636 856.0 m2s-2±0.5 m2s-2,是由文献[8—11]利用T/P卫星的全球观测资料确定的,是大地水准面重力位的平均值。由于海面地形、局部地质环境等因素的影响,局部地区验潮站的平均海平面与大地水准面并不重合,存在一定的差异[10]。因此,局部高程基准与全球高程基准的垂直偏差,实质上是局部地区验潮站的平均海平面与大地水准面之间的重力位差。
对于我国高程基准相对大地水准面的垂直偏差,不少学者作了探索和研究。文献[12—14]利用EGM96模型和GPS/水准数据采用异常位法、高程异常等方法获得我国高程相对大地水准面的垂直偏差0.26 m;文献[15]利用EGM2008模型和全国GPS/水准数据获得我国高程基准相对大地水准面的垂直偏差0.32 m;文献[16—18]对我国高程基准与全球高程基准统一从理论、方法和实际问题等方面做出了一系列研究。但是,因验潮站平均海平面位置特殊,直接测量其坐标程序和工作比较复杂,至今尚未有直接采用验潮站平均海平面处的坐标计算获得的我国高程基准的垂直偏差。
为了获得我国高程基准的第一手资料(曾获得过概略经纬度,与本文测量结果相差十几米),笔者进行了相关测量,然后进行高程基准偏差计算。基本思路是:直接通过大港验潮站坐标利用重力场模型计算我国高程基准的重力位,将计算得到的重力位与IERS给出的大地水准面重力位作差,从而得出我国高程基准的垂直偏差。
本文首先给出通过大港验潮站坐标确定我国高程基准垂直偏差的基本原理,然后介绍测定大港验潮站平均海面坐标的方法及过程,接下来通过重力场模型计算出大港验潮站重力位,进而推算出我国高程基准的垂直偏差,并与我国东部地区GPS/水准数据的计算结果进行了比较,最后给出几点结论。
1 通过大港验潮站坐标确定我国高程基准的垂直偏差

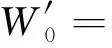
(1)
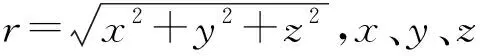
得到高程基准面的重力位后,即可由式(2)得到高程基准的垂直偏差[12-13,15]
(2)

2 大港验潮站平均海面坐标的测定
图1为大港验潮站示意图,验潮井口近似圆形,上面盖以格网铁盘,井口上两个验潮仪连接绿色和黄色两根线,这两根摆线与平均海平面处的交点即为1985国家高程基准的零点。井口两侧有两个水准墩,两水准墩连接一根铜线,铜线距离水准零点6 m,1985国家高程基准的平均海面距离水准零点2.429 m[2]。
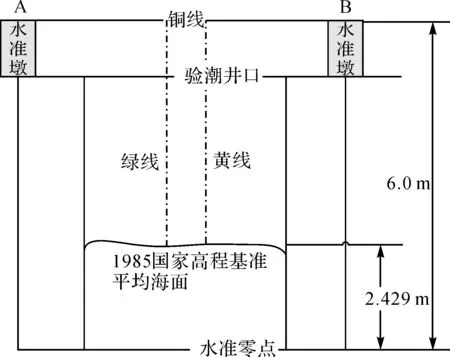
图1 大港验潮站示意图Fig.1 Dagang Tidal Gauge
高程基准的零点坐标无法进行直接测量,只能通过联测得到。
选取验潮站北20 m草地处已有GPS点作为主控点QDYC,在码头灯塔附近选取方位点YCF1和YCF2,在验潮站门口处选取两个过渡点P1、P2,这5个点组成控制网,见图2。

图2 验潮站坐标测量示意图Fig.2 Measurement for the coordinates of Dagang Tidal Gauge
控制网测量采用GPS测量方法实施,使用3台Topcon GPS接收机同步观测,其中主控点QDYC、方位点YCF2按照B级要求进行同步观测,方位点YCF1测量按照C级要求与主控点进行同步观测。
通过水平角测量、距离测量将主控点和方位点平面坐标通过P1、P2、水准墩A和B归算到绿线和黄线处;然后通过高差测量获得主控点和方位点与水准墩A和B之间的高差。
采用Gamit软件、利用4个国际IGS站(BJFS、SUWN、SHAO、WUHN)的观测数据和坐标解算出主控点QDYC和方位点YCF2的坐标;使用Pinnacle软件,利用主控点QDYC和方位点YCF2的坐标解算出方位点YCF1的坐标;使用平差之星2007软件中水准网平差模块,解算出水准墩A和B的大地高;使用平差之星2007软件中网平差模块,解算出黄线、绿线、水准墩A和B的平面坐标;根据水准墩A和B铜线的大地高,减去3.571 m(6 m-2.429 m),即得到黄线、绿线在平均海面处的大地高,从而获得大港验潮站平均海面处的坐标。
GPS网平差解算获得的内符合精度在水平方向分别为1.6 mm、1.5 mm,高程方向为2.2 mm。根据长基线网平差结果统计,外符合精度水平方向1~2 cm,高程2~3 cm,归心测量和水准测量的精度都是毫米级,可以认为通过本文方法测量获得的验潮站坐标精度优于5 cm。
3 结果及分析
采用EGM2008模型和EIGEN-6C4模型分别计算大港验潮站重力位,两个模型的有关参数[23-25]见表1。这里需要说明的是,我国采用CGCS2000参考椭球,椭球参数与EGM2008模型和EIGEN-6C4模型相差甚微,引起的重力位计算差异小于0.05 m2/s2,可以忽略。

表1 EGM2008模型和EIGEN-6C4模型参数
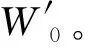

表2 利用大港验潮站坐标计算的我国高程基准的重力位

(3)
式中,WP为地面任一点的重力位,用式(1)重力位模型计算获得;H*是P点的正常高;γm是P点的平均正常重力,由式(4)获得[9]
(4)

将936个GPS/水准数据划分为两组计算:
组1:我国东部GPS/水准数据(经度大于117°E,共计267个点),如图3所示。

图3 东部GPS/水准数据Fig.3 GPS/Leveling data from eastern area
组2:全部GPS/水准数据(936个点)。

表3 两组数据获得的的平均值、离散度和标准差

图4 组1数据计算得到的 obtained from group 1 data

图5 组2数据计算得到的 obtained from group 2 data
所采用的这些GPS/水准数据是在20世纪观测的,其中少数点的三维位置坐标存在较大误差,按照3倍中误差剔除异常值,结果如表4所示。

表4 两组数据获得的的平均值、离散度和标准差(去掉异常值)

表5给出在验潮站直接测定和用东部GPS/水准数据得到的我国高程基准相对大地水准面的垂直偏差。从表5可看出,尽管EIGEN-6C4模型的计算精度要好于EGM2008模型,但是用该模型计算的垂直偏差与用东部GPS/水准数据计算的结果相差较大,而利用EGM2008模型的计算结果与东部GPS/水准数据的计算结果相差较小,因此认为利用EGM2008模型的计算结果更加可靠。
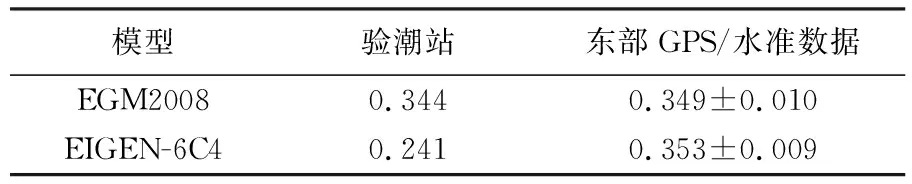
表5 我国高程基准相对全球大地水准面的偏差
利用EGM2008模型和验潮站坐标获得的偏差值是0.344 m,利用东部261个GPS/水准点数据计算获得的偏差值是0.350 m,两者相差0.006 m。
4 结 论
本文通过大港验潮站坐标分别采用EGM2008模型和EIGEN-6C4模型计算得到的我国高程基准相对大地水准面的垂直偏差,并与我国东部261个GPS/水准点数据的计算结果进行了比较,得出如下结论:
(1) 尽管EIGEN-6C4模型精度要高于EGM2008模型,但是利用EGM2008模型和验潮站坐标计算的我国高程基准的垂直偏差与其他数据的计算结果相差较小,因此认为利用EGM2008模型的计算结果要更可靠一些(此结论依赖于已有的GPS/水准数据的计算结果,读者可以有不同的见解,但是文中的计算结果是忠实于数据的)。
(2) 将GPS/水准数据分成东部数据和全国数据两类,东部地区相较于西部地区的得到的重力位更加可靠。
(3) 利用EGM2008模型和大港验潮站坐标计算获得的我国高程基准相对于大地水准面的偏差为0.344 m,比利用东部261个GPS/水准点数据得到的偏差值小约0.006 m。
致谢:感谢有关单位对大港验潮站进行的GPS测量、水平角测量、距离测量和水准测量,并进行数据处理。
