Inequalities for LpMixed Intersection Bodies
2018-10-26
(School of Mathematics and Computational Science,Hunan University of Science and Technology,Xiangtan,411201,China;Department of Mathematics,Tongji University,Shanghai 200092,China)
Abstract:Haberl and Ludwig defined the notions of Lpintersection bodies.In this paper,we introduce the Lpmixed intersection bodies,and establish some geometric inequalities for Lpmixed intersection bodies.Furthermore,the Busemann-Petty type problem for Lpmixed intersection bodies are shown.
Key words:Star body;Radial function;Lpmixed intersection bodies;LpCosine transform 2000 MR Subject Classification:52A40,52A20
§1. Introduction
The unit ball and its surface in Euclidean n-space Rnare denoted by B and Sn−1,respectively.The radial function ρK:Sn−1→ [0,∞)of a compact star-shaped about the origin,K ∈Rn,is defined,for u∈Sn−1,by

If ρK(·)is positive and continuous,then K is called a star body about the origin.The set of star bodies about the origin in Rnis denoted by Sn.The subset of Snthat contains the origin-symmetric star bodies shall be denoted by.Obviously,for K,L∈Sn,

The notions of intersection bodies was introduced by Lutwak[21].The intersection body,IK,of K is the star body whose raidal function in the direction u ∈ Sn−1is equal to the(n−1)-dimensional volume of the section of K by u⊥,the hyperplane orthogonal to u,i.e.,for all u∈ Sn−1,
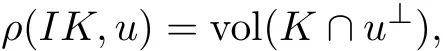
where vol denotes(n−1)-dimensional volume.
Intersection bodies have attracted increased interest during past two decades(see[2,5,7,11-20,23,30]). In particular,intersection bodies turned out to be critical for the solution of the Busemann-Petty problem(see[3,4,6,31]).Haberl and Ludwig[10]extended the classical intersection bodies to Lpspace,and defined the notion of Lpintersection bodies.For K∈Sn,p<1,p 60,the Lpintersection body,IpK,of K is the origin-symmetric star body,whose radial function is defined by,for all u∈ Sn−1,
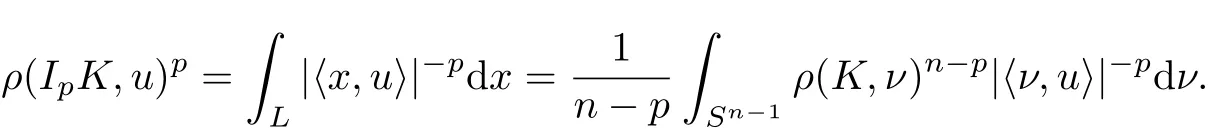
Haberl and Ludwig[10]pointed out that the intersection body IK,of K is obtained as a limit of Lpintersection body IpK of K,that is for all u ∈ Sn−1,
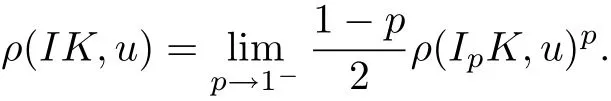
The famous Busemann theorem shows that the intersection body of an origin-symmetric convex body is convex(see[5]).Beck[1]proved that the Lpintersection body of an originsymmetric convex body is also convex.Haberl[9]studied the Busemann-Petty type problem for Lpintersection bodies.Haberl and Ludwig[10]established a characterization of Lpintersection bodies.More results can be found in[22-24,28-29].In[28],Yuan and Cheung obtained the following results.
Theorem A Let K and L be star bodies in Rn,and 0 If p<0,then the inequality(1.3)is reversed.In both cases equalities hold if and only if K and L are dilates. Theorem B Let K be a Lpintersection body and L be a star body in Rn.If then and In both cases equalities hold if and only if K=L. Theorem C Let K be an origin-symmetric star body and L be a star body in Rn.If then and In both cases equalities hold if and only if K=L. In this paper,we define the notion of Lpmixed intersection bodies.Let K∈Sn,p<1,p ≠0,and 0≤i≤n−1.The Lpmixed intersection body,Ip,iK,of K is the origin-symmetric star body,whose radial function is defined by,for all u∈ Sn−1, In particular,if i=0,then Ip,iK is just the Lpintersection body IpK. The main purpose of this paper is to establish above three theorems from Lpintersection bodies to Lpmixed intersection bodies.Our mian results can be stated as follows. Theorem 1.1 Let K and L be star bodies in Rn,and 0 If p<0,then the inequality(1.5)is reversed.In both cases equalities hold if and only if K and L are dilates. Theorem 1.2 Let K be a Lpmixed intersection body and L be a star bodies in Rn.For 0≤i≤n−1,If then and In both cases equalities hold if and only if K=L. Theorem 1.3 Let K be an origin-symmetric star body and L be a star bodies in Rn.For 0≤i≤n−1,if then and In both cases equalities hold if and only if K=L. The set of real-valued,continuous functions on Sn−1will be denoted by C(Sn−1).The subset of C(Sn−1)that contains the even functions will be denoted by Ce(Sn−1).The subset of Ce(Sn−1)that contains the nonnegative functions shall be denoted by(Sn−1).If f,g ∈C(Sn−1),then hf,gi is defined by For f ∈ C(Sn−1)and p<1,p ≠0,the L−pcosine transform,C−pf,of f is defined by(see[8]) for u∈ Sn−1. It is well known that the linear transformation C−p:C(Sn−1)→ C(Sn−1)is self-adjoint,i.e.,if f,g∈ C(Sn−1),then Applying(1.4)and(2.2),we have that For K,L ∈ Sn,λ,µ ≥ 0,p ∈ R and p ≠0,the Lpradial sum λ··L is the star body defined by For K∈Sn,0≤i≤n−1,the dual mixed quermassintegral(K,L)has the following integral representation: By using the Minkowski’s integral inequality,we have the following Lpdual Brunn-Minkowski inequality.For K,L ∈ Sn,0≤ i≤ n−1,and λ,µ ≥ 0,then and In both cases equalities hold if and only if K and L are dilates. The Lpdual mixed quermassintegral(K,L)is defined by(see[25]) In fact,The Lpdual mixed quermassintegral(K,L)has the following integral representation: From an application of the H¨older inequality,one can get the dual Minkowski inequality for Lpdual mixed quermassintegrals.For K,L∈Sn,0≤i≤n−1.Then However, enough cattle were left to make the young man rich, and he and his wife lived happily together, except that every now and then the girl vanished from his sight, and never told him where she had been and In both cases equalities hold with equality if and only if K and L are dilates. For K∈Sn,0≤i≤n−1,and p ≠n−i,we defineby By(2.5)and(2.9),we have that if K,L,M ∈ Sn,0≤ i≤ n−1,p ≠n−i,and λ,µ≥ 0,then From(2.12)and(2.13),it follows that for K∈Sn,0≤i≤n−1,p ≠n−i,and M∈, An immediate consequence of the Lpdual Brunn-Minkowski inequality is obtained.For K∈Sn,0≤i≤n−1.If 0 In fact,we will prove the following Lpdual Brunn-Minkowski inequality which is more general than Theorem 1.1. Theorem 3.1 Let K and L be star bodies in Rn,0≤j≤n−1,0≤i≤n−2,and 0 If p<0,then the inequality(3.1)is reversed.In both cases equalities hold if and only if K and L are dilates. Proof If 0 From the equality condition of Minkowski’s integral inequality,equality holds in(3.1)if and only if K and L are dilates. The special case q=1 of Theorem 3.1 states as follows: Corollary 3.2 Let K and L be star bodies in Rn,0≤j≤n−1,0≤i≤n−2.If 0 If p<0,then the inequality is reversed.In both cases equalities hold if and only if K and L are dilates. Remark 3.3 The case j=0 of Lemma 3.2 is just Theorem 1.1. Lemma 3.4 Let K,L∈Sn,0≤i≤n−1,and p<1,p ≠0.Then Proof From(2.9),(1.4)and Fubini’s theorem,it follows that Remark 3.5 The case i=0 of Lemma 3.4 was established by Yuan and Cheung[24]. Proof of Theorem 1.2 Since K is a Lpmixed intersection body,there exists a star body M such that K=Ip,iM.Using Lemma 3.4 and the fact that if 0≤i≤n−1,the Lpdual mixed volumeis monotone with respect to set inclusion when 0 Applying the dual Minkowski inequality(2.10),we obtain with equality if and only if K and L are dilates.Obviously,if=,we must have K=L. Similarly,we can obtain that the reverse inequality for p<0. Theorem 3.6 If K ∈Snis a star body which is not origin-symmetric in Rn,0≤i≤n−1,then there exists an origin-symmetric star body L,such that but and Proof By(1.4)and(2.5),for K,L ∈ Sn,and λ,µ ≥ 0,we have If K∈Sn,then from(2.12)and(3.2),it follows immediately that Since K is not origin-symmetric and 0 and Similarly,we can obtain that if p<0,then Ip,iK⊆Ip,iL implies(K)<(L).This completes the proof. Lemma 3.7 If K,L∈S,0≤i≤n−1,and p<1,p ≠0,then if and only if Proof From(2.15)and(3.3),we see that we may assume that K,L∈. We first assume that(3.5)holds for all M ∈.Let f∈(Sn−1),and define M ∈by From(2.9),(2.1),(3.6),(2.3)and(2.4),we have Similarly, Hence,from(3.5),we have But this must hold for all f ∈ Ce(Sn−1),since we can write an arbitrary function in Ce(Sn−1)as the difference of two functions in(Sn−1).If we takefor f,we obtain Hence Ip,iK=Ip,iL. On the other hand,let Ip,iK=Ip,iL.Suppose M ∈is such that ρM∈ C−p(Ce(Sn−1))and hence there exists f ∈ Ce(Sn−1),such that From(3.7),(3.8)and note the fact Ip,iK=Ip,iL,we have Proof of Theorem 1.3 Since K∈,let M=K in Lemma 3.7,we have By(2.9)and(2.10),we have,for 0 with equality if and only if K and L are dilates.Obviously,if(K)=(L),we must have K=L.In the same way,we can get the reverse inequality for p<0.












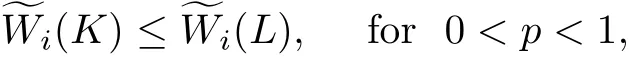

§2.Notation and Background Material

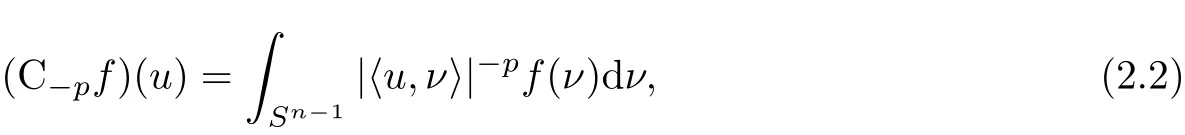
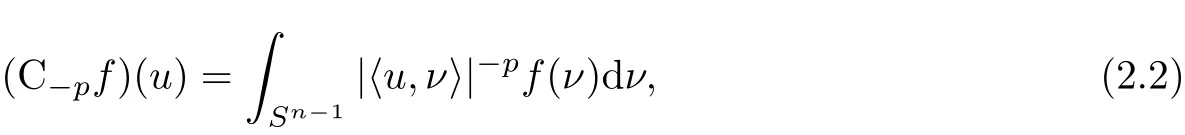

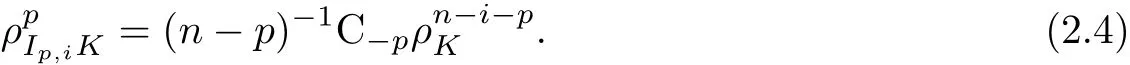











§3.Main Results

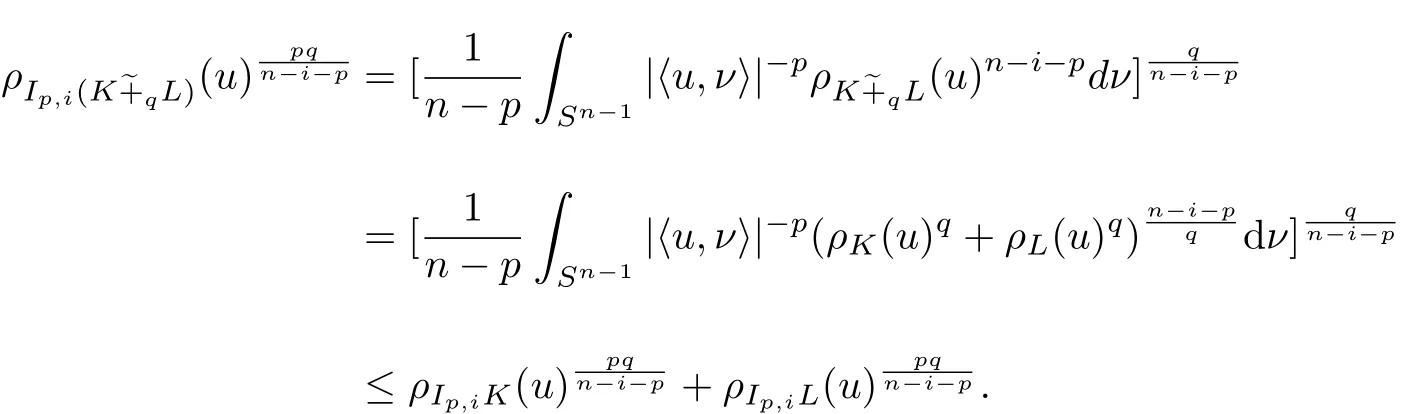




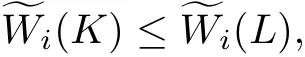

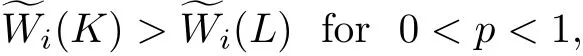


















杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Admissible Periodic Bouncing Solutions for A Class of Semi-linear and Non-conservative Impact Oscillators
- Bayesian Inference on Type-I Progressively Hybrid Competing Risks Model
- Some Basic Properties for Certain Classes of p-valent Analytic Functions Using Di ff erential Operator
- A Note on the Matching Polynomials of Paths and Cycles
- The Lattice of(∈,∈ ∨ qk)-fuzzy Filters in a Given R0-algebra
- Existence and Uniqueness of Almost Periodic Solutions for Some In finite Delay Integral Equations
