The Lattice of(∈,∈ ∨ qk)-fuzzy Filters in a Given R0-algebra

(Department of Mathematics and Statistics,Chifeng University,Chifeng,Inner Mongolia,024000,China)

Abstract:The purpose of this paper is to further study the(∈,∈ ∨ qk)-fuzzy filter theory in R0-algebras.Some new properties of(∈,∈ ∨ qk)-fuzzy filters are given.Representation theorem of(∈,∈∨qk)-fuzzy filter which is generated by a fuzzy set is established.It is proved that the set consisting of all(∈,∈∨qk)-fuzzy filters on a given R0-algebra,under the partial order v,forms a complete distributive lattice.

Key words:Fuzzy logic;R0-algebra;(∈,∨qk)-fuzzy filter;Lattice

§1. Introduction

To make the computers simulate beings in dealing with certainty and uncertainty in information is one important task of artificial intelligence.Logic appears in a “sacred” (resp.,a“profane”)form which is dominant in proof theory(resp.,model theory).The role of logic in mathematics and computer science is twofold–as a tool for applications in both areas,and a technique for laying the foundations.Nonclassical logic[1]including many-valued logic and fuzzy logic takes the advantage of classical logic to handle information with various facets of uncertainty[2],such as fuzziness and randomness.At present,nonclassical logic has become a formal and useful tool for computer science to deal with fuzzy information and uncertain information.R0-algebra is an important class of non-classical fuzzy logical algebras which was introduced by Wang in[3]by providing an algebra proof of the completeness theorem of the formal deductive system L∗.From then,R0-algebra has been extensively investigated by many researchers.Among them,Jun and Liu studied filters in R0-algebras in[4].The concept of fuzzy sets is introduced firstly by Zadeh in[5].Liu and Li in[6]proposed the concept of fuzzy filters of R0-algebras and discussed some their properties by using fuzzy sets theory.As a generalization of the notion of fuzzy filters,Ma et al.dealt with the notion of(∈,∈∨q)-fuzzy filters and investigated their properties in R0-algebras[7].In[8],Jun et al.introduced a more general notion of(∈,∈ ∨ q)-fuzzy filters,named(∈,∈ ∨ qk)-fuzzy filters,and investigated their related properties.At the same time,some results about(∈,∈ ∨ q)-fuzzy filters and(∈,∈ ∨ qk)-fuzzy filters in other logic algebras also have been obtained by many scholars[9−15].

In this paper,we will further research the properties of(∈,∈∨qk)-fuzzy filters in R0-algebras.The rest of this article is organized as follows.In Section 2,we review related basic knowledge of R0-algebras and fuzzy sets.In Section 3,we give several new properties of(∈,∈ ∨ qk)-fuzzy filters.In Section 4,we firstly introduce the concept of(∈,∈∨qk)-fuzzy filter which is generated by an fuzzy set and establish its representation theorem.And then,we investigate the lattice structural feature of the set containing all of(∈,∈ ∨ qk)-fuzzy filters in a given R0-algebra.Finally,we conclude this paper in Section 5.

§2. Preliminaries

Definition 2.1[1]Let M be an algebra of type(¬,∨,→),where¬ is a unary operation,∨and → are binary operations.(M,¬,∨,→,1)is called an R0-algebra if there is a partial ordersuch that(M,,1)is a bounded distributive lattice with the greatest element 1,∨is the supremum operation with respect to,¬is an order-reversing involution,and the following conditions hold for every a,b,c∈M:

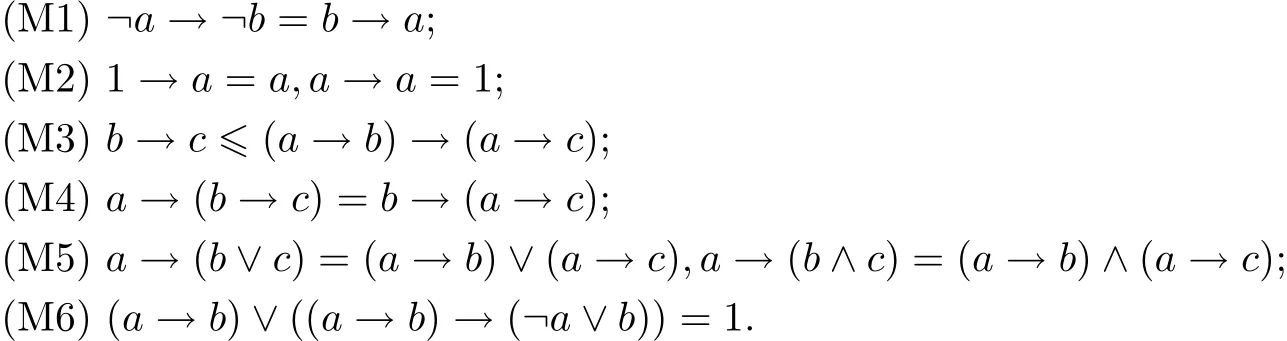
Lemma 2.2[1]Let M be an R0-algebra,a,b,c∈M.Then the following properties hold.

Lemma 2.3[1]Let M be an R0-algebra.Define a new operator⊗on M such that a⊗b=¬(a→¬b),for every a,b,c∈M.Then the following properties hold.

In the unit interval[0,1]equipped with the natural order,∨=max and∧=min.Let X∅,A mapping f:X→[0,1]is called a fuzzy set on X(see[5]).Let f and g be two fuzzy sets on X.We define f∩g and f∪g as follows:

Let X be a non-empty set,x∈X and t∈(0,1].A fuzzy set f on X with the form

for all y∈X,is said to be a fuzzy point with support x and value t and is denoted by xt.For a fuzzy point xtand a fuzzy set f on X,xtis said to belong to(resp.be quasi-coincident with)the fuzzy set f,written as xt∈f(resp.xtqf),we mean that f(x)>t(resp.f(x)+t>1).And to say that xt∨qf(resp.xt∈∧qf),we mean that xt∈f or xtqf(resp.xt∈f and xtqf).

§3. On(∈,∈ ∨ qk)-fuzzy Filters in R0-algebras

According to[8],we let k denote an arbitrary element of[0,1)if no other statements.And for any fuzzy set f on non-empty set X,we let that:

Definition 3.1[8]Let M be an R0-algebra.A fuzzy set f on M is said to be an(∈,∈∨qk)-fuzzy filter of M,if it for all t,r∈(0,1]and a,b∈M,it satisfies the following conditions:

The set of all(∈,∈ ∨ qk)-fuzzy filters of M is denoted by FFil(M).

Lemma 3.2[8]Let M be an R0-algebra.A fuzzy set f on M is an(∈,∈∨qk)-fuzzy filter of M if and only if it satisfies the following conditions:

Lemma 3.3[8]Let M be an R0-algebra.A fuzzy set f on M is an(∈,∈∨qk)-fuzzy filter of M if and only if it satisfies the following conditions:

Definition 3.4 Let M be an R0-algebra and f a fuzzy set on M.A fuzzy set fλon M is defined as follows:

for all a∈ M,where λ ∈ [0,1].

Theorem 3.5 Let M be an R0-algebra and f∈FFil(M).Then fλ∈FFil(M)for all λ∈[0,1].

Proof Firstly,for all a,b∈M,let a 6 b,we consider the following two cases:

(i)Assume that b=1.If a=1,we have that

(ii)Assume that b ≠1,then a ≠1.It follows that

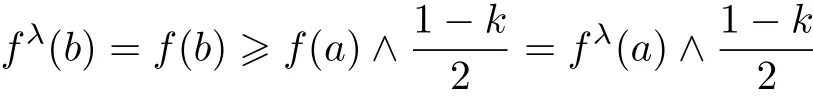
from f∈FFil(M)and(FF3).

Summarize these two cases,we conclude that a 6 b implies fλ(b)>fλ(a)∧,for all a,b∈M.i.e.,fλsatisfies(FF3).

Secondly,for all a,b∈M,we consider the following two cases:

(i)Assume that a⊗b=1.If a=b=1,it is obvious that

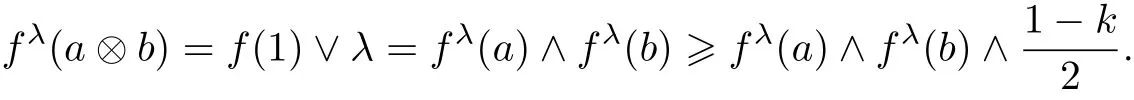
If a=1,b ≠1 or a ≠1,b=1,then a⊗b ≠1,it is a contradiction.

If a ≠1 and b ≠1,it follows that

from f∈FFil(M),(FF4)and(1).

(ii)Assume that a⊗b ≠1.If a=b=1,it is obvious a contradiction.

If a=1,b ≠1 or a ≠1,b=1,let’s assume that a=1,b ≠1,then a⊗b= ¬(1 → ¬b)=b,and so

If a ≠1 and b ≠1,it follows that

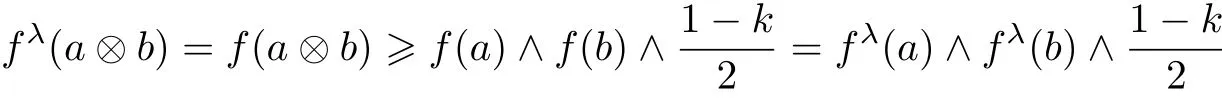
from f∈FFil(M)and(FF4).

Summarize these two cases,we conclude that fλ(a ⊗ b)>fλ(a)∧ fλ(b)∧,for all a,b∈M.i.e.,fλsatisfies(FF4).

Thus it follows that fλ∈ FFil(M)from Lemma 3.2.

Definition 3.6 Let M be an R0-algebra and f,g two fuzzy sets on M.Fuzzy sets fgand gfon M are defined as follows:for all a∈M,

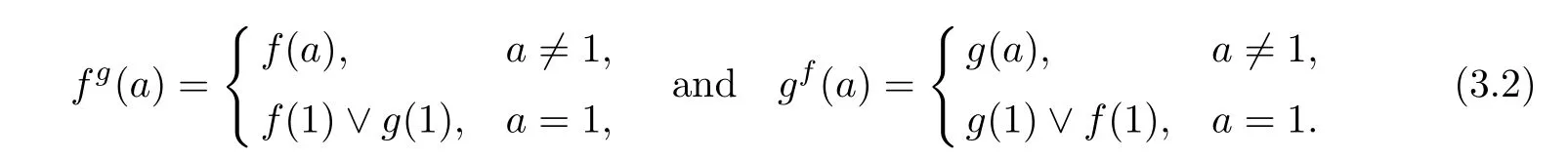
Corollary 3.7 Let M be an R0-algebra and f,g∈FFil(M).Then fg,gf∈FFil(M).

Definition 3.8 Let M be an R0-algebra and f,g two fuzzy sets on M.A fuzzy set f]g on M is defined as follows:for all a,x,y∈M,

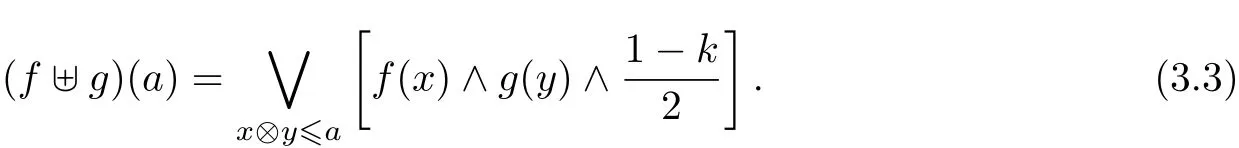
Theorem 3.9 Let M be an R0-algebra and f,g∈FFil(M).Then fg]gf∈FFil(M).

Proof Firstly,for all a,b∈M,let a 6 b,then{x⊗y|x⊗y 6 a}⊆{x⊗y|x⊗y 6 b},and so

Hence fg]gfsatisfies(FF3).Secondly,for all a,b∈M,we have that

and so fg]gfalso satisfies(FF4).Hence fg]gf∈FFil(M)by Lemma 3.2.

§4. The Lattice of(∈,∈ ∨ qk)-fuzzy Filters in a Given R0-algebra

In this section,we investigate the lattice structural feature of the set FFil(M).

Definition 4.1 Let M be an R0-algebra and f,g two fuzzy sets on M.The binary relationis defined as follows:

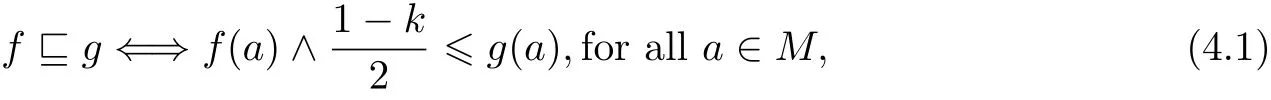
and

Remark 4.2 Let M be an R0-algebra and f,g two fuzzy sets on M.Then according to Definition 4.1,we have that

At the same time,it is easy to verify that the following assertions are hold:

Definition 4.3 Let M be an R0-algebra and f a fuzzy set on M.The intersection of all(∈,∈∨ qk)-fuzzy filters of M containing f is called the generated(∈,∨qk)-fuzzy filter by f,denoted hfi.

Theorem 4.4 Let M be an R0-algebra and f a fuzzy set on M.A fuzzy set g on M is defined as follows:

Proof Firstly,we prove that g∈FFil(M).For all a,b∈M,let a 6 b,then

Thus g satisfies(FF3).Assume that there are x1,x2,···,xn∈ M and y1,···,ym∈ M such that x1⊗x2⊗···⊗xn6 a and y1⊗y2⊗···⊗ym6 b,we have that x1⊗x2⊗···⊗xn⊗y1⊗y2⊗···⊗ym6 a⊗b by(P11).Thus,we can obtain that

Hence f also satisfies(FF4).It follows from Lemma 3.2 that g∈FFil(M).

Secondly,For any a ∈ M,it follows from a 6 a and the definition of g that f(a)∧6 g(a).This means that fg.

Finally,assume that h∈FFil(M)with f v h.Then for any a∈M,we have

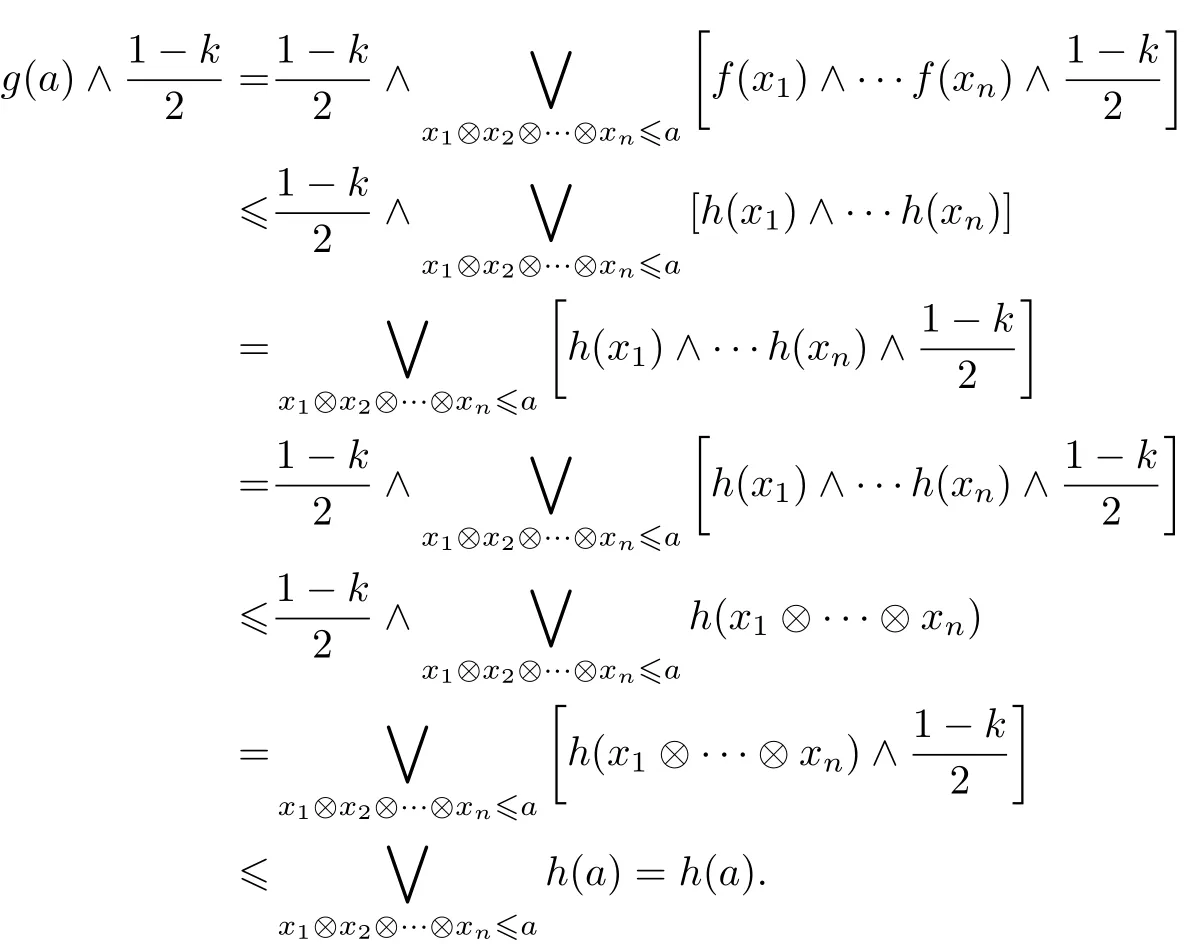
Hence g v h holds.To sum up,we have that g=hfi.

Theorem 4.5 Let M be an R0-algebra.Then(FFil(M),v,0M,1M)is a complete lattice.

Proof For any{fα}α∈Λ⊆ FFil(M),where Λ is an indexed set.It is easy to verify thatis in fimum of{fα}α∈Λ,wherefor all a ∈ M.i.e.,Definesuch thatfor all a ∈ M.Thenis supermun of{fα}α∈Λ,whereis thefilter generated byof M.i.e.,Therefor(FFil(M),v,0,1)is a complete lattice.MM

Ramark 4.6 Let M be an R0-algebra.For all f,g∈FFil(M),by Theorem 4.5we know that f∧g=f∩g and f∨g=hf∪gi.

Theorem 4.7 Let M be an R0-algebra.Then for all f,g∈FFil(M),f∨g=hf∪gi=fg]gfin the complete lattice(FFil(M),v,0M,1M).

Proof For all f,g∈FFil(M),it is obvious that f v fg]gfand g v fg]gf,that is,andfor all a ∈ M.Thus

(i)If a=1,then

(ii)If a<1,then we have

thus fg]gfh for above two cases.

By Definition 4.3 and Theorem 4.4 we have that

Theorem 4.8 Let M be an R0-algebra.Then(FFil(M),,0M,1M)is a distributive lattice,where,f∧g=f∩g and f∨g=hf∪gi,for all f,g∈FFil(M).

Proof To finish the proof,it suffices to show that h∧(f∨g)=(h∧f)∨(h∧g),for all f,g,h∈FFil(M).Since the inequality(h∧f)∨(h∧g)h∧(f∨g)holds automatically in a lattice,we need only to show the inequality h∧(f∨g)(h∧f)∨(h∧g).i.e.,we need only to show thatfor all a∈M.For these,we consider the following two cases:

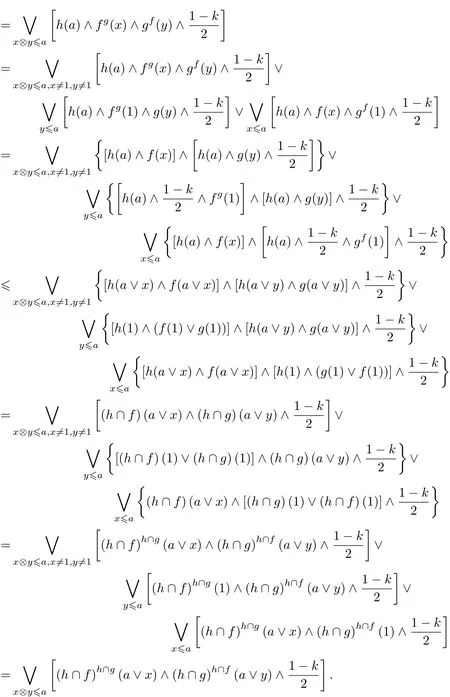
Let a∨x=u and a∨y=v,since x⊗y 6 a,using Lemma 2.3 we get that u⊗v=(a∨x)⊗(a∨y)=((a∨x)⊗a)∨((a∨x)⊗y)=(a⊗a)∨(a⊗x)∨(a⊗y)∨(x⊗y)6 a∨a∨a∨(x⊗y)=a∨(x⊗y)6 a∨a=a.Hence,we can conclude that

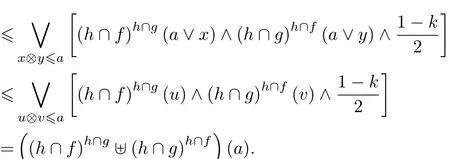
§5.Concluding Remarks

As well known, filters is an important concept for studying the structural features of R0-algebras.In this paper,the(∈,∈∨qk)-fuzzy filter theory in R0-algebras is further studied.Some new properties of(∈,∈∨qk)-fuzzy filters are given.Representation theorem of(∈,∈∨qk)-fuzzy filter which is generated by a fuzzy set is established.It is proved that the set consisting of all(∈,∈∨qk)-fuzzy filters in an R0-algebra,under the partial order,forms a complete distributive lattice.Results obtained in this paper not only enrich the content of(∈,∈ ∨ qk)-fuzzy filter theory in R0-algebras,but also show interactions of algebraic technique and fuzzifying method in the studying logic problems.We hope that more links of fuzzy sets and logics emerge by the stipulating of this work.