A Note on the Matching Polynomials of Paths and Cycles

(Department of Mathematics,Taizhou University,Linhai,317000,Zhejiang,China)

Abstract:The spectra of matching polynomials which are useful in the computations of resonance energy and grand canonical partition functions of molecular’s.It also present other properties for certain classes of graphs and lattices.In[1]Balasubramanian calculates several matching polynomials and matching roots of several molecular graphs.He found that the matching polynomial of C6,C10,C14,C18and C22are divided by x2−2.In this note,we prove that x2−2 divides MC4k+2(x),k=1,2,...,n and obtain some other properties of matching polynomials of paths and cycles.

Key words:Graph algorithms;Matching polynomial;Matching roots;Combinatorial problems

§1. Introduction

All graphs considered in this paper are undirected and simple(i.e.,loops and multiple edges are not allowed).Let G=G(V(G),E(G))be a graph with vertex set V(G)={v1,v2,···,vn}and edge set E(G)={e1,e2,...,em},where|V(G)|=n is the order and|E(G)|=m is the size of G.Let NG(v)denote the neighbor set of vertex v in a graph G.The degree of v in G,denoted by dG(v)or deg(v),is equal to|NG(v)|.Two edges are said to be independent if they are not incident with any common vertex.A matching M is a subset of E(G)in which the edges are pairwise relatively independent.Denote by m(G,k)the number of matchings with k edges.In[2]and[3],D.Cvetkovi´c,etc.denote the matching polynomial:

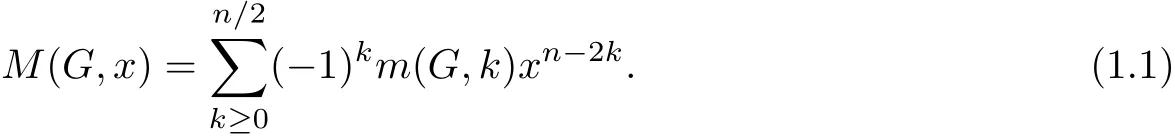
For convenience,we set m(G,0)=1.m(G,1)=|E(G)|is the number of edges.Clearly,m(G,k)=0 if k>n/2.If an edge of M is incident with a vertex of V(G),then we say v is saturated by e.Otherwise,we say v is unsaturated by e.If all vertices of V(G)are saturated by edges of M,then we say M is a perfect matching.

Graph polynomials,such as the characteristic polynomials,Matching polynomial,Independence polynomials and Chromatic polynomials have great interesting.Their largest roots and the coefficients contain many graph structural properties.In[5]authors have characterized several graphs by their chromatic polynomials.In[4],H.L.Zhang studied the matching polynomials of several types of graphs,and give some relations between them.In this note,we prove that x2− 2 divides MC4k+2(x),k=1,2,···,n and obtain some other properties of matching polynomials of paths.

§2. Preliminaries

Let G−v be the graph obtained by deleting a vertex v with incident edges form G.G−e be the graph obtained by deleting an edge e from G.The matching polynomial of a simple graph has the following results.

Lemma 2.1[2]Let G be a graph with u∈V(G),and suppose the neighborhood of u is Γ(u)={v1,v2,···,vk},e=uv ∈ E(G).Then

where e=uv in G.

Lemma 2.2[2−3]Let G1,G2,···,Gkbe k components of G.Then

Lemma 2.3[2−3]Suppose m,n ∈ z+,then the matching polynomials of paths and cycles are:

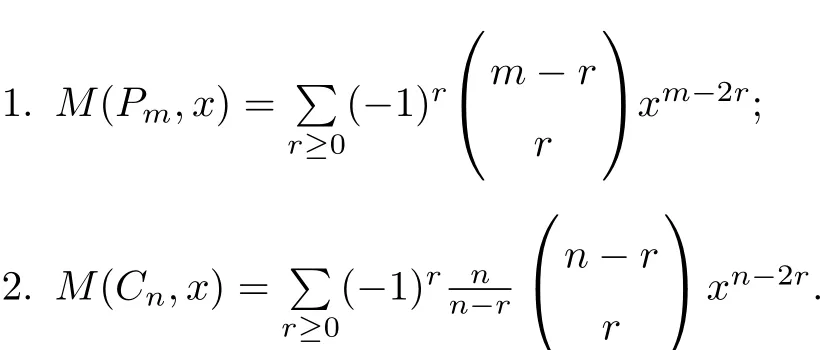
Lemma 2.4[4]Let{gi(x)}be a series of polynomials with intergral coefficients and gn(x)=xgn−1(x)− gn−2(x).Then

1.gn(x)=M(Pk,x)gn−k(x)−M(Pk−1,x)gn−k−1(x);

2.M(Pn,x)|gk(n+1)+i(x)if and only if M(Pn,x)|gi(x).

§3. Main Results

In this section,we give several interesting results on the matching polynomials of paths and cycles.

Theorem 3.1 Let M(Pn,x)be the matching polynomial of Pn.Then

Proof We apply induction on the number of vertices.For a path on small number of vertices,we can easily check it.We only prove on a path on large number of vertices.Suppose that result is correct for Psand Pt,that is M(Ps,2)=s+1 and M(Pt,2)=t+1.Let us think about the path Ps+t(2).By the basic lemma of deleting an edge,we have

by our assumption

Theorem is proved.

Similarly,we have an interesting result for cycles.

Theorem 3.2 Let M(Cn,x)be the matching polynomials of Cn.Then

Proof By Lemma 2.1(3),M(Cn,x)=M(Pn,x)− M(Pn−2,x)and with Theorem 3.1 M(Pn,2)=n+1,hence M(Cn,2)=n+1−(n−1)=2.

Theorem 3.3 Let M(Pi,x)be the matching polynomials of Pi.Then M(Pm,x)|M(Pn,x)if and only if(m+1)|(n+1).

Proof Let n+1=k(m+1).We apply induction on k.When k=1,the theorem holds.Assume that theorem holds when k − 1,that is M(Pm,x)|M(P(k−1)(m+1)−1,).By the Lemma 2.1 we have,

By our assumption the right hand-side of the equation is divided by M(Pm,x).

Hence M(Pm,x)|M(Pn,x).

Now we prove the necessity of theorem.Assume that n=k(m+1)+i,1≤i

Now we give the main result of this note.

Theorem 3.4 Let M(Ci,x)be the matching polynomials of cycle Ci.Then x2−2 divides M(C4k+2,x),k=1,2,...,n.

Proof By Lemma 2.1,we have the matching polynomial of C4k+2is

By Theorem 3.3,M(P3,x)|M(P4k−1,x)and M(P3,x)=x3− 2x.xM(P3,x)|xM(P4k−1,x).Hence the right hand side of equation is divided by x2−2.Therefore(x2−2)|M(C4k+2,x),k=1,2...,n.