基于EEMD-RVM风力发电机故障诊断方法研究*

牛盛瑜，张新燕，杨璐璐，邸强，张冠琪

(新疆大学 电气工程学院，乌鲁木齐 830047)

0 引 言

风电机组多位于野外，要经受大风等外界环境产生的冲击，同时，风电系统内部的变化也会对发电机造成一定的影响，在多种恶劣的工况下运行，发电机出现故障率也急剧上升，导致风机运行的可靠性降低，运行寿命减少。目前，减少风电机组故障率有效措施就是对其进行早期故障诊断，通过分析各类征兆信息来确定故障的部位、程度，从而快速、准确的排除故障。

目前，对风力发电机故障的诊断方法多种多样，主要可以分为：(1)传统诊断方法：如噪声检测[1]、红外线测温等。此类方法的诊断结果都很直观，准确度也比较高，但是对微弱的早期的故障并不能有效地检测出来，同时多依赖于检测者的经验判断；(2)智能诊断方法：如神经网络[2]、遗传算法[3]等。此类方法较节省时间，同时能较准确地对故障进行判断，不过通常需要大量的数据来支撑其诊断的精确度，而发电机的故障不常发生，这意味着能够采集到的故障数据量较少，因此不能保证该类方法诊断的精确度；(3)数学诊断方法：如SVM[4]、混沌分析[5]等。此类方法可以依靠少量的数据对故障进行准确地判断，且随着计算机技术及数学理论的不断发展，此类方法也能不断改进，但此类方法的前期数据处理部分对最终诊断结果的准确性有很大影响，选择适当的数据处理方法便显得十分重要。

针对上述诊断方法存在的故障样本数据量少、诊断结果精确度低等问题。提出了一种运用EEMD结合RVM对风力发电机的四类运行状态(包括正常运行、发电机主轴偏心、发电机轴承磨损和定子绕组匝间短路)进行诊断的方法。将文献[6]中所提LS-SVM结合EEMD的方法，与文献[7]所提WPD结合RVM的方法运用于对风机的四类运行状态进行诊断，并与本文所提方法的诊断结果进行对比得出EEMD-RVM的诊断耗时少、诊断结果准确可靠的结论。从而保证风机能在造成严重损失之前采取必要措施，提高风机运行可靠性，延长运行寿命。

1 EEMD特征提取

风力发电机运行过程中伴随着很多非线性因素，而故障产生之初只对其造成很微弱的影响，使得传统检测方法如快速傅里叶变换(FFT)等不能准确的提取风力发电机的故障特征。本文运用EEMD[8]提取发电机振动信号的故障特征，相对于经验模态分解(EMD)该方法能有效削弱各个IMF分量模态混叠的程度，提取更为准确的故障特征[9]。

EEMD方法过程如下：

(1)对提取的原始信号x(t)加入幅值为K高斯白噪声ni(t)得到式(1)。

xi(t)=x(t)+ni(t)

(1)

式中i表示第i次对原始信号加入白噪声；xi(t)为第i次加入白噪声后的信号；ni(t)为第i次加入的随机的白噪声。

接着对加噪声后的信号xi(t)进行EMD分解，得到式(2)。

(2)

式中Ci,j为第i个加噪信号xi(t)的M个EMD分解中第j个IMF分量；ri为第i次加噪信号EMD分解的余项。

(2)由于高斯白噪声频谱的均值为零，可以消除高斯白噪声时域分布参考结构故可对第j个IMF分量的i个不同的分量求平均值，如式(3)所示。同时对i个余项求取平均值如式(4)所示。

(3)

(4)

(3)最后把M个平均IMF与平均余项相加结合得到信号x(t)的EEMD如式(5)所示。

(5)

2 RVM分类模型

RVM是一种在全概率贝叶斯框架下进行运算的核函数算法[10]。在先验参数的结构下使参数的后验分布趋于零，保留非零参数所对应的点即能够展现样本本质特征的相关向量(Relevance Vectors)。RVM分类模型如下：

设有L个待训练样本集为(xl,tl)(l=1,2,…,L,x∈Rd,t∈{0,1})，式中xl为输入值向量，tl为目标值向量，在二分类问题里t∈{0,1}，RVM分类模式定义为式(6)。

(6)

式中k(x,xl)为核函数；ω为权值向量，ω=(ω1,ω2,…,ωl)T，在给定待训练样本xl(l=1,2,…,L)和目标值tl(l=1,2,…,L)的前提下，确定训练样本对应的权值ω便可构建出RVM分类模型。

首先，把式(6)利用logistic sigmoid函数映射到(0,1)区间上，得到概率分布函数为：

(7)

为所有权值ω定义均值为0，方差为α-1的高斯先验分布：

(8)

式中α为L+1维超参数向量，α=(α0，α1，…，αL)T；N(·)为正态分布函数。

其次，对于一组新的测试样本X*，对应的目标值向量t*，其预测分布概率为：

(9)

利用拉普拉斯二次逼近的方法近似计算P(ω|t,α)和P(α|t)，通过迭代的方法便可得到权值ω和超参数α。

(1)迭代求ωMP，推导如式(10)所示。

g=▽ωlog[P(t|ω)P(ω|α)|=ΦT(t-y)-Aω

(10)

H=▽ω▽ωlog[P(t|ω)P(ω|α)|=-ΦTBΦ-Α

(11)

(12)

式(10)中y=[y1,y2,…,yL]T;Φ=[Φ(x1),Φ(x2),…,Φ(xL)]T;Φ(xl)=[1,k(xl,x1),…,k(xl,xL)]T。式(11)中B=diag(β0,β1,…βL)；βl=[yl(1-yl)]；H是Hessian矩阵。

(2)迭代求αnew得：

(13)

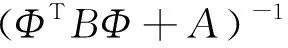
最后，求解得到αnew后重新计算ωMP与∑，重复步骤(1)，步骤(2)，直到达到收敛条件，经过一定的更新后，绝大多数的αl则会趋于一个有限大的定值，这些αl对应的xl的集合为相关向量。

3 基于EEMD-RVM的风力发电机故障诊断方法研究

3.1 运用EEMD-RVM方法对风力发电机故障诊断流程(见图1)

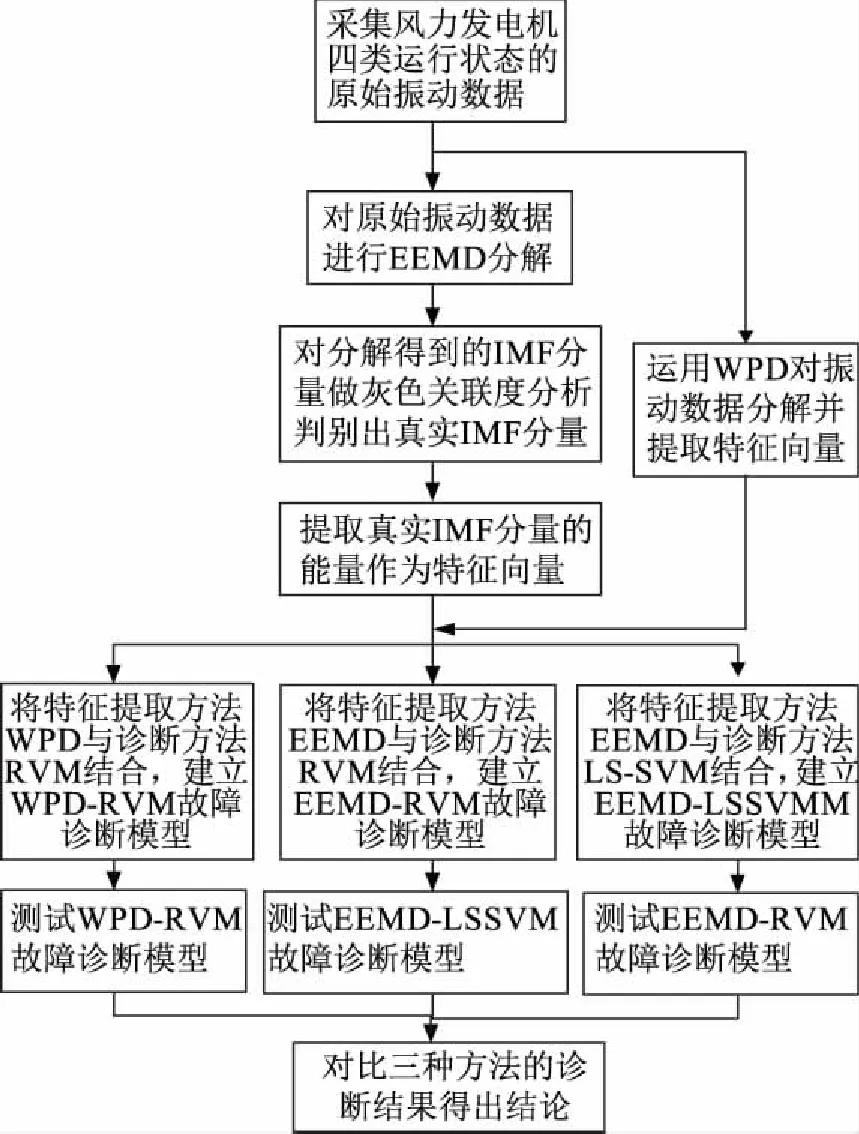
图1 风力发电机故障诊断流程图

(1)风机原始振动运行数据采集。

用于诊断的四类风力发电机运行状态分别为正常运行、发电机主轴偏心、发电机轴承磨损和定子绕组匝间短路，其中正常运行、发电机主轴偏心、发电机轴承磨损三种运行状态采集于新疆大学风能技术实验室SUT-1000型直驱风力发电机试验台；定子绕组匝间短路(5%的绕组短路)下的主轴径向振动由ANSYS软件电-磁-结构耦合仿真结合文献[11]中推导方法得出。采样频率和采样时间分别为1 000 Hz和2 s，4类运行状态下各采集70组数据组数据。图2是风机4 种运行状态下的一组主轴径向振动波形。

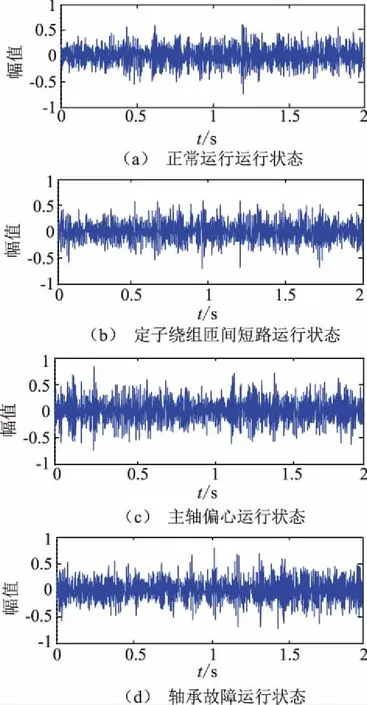
图2 风力发电机4种运行状态下的主轴径向振动信号

(2)EEMD分解参数设定。

文献[8]定义EEMD分解结果e与白噪声的幅值k和加入白噪声次数N的关系式为：

(14)

式中k越小，e随之减小，精确度就越高，但k值过小就无法把原信号内出现的间歇现象消弭。当k给定时，N越大，e越小，越能抵消噪声的干扰并准确的表达原信号的特征[12]，但计算时间也将延长，因此选择合适的白噪声幅值k与白噪声加入次数N是十分重要的。为了兼顾处理速度与精确性，本文参考文献[13]中研究结果设定加入白噪声的次数N=100，加入白噪声的幅值k为原信号x(t)标准差的0.02倍。运用EEMD对图2中正常运行状态进行分解后除去余项得到的各IMF分量如图3所示。

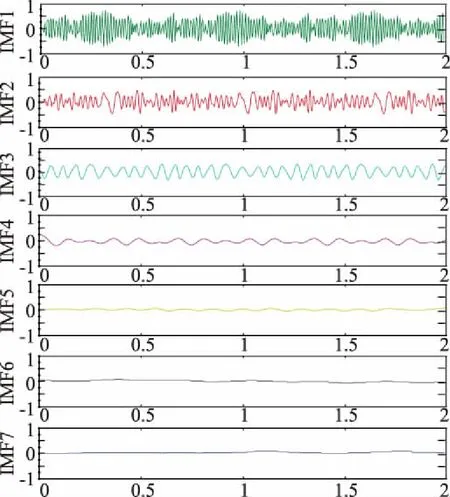
图3 图2中正常运行状态EEMD分解的七个IMF分量

(3)特征向量的提取。

通过EEMD分解后的IMF分量中包含着一些虚假分量，这些虚假分量会影响信号特征的准确性，从而降低诊断精确度。采用灰色B型关联度分析[14]对虚假IMF分量进行识别，可以很好地排除虚假分量，提高诊断精确度。

利用灰色B型关联度分析各IMF分量与原函数的关系，首先，设原函数为xi(k)，待计算的IMF函数分量为xi(k)，k=1,2,…,n，计算公式如下：

(15)

(16)

(17)

(18)

再对经过灰色B型关联度分析的各IMF进行归一化处理，计算公式为：

(19)

式中xnorm为归一化后的值；xmin和xmax分别为本组IMF中的最大值和最小值；x则为待归一化的IMF分量。

对图3中正常运行状态IMF分量进行上述分析，结果如表1所示。

表1 正常运行状态下的灰色关联度分析

通过表1归一化后的数据可以看出前四个IMF分量与原函数的关联度较高，故选定前四个IMF分量做为特征向量，再以同样方法分析其余三组运行状态，并分别提取四种运行状态下关联度较高的IMF分量的能量并归一化，得到其特征向量组如表2所示。

运用WPD分析并分别提取图2中四组运行状态的的特征向量如表3所示。

按照上述两种方法再分别对各类运行状态下的其余69组振动信号的特征向量进行提取，在每种运行状态下采集的70组特征向量数据中任选20组做为RVM的训练样本数据，剩下的50组做为测试样本数据，由于篇幅所限其余69组特征向量数据不再逐一列出。

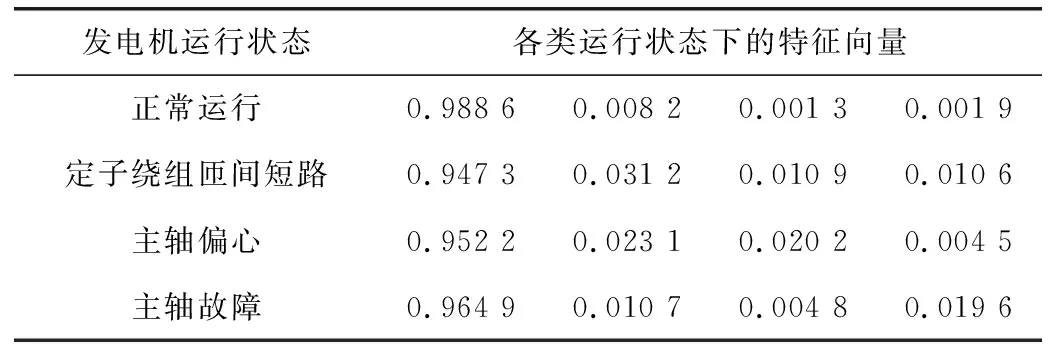
表2 运用EEMD提取的发电机4种运行状态下的特征向量

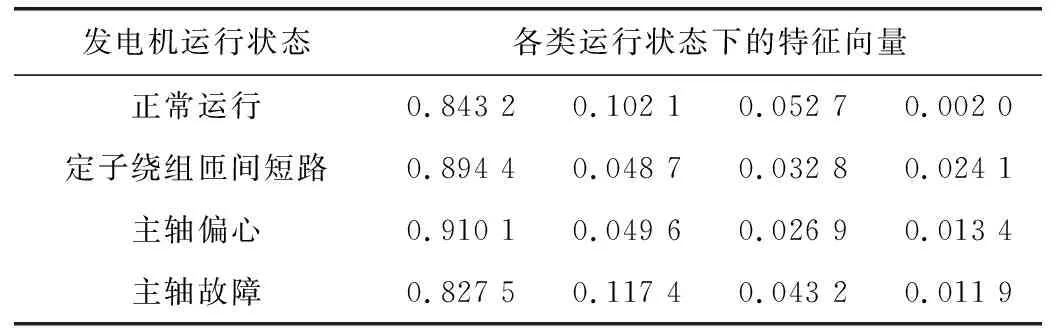
表3 运用WPD提取的发电机4种运行状态下的特征向量

(4)RVM多分类模型的建立及各类参数设定。

RVM是二分类器，对多类事件进行判别时就需要建立RVM多分类模型，为兼顾分类精度高和分类时间短的要求，故选取“有向无环图”多分类模型。“有向无环图”(Direct Acyclic Graph，DAG)[15]模型如图4所示。

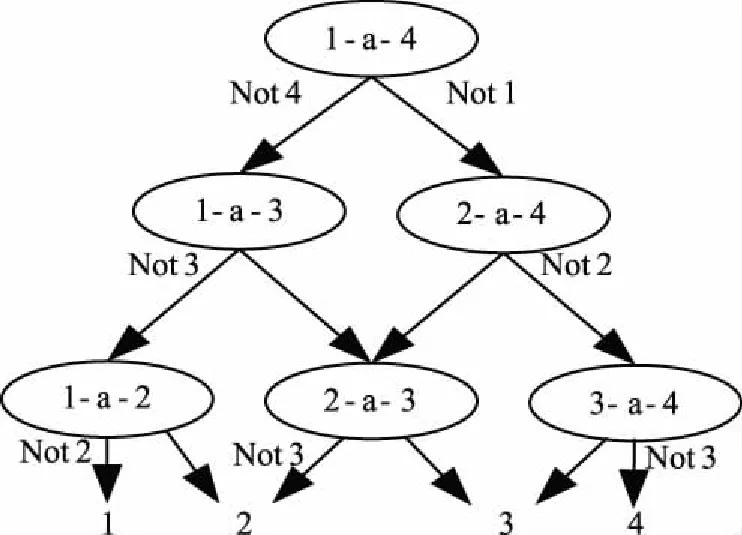
图4 四分类“有向无环图”模型

图4中1、2、3、4分别表示发电机正常运行、发电机主轴偏心、发电机轴承磨损和定子绕组匝间短路四类风机运行状态，每一个节点相当于一个RVM分类器。输入一个分类样本x，先由最上面的根节点开始区分第1类和第4类运行状态，将x代如训练好的RVM分类器中若判别不是第4类则从左边分支进入下一个RVM分类器进行分类判别，若判别不是第1类则从右边分支进入下一个RVM分类器进行分类判别，以此类推直至最后输出指向的数字，代表经过诊断后样本x所属的运行状态。

实验中为了保证实验结果对比的公平性，SVM与RVM的核函数均采用对数据量适应能力强的RBF核函数，核函数宽度参数均取0.5。

3.2 诊断结果及诊断性能对比

分别运用文献[6]中所提分类方法LS-SVM结合本文特征提取方法EEMD与文献[7]所提特征提取方法WPD结合本文分类方法RVM对风机四类运行状态进行诊断，得到的诊断结果与本文所提方法EEMD-RVM的诊断结果进行对比。

首先，用EEMD提取到的任意20组各类运行状态的特征向量作为多分类RVM的训练样本，建立EEMD-RVM诊断模型并用其余50组进行测试，接着对另外两种方法WPD-RVM和EEMD-LSSVM也分别以上述步骤进行诊断仿真测试。我们对50组测试数据分别随机抽取10、20、30、40组以及全部进行诊断(诊断结果如表4所示)。表4中三种方法对正常运行和定子绕组匝间短路下的诊断准确率相对较高，这是因为主轴偏心和轴承磨损运行状态复杂多变，提取的故障特征表达准确度较低，而正常运行和定子绕组匝间短路运行平稳、规律性强，特征向量能很好地表达故障，与此同时，在主轴偏心和轴承磨损运行状态下结合EEMD方法的准确率也较结合WPD方法的高，这更能说明选择好的特征提取方法能够提高诊断准确率。

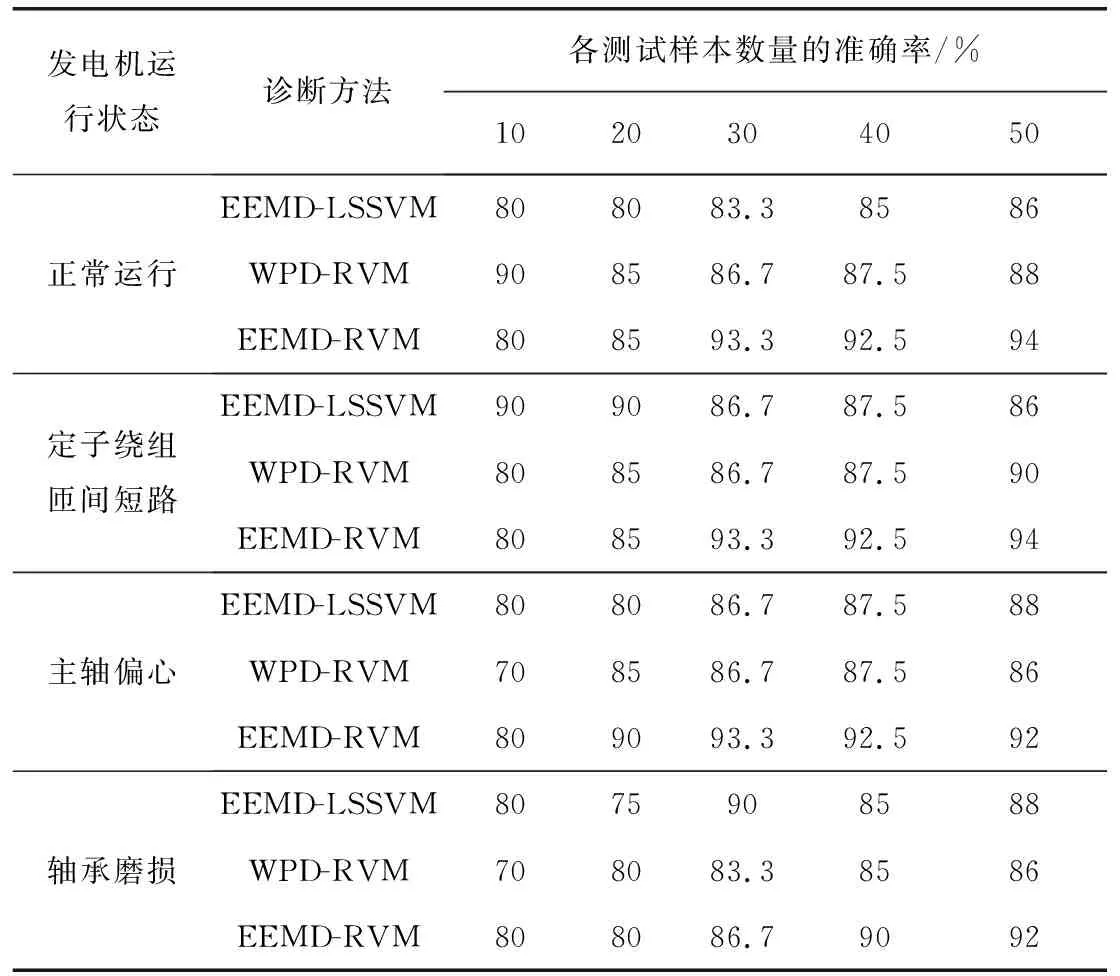
表4 四类运行状态下三种方法的测试结果

图5中所提方法对10组测试数据诊断准确率相对较低，当选取的测试数据增加到30组时EEMD-RVM的准确率较其余两种方法有着显著的升高，此后便保持平稳；其余两种方法的准确率也在30组数据后维持平稳，但准确率低于EEMD-RVM，这是因为样本量少随机性便高，随着测试样本数量的增加，随机性便随之下降，准确率越趋于实际值。

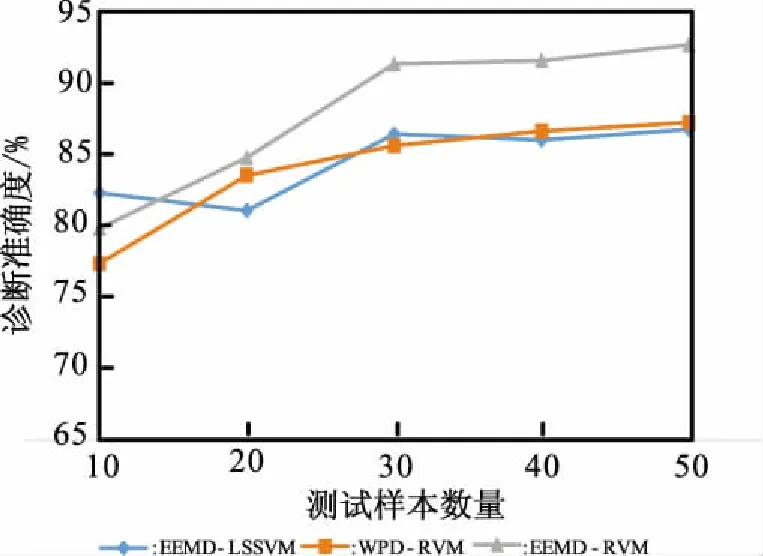
图5 三种方法准确率对比的折线图

分析总体性能对比表5可知：

(1)对比WPD与EEMD两种特征提取方法：WPD-RVM的准确率为87.5%低于EEMD-RVM的93%，训练和测试耗时也是三种方法里最长的，因为WPD对振动信号的去噪能力较差，致使提取到的特征向量表征能力较差，训练耗时长，诊断准确率较低，而EEMD提取的特征向量能较为准确地表达了风力发电机的运行状态；

(2)对比LSSVM与RVM两种诊断方法：EEMD-LSSVM与EEMD-RVM的训练和测试耗时相差无几，但EEMD-LSSVM的50组样本测试平均准确率低于EEMD-RVM，可以看出RVM与LSSVM都具有耗时短的优点、但RVM的诊断准确率高于LSSVM；

(3)三种方法都有着较好的诊断能力，而文中所提方法EEMD-RVM的诊断能力略优于其余两种方法。

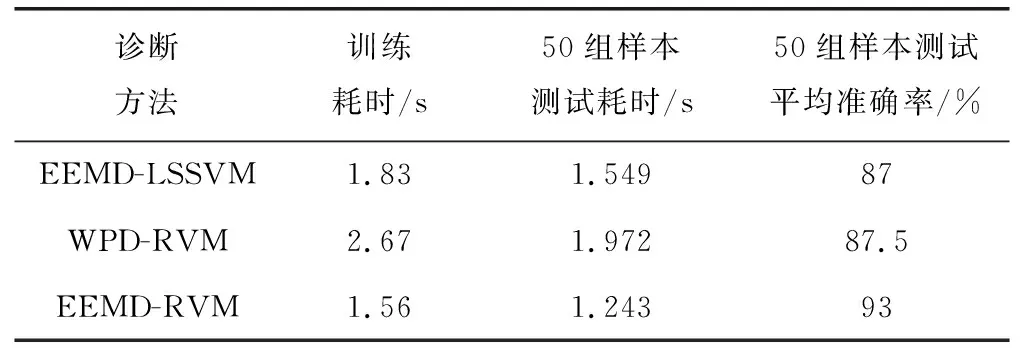
表5 总体诊断性能对比

4 结束语

针对风力发电机早期故障诊断问题提出了一种结合运用EEMD和RVM的方法，通过对采集或仿真得到风力发电机四种运行状态的振动数据处理后搭建故障诊断模型进行诊断测试，并与其余两种方法的诊断结果进行比较得到结论如下：

(1)EEMD能有效解决采集到的原始振动信号模态混叠的问题，再结合灰色关联度法便很好的排除虚假IMF分量，提高特征向量的质量，与WPD相比，其特征向量的表达能力更强，进而缩短诊断时间，增加准确率；

(2)RVM与LSSVM的诊断耗时都较短，但RVM的稀疏性更好、泛化能力强的特点致使其诊断准确率高于LSSVM，且分类结果较为可靠，因此RVM对风力发电机的早期故障的诊断能力更为出色，进而避免故障的进一步恶化，延长风力发电机的寿命，减少维修成本；

(3)EEMD-RVM的诊断时间短、诊断准确率高和诊断结果的可靠等特点能很好的运用在风力发电机故障的实时检测上，但实际运行过程中多变的运行工况会使风机的故障变得难以检测，故障恶化更为迅速，因此，需要通过采集更为详尽的故障训练样本，选择适合的RVM核函数或对RVM多分类模型进行可靠性分析等一些优化手段来提高EEMD-RVM方法的准确率。