基于FSSI的环境激励下机电振荡特征参数快速识别方法研究*
2018-10-25王丽馨
王丽馨
(东北电力大学 电气工程学院,吉林 吉林 132012)
0 引 言
随着电力系统规模的不断增大,低频振荡已成为制约大规模电能远距离外送、威胁现代互联电网安全稳定的关键问题之一。快速准确地获取系统机电振荡模式及模态信息对于大电网安全稳定运行具有重要意义[1]。
电力系统随机响应数据以负荷投切等随机扰动为激励,数据量丰富,且蕴含大量系统实际工况的振荡信息。随着广域测量系统在电力系统中迅速发展,以随机响应数据为基础的低频振荡分析法越来越受到学术界和工程界的广泛关注[2-3]。文献[4]利用频域分解法从随机响应信号中提取振荡频率、阻尼比和模态振型等信息。但对于阻尼良好的系统,该方法无法准确辨识系统阻尼比,同时对于频率接近的模式区分存在困难。Zhou N[5]等人以随机响应数据为基础,利用改进的递归最小二乘法提取系统机电振荡信息。但该方法数值稳定性较差。Khalilinia H[6]等人通过对获得的随机响应数据进行小波尺度分解从而得到系统模态信息。但小波函数及其参数的选择对辨识结果影响较大。随机子空间算法直接作用于时域数据,因而具有较好的频率分辨率,同时在处理数据量较大以及动态过程较复杂的系统方面具有较好的适应性,成为基于量测信息参数辨识的常用方法[7-9]。但现有的随机子空间算法大都需要对高维Hankel矩阵进行SVD分解,计算量大,同时计算过程相对复杂,计算耗时长,严重影响了SSI算法的在线应用。
为了进一步提高随机子空间算法在电力系统机电振荡参数识别方面的计算速率,本文提出了基于快速随机子空间辨识法的电力系统机电振荡参数识别方法。利用LQ分解取代了传统随机子空间算法中的SVD分解过程,在保证模态参数辨识精度的基础上,极大提高了辨识速率。仿真算例表明本文所提方法在保证了辨识精度的同时极大提高了计算速度。
1 环境激励下系统动态响应特征
系统实际运行过程中,负荷波动、新能源有功输出的随机性等均会给系统带来随机扰动。以负荷随机波动为例,电力系统动态模型可以用如下的随机微分代数方程形式描述[10]:
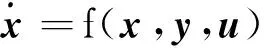
(1)
0=g(x,y,u)
(2)
式(1)为系统微分方程,描述了系统中发电机及相应的控制装置、负荷等的动态过程,式(2)为系统的代数方程,一般由系统潮流方程及发电机、负荷等静态方程组成。f和g为连续函数;x(x∈Rnx)为系统的状态变量,如发电机功角等,y(y∈Rny)为系统的代数变量,如母线电压,母线相角等,u为随机波动变量。
假设负荷随机波动服从(Ornstein-Uhlenbeck,OU)分布,建立负荷随机波动的系统动态模型[11-12]:
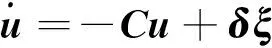
(3)
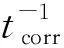
随机扰动过程中,电力系统运行状态未发生变化,即各台发电机运行平衡点不变,则可以通过线性化系统状态来近似分析系统状态变量的动态过程。线性化式(1)~式(3),同时消掉代数变量y,则:
(4)
式中fx、fy分别为式(1)中对应于x、y的雅可比矩阵;gx,gy,gu分别为式(2)中与变量x,y,u对应的雅可比矩阵。
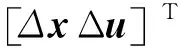
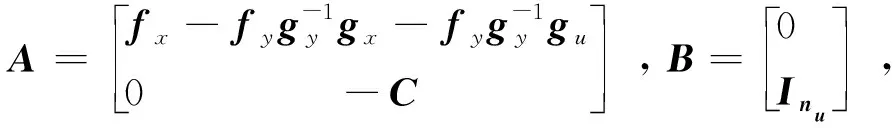
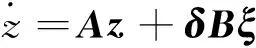
(5)
式(5)即为负荷随机波动下,电力系统线性化状态空间模型。求解得到系统n个振荡模式对应的特征值λi=σi+jωi(i=1, 2, …,n),则系统状态变量的时域解析表达式为:
(6)
一般地负荷随机波动幅值较小,加之系统中调速器等控制器的作用,使得系统状态变量中的振荡分量幅值亦非常小,使得测量得到的系统随机响应信号外在表征为杂乱无章类似噪声的信号。但通过对式(6)分析可知,表面看似杂乱无章的类似噪声的随机响应信号是环境激励驱动下的系统动态响应和量测噪声叠加的类噪声信号,其中蕴含了丰富的电力系统动态信息,采用合适的技术手段可以从中提取系统的机电振荡信息参数,及时掌握系统运行动态。
2 基于FSSI的机电振荡特征参数识别
在实际应用中,量测数据在时间上都是离散的,经离散采样后,可得如下随机状态空间系统[13]:
(7)
式中xk∈Rn为系统状态量;yk∈Rl为测量得到的输出量;wk∈Rn和vk∈Rl均为假定白噪声,且E(wk)=E(vk)=0;A∈Rn×n和C∈Rl×n分别代表系统状态矩阵和输出矩阵;Δt为采样间隔。
对式(7)所示的随机系统,由采样时序数据组成Hankel矩阵:
(8)
式中Yp表示过去时刻数据,Yf为将来时刻数据;H∈R2li×j,i为块矩阵行数,且要大于系统阶数2n;j为Hankel矩阵列数;若l为系统测点个数,则Hankel矩阵共有2li行;若量测数据样本采样点数为r,为了保证所有数据均能被放入Hankel矩阵中,必须满足关系式j=r-2i+1。
高维Hankel矩阵的分解是影响随机子空间辨识方法计算速率的关键因素,传统随机子空间利用SVD分解来处理Hankel矩阵,计算效率较低,影响了随机子空间算法的计算速度。本文引入LQ分解代替SVD分解,有效的提高了计算效率。
将Yf投影到Yp得到正交投影矩阵,即:
Yf/Yp≡YfYp(YpYp)†Yp=Oi
(9)
式中,Oi正交投影矩阵,†表示相应矩阵的伪逆。
利用正交投影计算得到延伸观测矩阵,即:
(10)
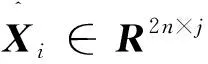
以Hankel矩阵LQ分解来代替式(8)投影计算:
lilij
(11)
(12)
由式(12)可知,L21与Γi列空间是同构的,因此在求得Hankel矩阵LQ分解的下三角矩阵L21后,即可计算出延伸观测矩阵Γi。
进而计算L21奇异值(SVD)分解:
(13)
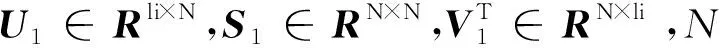
延伸观测矩阵Γi可由矩阵U的前N列确定:
Γi=U1
(14)
计算求得连续系统状态矩阵Ac及输出矩阵Cc:
(15)
(16)

输出矩阵Cc为延伸观测矩阵Γi的第1行,即:
Cc=Γi(1,:)
(17)
连续系统状态矩阵Ac确定之后,对其进行特征值分解:
Ac=ψΛψ-1
(18)
式中Λ=diag(λk)∈Rn×n,k=1,2,…,n;λk为第k阶模态特征值;ψ为系统特征向量。
特征值与振荡频率和阻尼比存在下列关系:
(19)
式中:λk为系统第k个特征值;ωk为第k个振荡模式的振荡频率;ζk为第k个振荡模式的阻尼比。
进而求得系统第k个振荡模式的振荡频率及阻尼比[14]:
(20)
式中ak=Re(λk),bk=lm(λk)
系统的模态振型定义为输出点处的系统特征向量:
φ=Ccψ
(21)
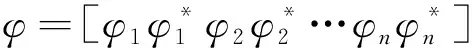
利用快速随机子空间算法辨识系统机电振荡模态参数,及时掌握系统当前的运行动态,对于调度运行人员进行准确有效的电力系统小干扰稳定分析具有重要意义。
3 仿真分析
3.1 4机2区域系统计算与分析
本节以IEEE 4机2区域系统为例,对提出的基于FSSI算法的电力系统模态参数快速识别方法进行仿真分析。IEEE 4机2区域系统结构如图1所示,数据参见文献[15]。

图1 4机2区域系统接线
利用小干扰稳定分析算法(Small Signal Analysis Stability, SSAT)计算系统基础运行方式下的机电振荡模式,分析结果如表1所示。三个机电振荡模式对应的模态振型如图2所示。
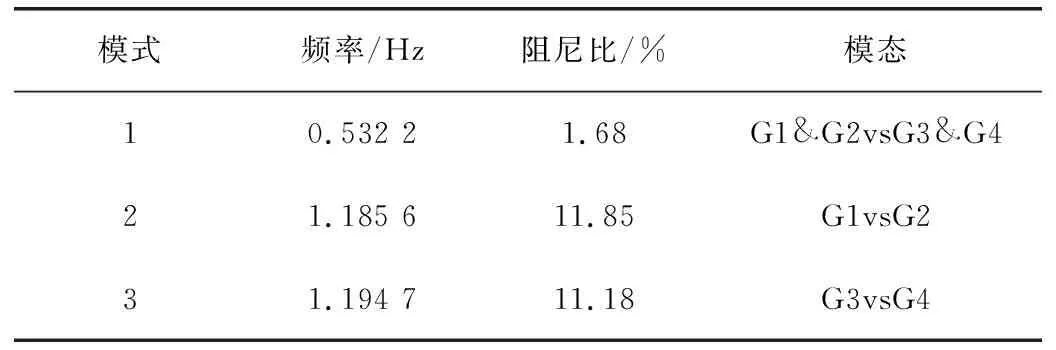
表1 4机2区域系统特征值分析结果
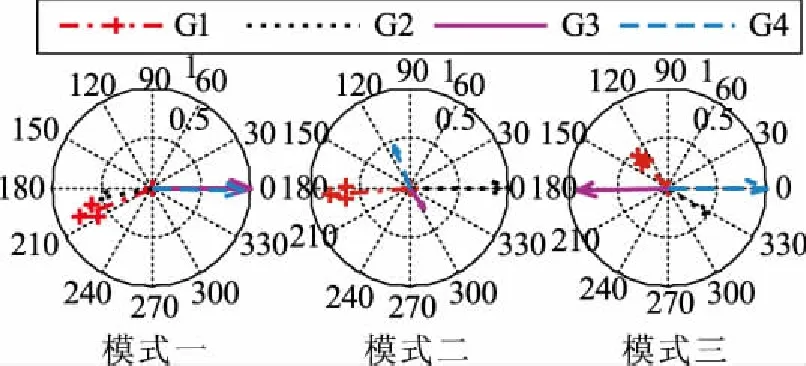
图2 4机2区域系统模态振型图
为了验证本文所提方法在电力系统模态参数识别方面的准确性和有效性,为模拟实际系统的负荷随机波动,本文假设节点4和节点14处的负荷以基础运行值的5%随机波动。
以系统各台发电机的角频率随机响应数据为基础,在惠普Z820(CPU:2*Intel至强E5-2600v3,2.6 GHz;内存:32 GB)工作站上分别利用传统随机子空间算法和本文提出的快速随机子空间算法,针对不同长度时间段的随机响应数据辨识系统模态参数。各长度数据段的CPU计算时间如表2所示。以120 s长度的发电机角频率随机响应数据段为例,分别利用传统SSI算法和本文提出的FSSI算法辨识系统模态机电振荡模态参数,分析结果如表3所示。
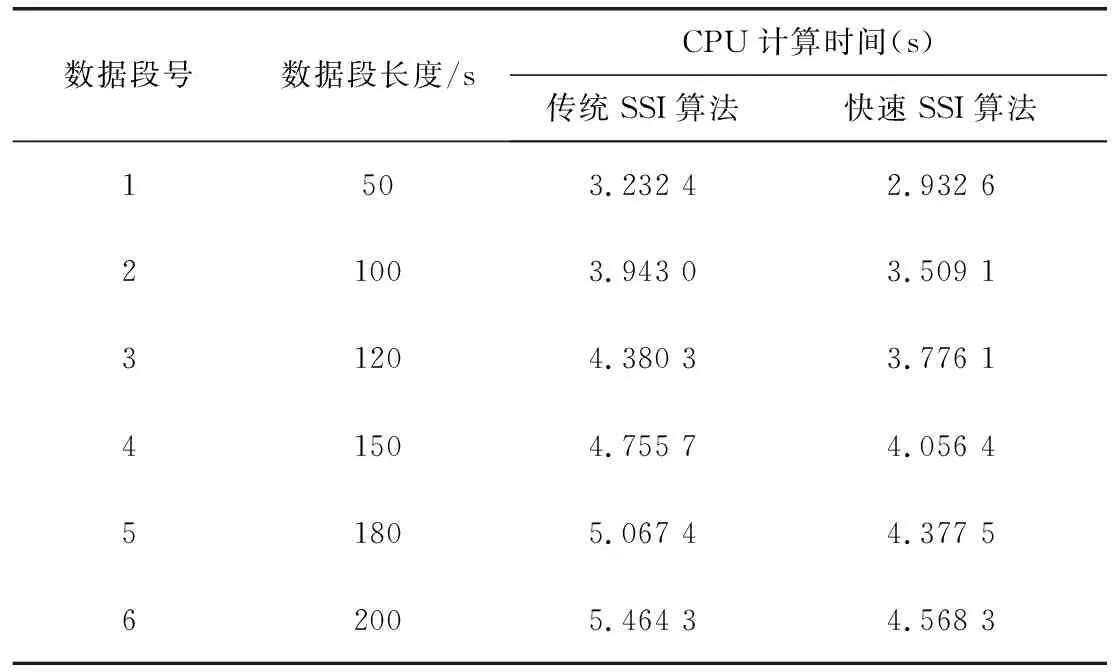
表2 4机2区域系统CPU计算时间

表3 4机2区域系统模态参数辨识结果
结合表2、表3及图3分析可知,利用本文提出的FSSI算法能够准确辨识出系统3个机电振荡模式,相对于传统SSI算法,辨识得到的三种模式振荡频率及阻尼比结果与基础运行方式的机电振荡参数更加接近;在计算速度方面,对于相同长度数据段,若数据较短,两种方法的计算时间相差不明显,但对于样本数据较多的情况,本文提出的方法具有较大的优势,CPU计算时间更少,具有更快的计算速率,能够更好的满足现代电力系统对安全稳定评估快速性的要求。
以系统角频率随机响应数据为基础,利用本文提出的快速随机子空间算法辨识得到系统振荡频率、阻尼比及模态振型信息。选取时长为20min随机响应数据为基础,以10s为数据窗口,每6s滑动一次计算窗口数据,20min内计算统计结果如表4所示,三个机电振荡模式的频率-阻尼比关系如图4所示。
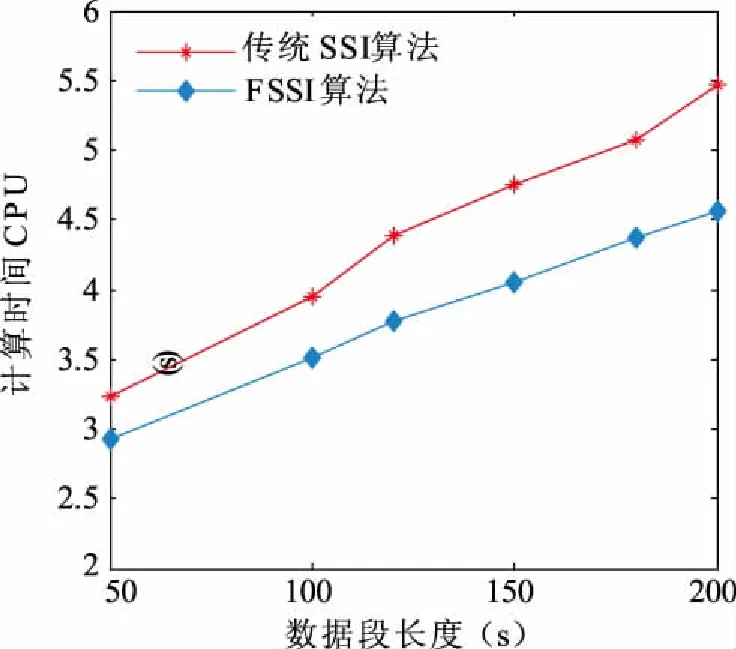
图3 4机2区域系统CPU计算时间变化图
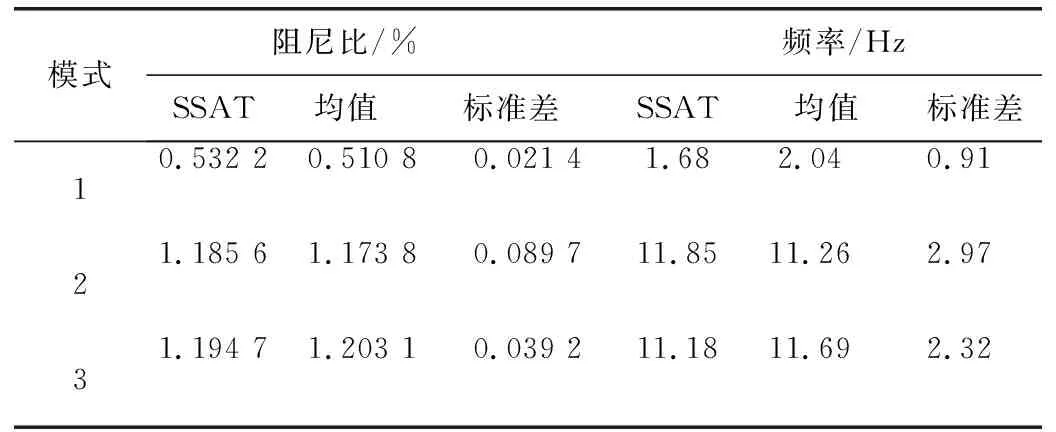
表4 机电振荡参数辨识结果
结合表1和表4分析可知,利用本文提出的FSSI算法辨识得到系统3个机电振荡模式的振荡频率分别为:0.520 8 Hz、1.173 8 Hz、0.532 2 Hz、1.203 1 Hz,基础运行方式下振荡频率分别为:0.532 2 Hz、1.185 6 Hz、1.194 7 Hz,统计均值与基础运行方式值十分接近,且标准差很小;同样,辨识得到的阻尼比分别为1.87%、11.26%、11.69%与基础运行方式值1.68%、11.85%、11.18%接近,标准差小。
快速随机子空间20 min内辨识得到的频率-阻尼比关系如图4所示。分析图4可知,系统各振荡模式每次滑动窗内辨识得到的频率和阻尼比均以基础运行值为中心分布,辨识得到的结果与基础运行值接近,辨识结果良好。
同时,图5所示的基于角频率随机响应数据辨识得到的模态振型反映的机组参与振荡的信息与图2所示的基础运行方式的模态振型形基本一致,进一步验证了本文提出的快速随机子空间方法的有效性。
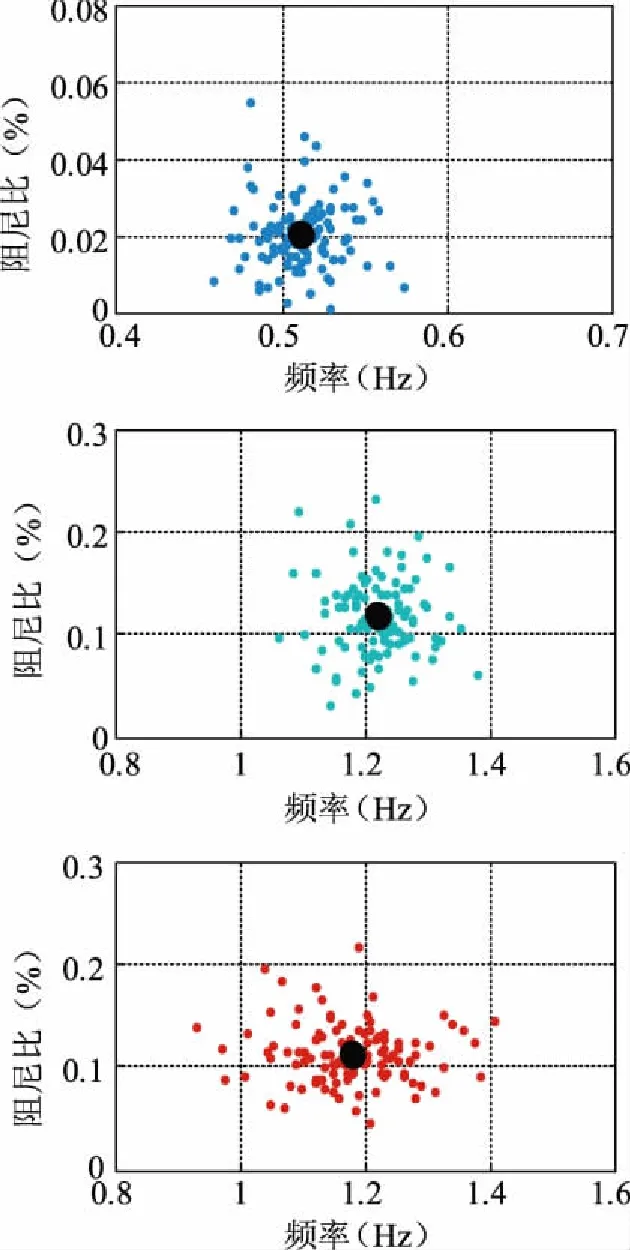
图4 4机2区域频率-阻尼比辨识结果
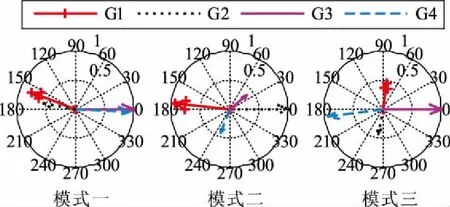
图5 4机2区域系统模态辨识结果
3.2 IEEE 16机68节点系统
IEEE 16机68节点系统结构图及数据参见文献[16]。
同样,对系统进行小干扰稳定分析,获取基础运行方式下系统机电振荡模式。就实际系统而言,区间振荡影响更为广泛,是调度运行人员主要关心的振荡模式。因此,本文主要针对16机68节点系统的区间振荡模式进行分析,得到系统4个区间振荡模式参数如表5所示,模态振型如图6所示。
与IEEE 4机2区域系统分析类似,假设系统内所有负荷均以基础运行值的5%随机波动,分别利用传统SSI算法和本文提出的FSSI算法,以角频率随机响应数据为基础辨识系统模态参数。不同长度数据段的CPU计算时间如表6所示。
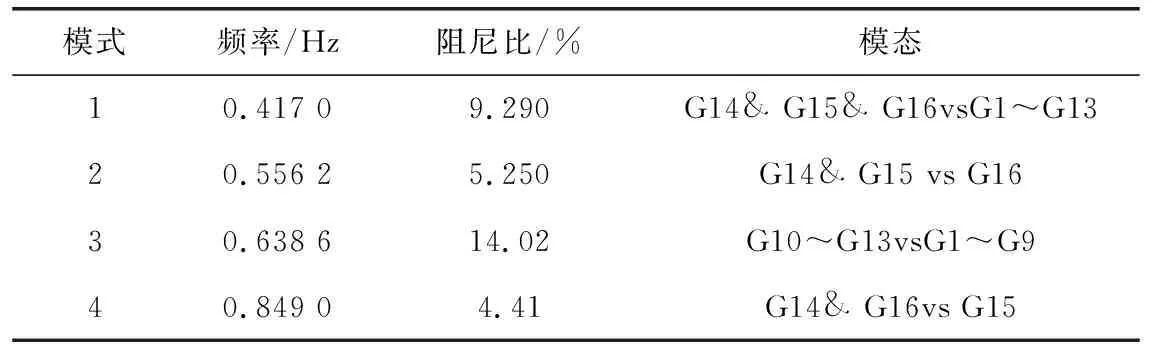
表5 16机68节点系统特征值分析结果
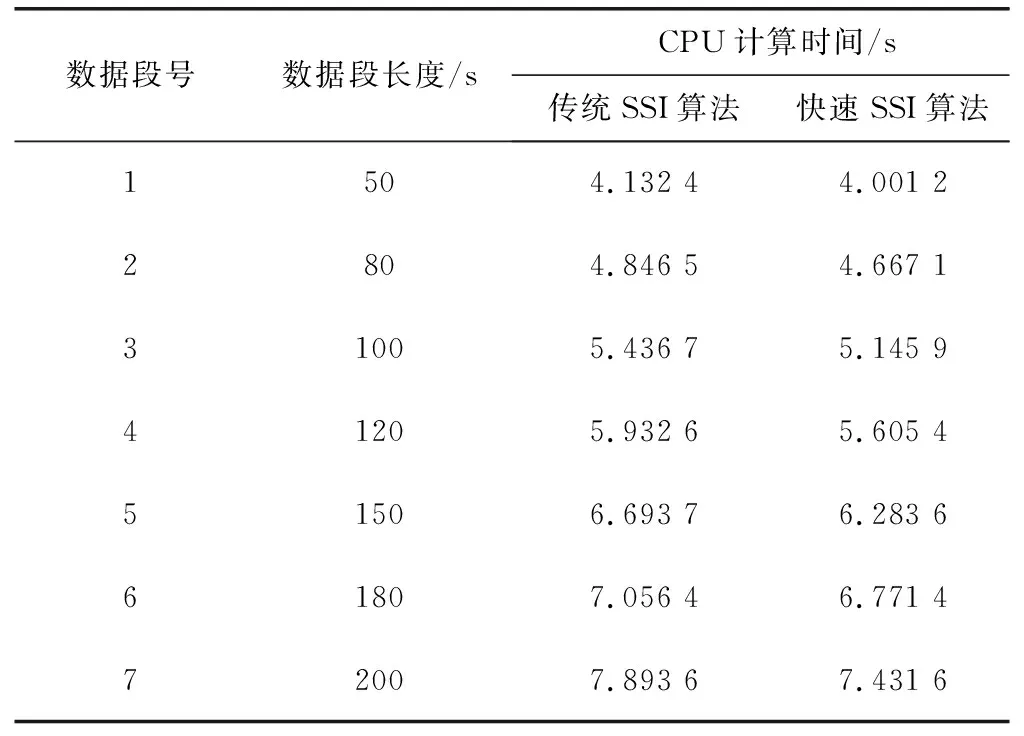
表6 16机68节点系统CPU计算时间
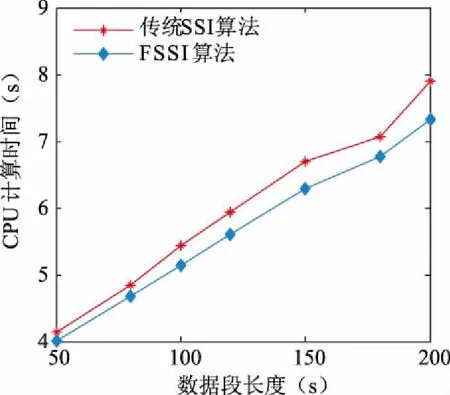
图7 16机68节点系统CPU计算时间变化图
结合表6和图7分析可知,由于16机68节点系统相对于4机2区域系统的系统规模大,两种辨识算法所需的时间均有所增加,但本文提出的快速随机子空间法相对于传统的随机子空间法的计算时间要少,计算速度快。
以20 min角频率随机响应数据为基础,10 s为数据窗口,6s滑动一次窗口数据,16机68节点系统20 min辨识得到的统计结果如表7所示,频率-阻尼比关系如图8所示。
分析表7可知,快速SSI辨识得到的4个区间振荡的振荡频率和阻尼比与基础运行方式下的模态参数十分接近,同时结合图8亦可以看出,每次滑动窗内辨识得到的频率和阻尼比以基础运行值为中心,在其周围分布,进一步验证了本文所提方法在系统模态参数辨识方面的有效性和准确性。
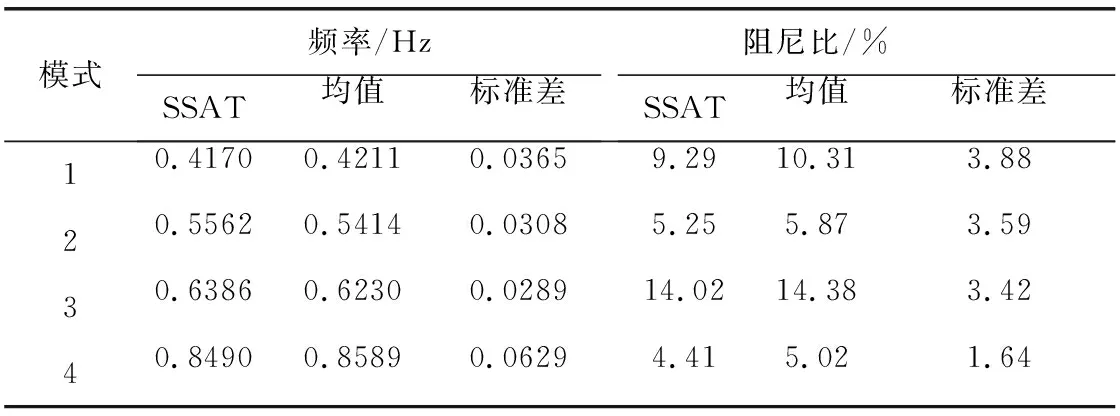
表7 16机68节点系统辨识结果统计
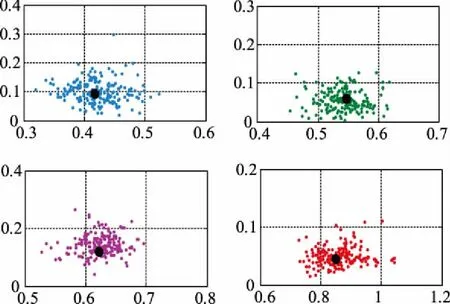
图8 16机68节点系统频率-阻尼比辨识结果
4 结束语
本文推导了环境激励下电力系统动态响应的解析表达式,利用快速随机子空间算法辨识系统振荡频率、阻尼比及模态振型,仿真分析与计算表明:
(1)环境激励作用下的系统随机响应蕴含丰富的动态信息,采用合适的参数识别技术能够从中提取出系统机电振荡参数;
(2)与传统随机子空间相比,本文提出的快速随机子空间算法以LQ分解法为基础,降低了CPU计算时间,有效提高了辨识速度,更好的满足了电力系统安全稳定评估快速性的要求;
(3)快速辨识系统机电振荡参数,及时掌握系统动态信息,为调度运行人员采取及时有效的控制措施提供依据。
电力系统模态参数识别的结果是为了更好的实现电力系统小干扰稳定分析控制,如何根据辨识结果采取有针对性的控制措施是下一步需要考虑的问题。
