中考微专题教学:由浅及深与同类跟进
——以抛物线“内接三角形”问题为例
2018-10-25江苏省海安市海陵中学李海凤
☉江苏省海安市海陵中学 李海凤
二次函数的图像是抛物线,各地中考以抛物线为背景,结合其“内接三角形”进行探究的习题丰富多彩,本文关注抛物线结合其“内接特殊三角形”与一元二次方程之间的对应关系(即“形数对应”),为了便于教学研究,我们以习题教学的形式构思了一节中考微专题教学课例,现梳理出来,分享给大家.
一、抛物线“内接三角形”习题课例概述
例1如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点.
(2)当△ABC是直角三角形时,求证:ac=-1.
教学预设:(1)令y=0,则关于x的一元二次方程ax2+bx+c=0的两根)对应着B、A两点的横坐标.于是
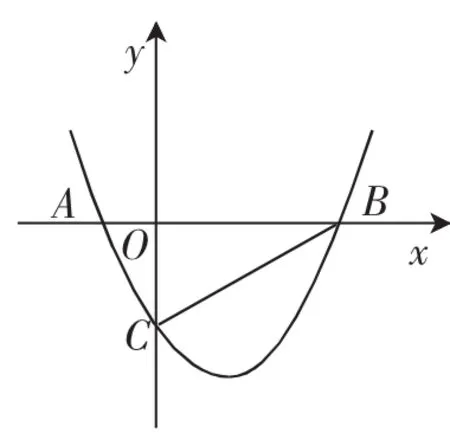
图1
(2)由△ABC是直角三角形,可证△AOC △COB,把对应边的比例式转化为乘积式,得OC2=OA·OB.接下来“从形到数”,把它们对应的“坐标”代入乘积式,得c2=,化简可得ac=-1.
教学时注意引导学生体会数形对应、数形互助的数学思想方法.可以使用如下的板书设计帮助学生理解这里的数形对应.
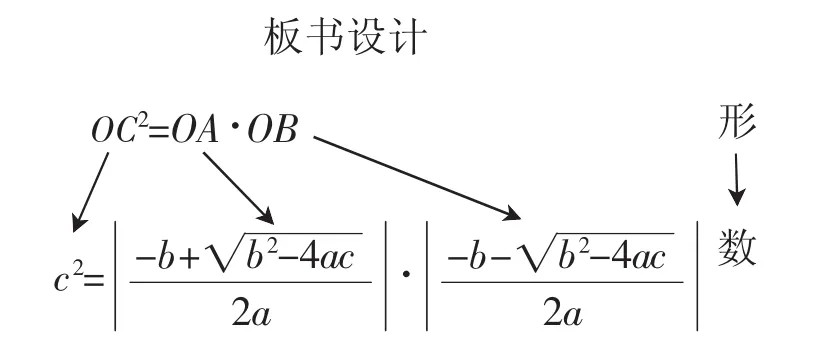
跟进练习:已知二次函数y=3x2+bx+c的图像与坐标轴分别交于A、B、C三点,若△ABC是直角三角形,则c的值为______.
解题预设:根据例1(2)中的结论“当△ABC是直角三角形时,ac=-1”,可直接写出3c=-1,解得c=-.
例2平面直角坐标系xOy中,顶点为C的抛物线y=ax2+bx+c与x轴交于A、B两点.
(1)若△ABC为直角三角形,求证:b2-4ac=4;
(2)若△ABC为等边三角形,求证:b2-4ac=12;
(3)若△ABC中∠ACB=120°,求证:b2-4ac=.
教学预设:根据题干信息,有如下一些准备工作.画出图2进行分析(设a>0,抛物线开口向上),结合抛物线的对称性质可确认△ABC一定是等腰三角形,且CA=CB.接着抛物线y=ax2+bx+c与x轴(即直线y=0)交于A、B两点.则点A、B的横坐标对应着关于x的一元二次方程ax2+bx+c=0的两根,可算出AB的长为.表示出抛物线的顶点C的坐标作CH⊥AB交x轴于H,则等腰三角形ABC底边上的高CH就是
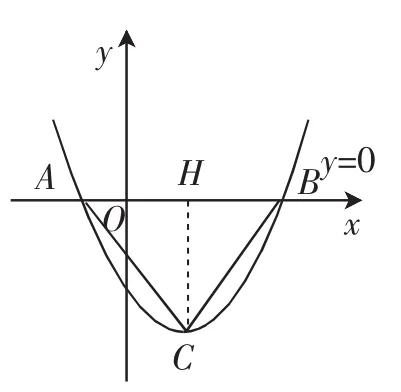
图2
(1)若△ABC为直角三角形,则△ABC为等腰直角三角形,则AB=2CH,则,变形得b2-4ac=4.
讲评提醒:贯通思路之后,可以与例1中提醒学生数形对应的板书一样,给出相应的板书(略).
拓展预设:因为x轴就是直线y=0,还可将x轴一般化为直线y=n,有如下更一般的情形与性质.
走向一般:如图3,平面直角坐标系xOy中,顶点为C的抛物线y=ax2+bx+c与直线y=n交于A、B两点.抛物线y=ax2+bx+c与直线y=n联立得到关于x的一元二次方程ax2+bx+c-n=0.若△ABC为直角三角形,是否有b2-4a(c-n)=4?
简证:关于x的一元二次方程ax2+bx+c-n=0的两根为,可算出AB的长为.表示出抛物线的顶点C的坐标),如图3,作CH⊥AB交直线AB于H,则等腰三角形ABC底边上的高CH就是


图3
若△ABC为直角三角形,则△ABC为等腰直角三角形,则AB=2CH,则,变形得b2-4a(c-n)=4,仍然满足一元二次方程ax2+bx+c-n=0的Δ=4.
类似的,仍然可证得:若△ABC为等边三角形,有b2-4a(c-n)=12;若△ABC中∠ACB=120°,有b2-4a(cn)=.
跟进练习:(1)二次函数y=ax2+bx+c的图像与x轴有两个交点A和B,顶点为C,且b2-4ac=4,则∠ACB的度数为( ).
A.30° B.45° C.60° D.90°
(2)二次函数y=ax2+bx+1(a≠0)的图像与x轴有两个交点A、B,顶点为C.若△ABC恰好是等边三角形,求代数式b2-2(2a-3)的值.
预设解答:根据例2,对于(1),可直接看出∠ACB为90°;对于第(2)问,稍加包装,把代数式b2-2(2a-3)展开整理得b2-4a+6,再对照二次函数表达式中常数项c=1,将待求式子转化为b2-4ac+6,结合△ABC恰好是等边三角形,可得b2-4ac=12,于是代数式b2-2(2a-3)的值为18.
二、教学思考
1.加强同类收集,是数学解题研究的一种追求
教师的解题研究不能满足于解一题丢一题,而要注意收集、关联同类习题,并及时整理存档,重视个人教学素材库的建设.笔者的一般做法是,在电脑上有相应的文件夹,想好同类题的主题命名文件夹,比如,本文关注的主题可命名为“主题关注 抛物线与内接三角形 形数对应”,这样日后检索资料时可以根据不同的关键词很快查找到,而且后续有类似的素材更新时,也可继续添加到相应主题的文件夹中.
2.重视解后回顾,让解题研题服务于习题教学
解后回顾对于师生的解题都是十分必要的,是加深理解、增强记忆的好方法.特别是教师解后回顾,不但要想清问题的结构与本质,还可从服务习题教学的角度进行思考,问题还有哪些可能的变式?已有性质的发现能否进行推广?上文例2的教学拓展,就是这方面的一个重要应用.习题课教学中,注重变式,善于引导学生“走向一般”思考问题的习惯,不但对一道习题的理解更加深刻,达到解一题、会一类的效果,更重要的是向学生传递了数学的特点,比如数学的抽象思想、一般化及模型思考.
3.构思板书设计,使习题教学难点得到化解
习题课教学也需要经营板书,而不是杂乱无章的解题步骤,而且除了解题步骤的构思、排版,对于关键步骤、重要的转化策略、解题难点,还需要有另外的板书构思,这也是教学艺术的体现.在上文例1、例2思路讲解之后,我们分别给出两处体现“形数对应”的板书设计,通过不同标注、箭头示意等形象的方式呈现出来,根据教学观察,多数学生在记录课堂笔记时,对老师这种精心设计、形象的板书细节,都能“完好”地记录在他们的听课笔记上,也对他们理解难点起到很好的帮助作用.
