常教常新,不思何来
——苏科版七年级下“9.4乘法公式(2)”反思
2018-10-25江苏省南京市玄武区十三中锁金分校王建莉
☉江苏省南京市玄武区十三中锁金分校 王建莉
叶澜教授说:“一个教师写一辈子教案不一定成为名师,如果一个教师写三年反思,有可能成为名师.”我最近上了一堂苏科版七年级下“9.4乘法公式(2)”新授课,从问题情境、例题教学等方面感觉有些遗憾,现简要再现,并加以评析,就教于行家.
一、内容和内容解析
内容:平方差公式.
内容解析:为了进一步理解平方差公式,可以利用(a+b)(a-b)=a2-b2的几何意义——面积,运用表示面积的方法解释平方差公式,以便直观地把握公式,体会数形结合思想.基于以上分析,确定本节课的教学重点:平方差公式.
二、案例描述
1.问题情境
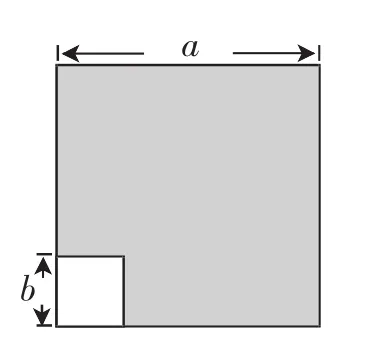
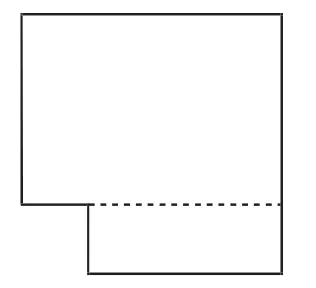
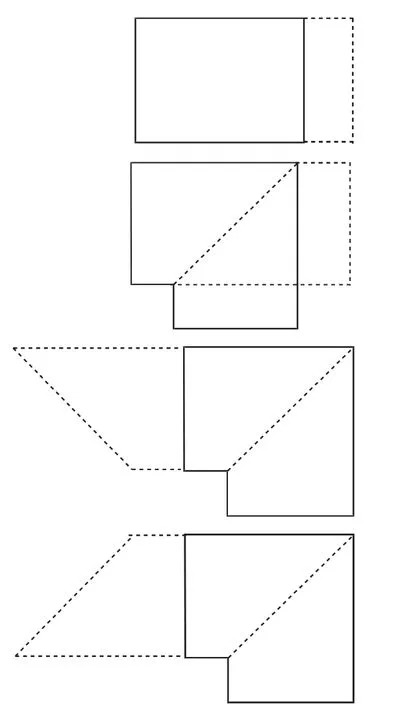
问题呈现(数学实验室):在边长为a的正方形纸上剪去一个边长为b(b 师:同学们观察一下这个图形,该如何求阴影部分的面积? 给学生充分的思考时间. 生1:用大正方形的面积减去小正方形的面积,即a2-b2. 师:好的,有没有其他方法? 图1 生2:因为阴影部分是不规则图形,所以求它的面积可以用“割补法”来求. 师:你准备用“割”还是“补”的方法? 生2:用“割”的方法. 师:你能画出图形,并把你的求解过程写在黑板上吗? 生2板演:如图2,阴影部分的面积是:a(a-b)+b(a-b)=a2-ab+ab-b2=a2-b2. 生3:还可以割成梯形. 师:你能画出图形,并把求解过程写在黑板上吗? 图2 图3 生4:老师,割完后还可以拼起来,如图4,阴影部分的面积就是(a+b)(a-b). 此时,学生情绪高涨:哦,原来还可以割完后把图形再拼起来. 图4 师:因为不论用什么方法,我们求的都是阴影部分的面积,所以求出的结果是相等的,由此我们得到了另一个乘法公式(a+b)(ab)=a2-b2,我们把这个公式叫作平方差公式,你能用文字语言描述一下这个公式吗? 生5:两个数的和乘以这两个数的差,等于它们的平方差. 教师板演例1: 例1 (1)(5x+y)(5x-y);(2)(m+2n)(2n-m);(3)(3y-x)(-x-3y). 师:这三题在形式上符合今天的平方差公式的特点吗?如果符合,你能找到a和b吗? 生5:第(1)题中,a=5x,b=y,符合平方差公式的特点. 生6:第(2)题中,a=2n,b=m,符合平方差公式的特点. 生7:利用加法交换律把第(3)题变形成(-x+3y)(-x-3y),所以a=-x,b=3y. 师生共同总结:(1)公式中的a、b可以表示任意式子(包括单项式、多项式或其他代数式);(2)用平方差公式时注意一定要找到a和b,与a和b的顺序无关. 苏科版教材第78页练一练1、2、3. 问题情境设计的目的是让学生通过操作,用不同的方法计算面积,感受探讨整式乘法的运算方法.在利用面积法推导平方差公式时再次让学生感受面对不规则图形求面积的方法,就是转化成规则图形,可以“补”,也可以“割”.在八年级上学期我们还将用这种方法推导出勾股定理.《义务教育数学课程标准(2011年版)》要求学生能利用公式进行简单的计算,学生的参与度是很高的.但是在问题情境设置上还是存在着缺憾. 缺憾1:推导乘法公式不够严谨. 利用面积法推导乘法公式,那么字母的范围是正数,而平方差公式的适用范围是任意实数,所以单纯利用面积法推导是有局限性的. 缺憾2:将一个正方形减去另一个正方形这个背景突然给学生,感觉有点突兀,应给学生一点思考空间,使他们自己能够想到怎样构造图形. 建议1:问题情境改为: 计算下列多项式的积,你能发现什么规律? (1)(x+1)(x-1)=_____;(2)(m+2)(m-2)=_____;(3)(3x+1)(3x-1)=_____. 学生猜想并验证得到公式(a+b)(a-b)=a2-b2. 师:你能利用图形验证它吗? 设计意图:利用几个具体实例让学生体会乘法公式和多项式乘多项式的关系,再追问可否用图形验证这个公式,因为我们前面已经有利用图形验证完全平方公式的经验了,那么思考这个问题便水到渠成了,可让学生体会数形结合的思想. 缺憾3:例题设置可以变化再多一点,本节课除了重点是公式的推导,还有个重点、难点是平方差公式的运用,要求能灵活利用平方差公式进行简单计算,所以除了把a换成单项式,还可以换成多项式,a和b的顺序可以再变化一下,还有每一项符号的变化. 建议2:例题可以这么改: (1)(5x+y)(5x-y);(2)(y+5x)(5x-y);(3)(y+5x)(-y+5x);(4)(-5x+y)(-5x-y);(5)(y-5x)(-5x-y);(6)(y-5x)(5x-y). 设计意图:其中第(6)题不符合平方差公式,可以让学生做个辨析,说一说为什么不符合平方差公式的特点(平方差公式两个小括号中必须要有一项符号相同).学完平方差公式后,学生们很容易分不清完全平方公式和平方差公式. 在做第(5)题时也有不同的处理方式: 法一 :(y-5x)(-5x-y)=(-5x+y)(-5x-y)=(-5x)2-y2=25x2-y2. 法二:(y-5x)(-5x-y)=(5x-y)(5x+y)=25x2-y2. 符号变化可能是在每一项上,还可能放在括号外,例如: 拓展:(7)(x+y+z)(x+y-z);(8)(x+y-z)(x-y+z). 对于(7),(x+y+z)(x+y-z)=[(x+y)+z][(x+y)-z]=(x+y)2-z2.把两个小括号内符号相同的项组合在一起作为a. 对于(8),(x+y-z)(x-y+z)=[x+(y-z)][x-(y-z)]=x2-(y-z)2.把两个小括号内符号不相同的项组合在一起作为a. 课堂是开放的,教学是生成的.乘法公式的教学本身比较枯燥,问题情境及例题如果这样设置,既能调适课堂教学氛围,又激发了学生学习研究的兴趣. 整式乘法: 教师应顺应学生的思维习惯、思维方向,合理、有效地整合教材,设计教案,充分激发学生学习探究的兴趣,使其由“要我学”主动转入“我要学”,有的放矢地引导学生成功步入“最近发展区”,感觉数学不是那么难,根据数据、图形的特征找到线索,进行合情推理. 真正理解公式,就是抓住公式的本质.公式本身看上去不难,但是在顺序、符号及项数上稍加改变,学生就不认识了,所以在例题设置上,可以将一题稍加变化,渗透数学思想方法,让学生从形上辨析. 带着我们的学生再次反思一下作业中的题目的解法,所有题目都可以用通法解决,但是有些题目在结构上有其自己的特色,导致有其独特的简单解决方法,要把对题目的理解与学生分享: 例如,(-2y2-3x)(3x-2y2). 通法:原式=(-2y2-3x)(-2y2+3x)=4y4-9x2. 特法:原式=(2y2+3x)(2y2-3x)=4y4-9x2. “吾日三省吾身”,说的就是“反思”,教学反思恰如一位向导,带领我们从经验迷宫走向智慧殿堂.F2.建构活动

3.数学认识
4.建构活动
5.基础训练
三、案例反思
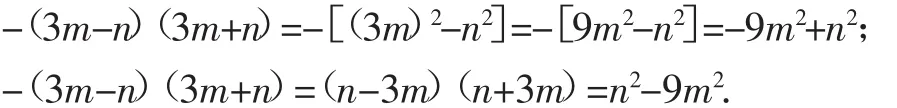

四、启示
1.吃透教材,改组教材,拓展教材
2.抓住公式、概念的本质,努力提高教师的应变能力及学生举一反三的能力
3.作为教师,不仅要反思教学设计、教学方法,还要反思例题、习题的解题方法
