辅助圆的构造策略与解题技巧
2018-10-25钟珍玖
钟珍玖
圆是初中最为重要的基本图形之一,圆中的弧、弦、圆心角、圆周角有很多常用的性质,是解决圆中有关计算和推理的基础,所以构造辅助圆,运用圆的有关性质解决问题是学习圆的重点和难点.下文对构造辅助圆的方法和解题的技巧进行归纳.
一、运用圆的定义构造辅助圆
教材上关于圆的定义有两种.一种是从运动的角度定义圆:把线段OP绕点O旋转一周,点P运动所形成的图形;另一种是集合定义:圆是到定点的距离等于定长的点的集合.根据圆的集合定义,当问题中有若干个点到某一点距离相等时,可以考虑构造辅助圆解决问题.
例1(1)如图1,将△ABC绕着A点逆时针方向旋转一定的角度后得△ADE,连接BD、CE,则△ABD与△ACE相似吗?请证明你的结论.
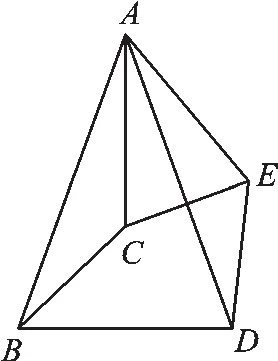
图1
(2)如图2,在矩形ABCD中,AB=3,AD=5,将矩形ABCD绕点A逆时针方向旋转一定的角度后得到矩形AEFG,使矩形AEFG的边EF恰好经过点D,连接BE,则BE的长为______.

图2
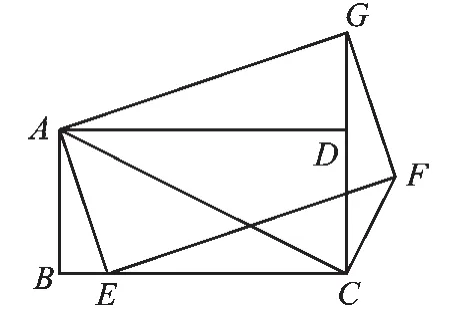
图3
【解析】解:(1)△ABD与△ACE相似.由旋转得:△ABC≌△ADE,
∠BAD=∠CAE,
∴AB=AD,AC=AE,

∴△ABD∽△ACE.

图4
(2)如图4,连接GD.∵∠BAE=∠DAG,BA=EA,GA=DA,

又∵在Rt△AED中,
AE=3,AD=5,
∴ED=4,∴DF=1,
∴在Rt△GFD中,


(3)点E在边BC上的运动过程中,∠ACF的大小总保持不变.
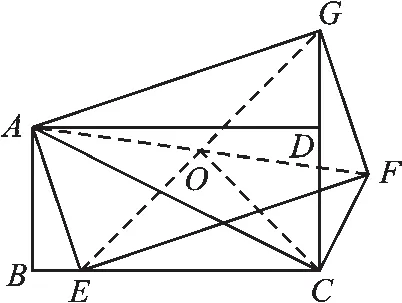
图5
∵四边形AEFG是矩形,
∴OA=OF,OE=OG,AF=EG,
∴OA=OF=OE=OG,
∵四边形ABCD是矩形,
∴∠ECG=90°,
∴OC=OE,
∴OA=OF=OE=OG=OC,
∴点C、E、F、G、A在以O为圆心的圆上,
∴AF为圆O的直径,
∴∠ACF=90°,
即∠ACF的大小保持不变.
【点评】本题的第三题可以用第一题的思路,证明△ABE∽△ACF,运用相似三角形的对应角得到∠ACF为定角90°,对推理能力要求较高.由到定点的距离等于定长构造辅助圆,运用圆的性质“直径所对的圆周角为90°”解决问题,简洁明了,体现了思维的灵活性.
例2 如图6,在△ABC中,AB=AC=5,

图6
(1)如图7,当点B1在线段BA的延长线上时,求证:BB1‖CA1.

图7
(2)如图8,E是BC的中点,F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F对应的点为F1,求线段EF1的长度的最大值与最小值的差.

图8
【解析】解:(1)由旋转得BC=B1C,∠ACB=∠A1CB1,
∴∠B=∠BB1C,
∵AB=AC
∴∠B=∠ACB,
∴∠A1CB1=∠BB1C,
∴BB1‖CA1.
(2)如图9,连接AE,作CF⊥AB于点F.以点C为圆心,CF为半径画圆交BC于点F2,此时EF1最小,即为EF2;以点C为圆心,BC为半径画圆交BC的延长线于F3,此时EF1最大,即为EF3.

图9
∵AB=AC,E为BC的中点,
∴BE=CE=AB·cos∠ABC=3,
∴AE=4,
∵BC·AE=AB·CF,
∴CF=4.8,
∴EF2=CF2-CE=4.8-3=1.8,
EF3=CF3+CE=6+3=9,
∵EF3-EF2=7.2,
故线段EF1长度最大值与最小值的差为7.2.
【点评】在很多的动态问题中,特别是翻折和旋转的图形运动中,都存在到定点的距离等于定长的情形.构造辅助圆是解决这类问题的有效方法,解题的策略仍然是运用圆的性质.
本题利用了圆外或圆内的点与圆心的连线跟圆相交,所得线段有最大值和最小值的结论.这也是圆中求单线段最值的常用方法.
二、运用定线段对定角构造辅助圆
在很多问题中,如果一条定线段的张角是定值,那么这个角的顶点在以定线段为直径或者为弦的圆上,此时构造辅助圆解题较为方便.
例3已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0),A(5,0),B(m,2),C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
【分析】(1)如图10,由四边形四个点的坐标易得OA=BC=5,BC‖OA,构造以OA为直径的⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°.作DG⊥EF于G,连接DE,则DE=OD=2.5,DG=2.根据垂径定理得 EG=GF.接着利用勾股定理可计算出EG=1.5,于是得到E(1,2),F(4,2),即点P在E点和F点时,满足条件.此时,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°.
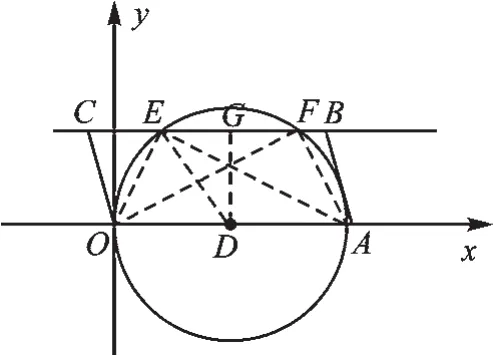
图10
(2)如图11,先判断四边形OABC是平行四边形,由题意易得∠AQO=90°.以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,于是得到点Q只能是点E或点F.当Q在F点时,证明F是BC的中点,而F点为(4,2),得到m的值为6.5;当Q在E点时,同理可求得m的值为3.5.
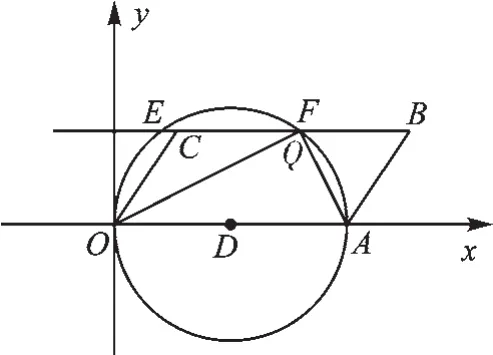
图11
解:(1)存在.
∵有O(0,0)、A(5,0)、B(m,2)、C(m-5,2),
∴OA=BC=5,BC‖OA,
以OA为直径作⊙D,与直线BC分别交于点E、F,
则∠OEA=∠OFA=90°,
如图10,作DG⊥EF于G,连接DE,则DE=OD=2.5,DG=2,EG=GF,

∴E(1,2),F(4,2),
∴点P在E点和F点时,有∠OPA=90°,
(2)如图11,
∵BC=OA=5,BC‖OA,
∴四边形OABC是平行四边形,
∴OC‖AB,
∴∠AOC+∠OAB=180°,
∵OQ平分∠AOC,AQ平分∠OAB,

∴∠AOQ+∠OAQ=90°,
∴∠AQO=90°,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,
∴点Q只能是点E或点F.
当Q在F点时,
∵OF、AF分别是∠AOC与∠OAB的平分线,BC‖OA,
∴∠CFO=∠FOA=∠FOC ,∠BFA=∠FAO=∠FAB,
∴CF=OC,BF=AB,而OC=AB,
∴CF=BF,即F是BC的中点.
∵F点为(4,2),
∴此时m的值为6.5.
当Q在E点时,同理可得m的值为3.5,
∴综上所述,m=3.5,6.5.
【点评】这是一道有一定难度的综合题.引入辅助圆以后,运用圆的性质解题,问题就得到简化.所以构造辅助圆解题可以简化运算,优化方法.
辅助圆通常是隐含在题目中的,所以很多老师也称之为“隐圆”,其构造的策略就是运用圆的集合定义和定弦对定角,解题的方法就是运用圆丰富的性质.

