圆有关概念的错题剖析

杭 蕙

“对称图形——圆”这一章概念比较多，概念的运用也比较广泛，如果对概念分辨不清，理解不透，掌握不扎实，解决问题的过程中就会混淆，产生一些不该出现的简单错误.现举出常见的几例进行剖析，希望同学们能引以为鉴.

一、垂径定理

例1如图1，⊙O的弦AB垂直平分半径OC，且OC=4，则AB=

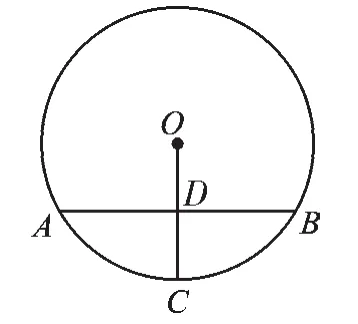
图1

【错解】

【错解剖析】本题已知半径的长度以及弦垂直平分半径，从而可以把半径、弦心距、弦长的一半“集中”在同一个直角三角形中，利用勾股定理计算出弦长的一半，即.有的同学往往把这个答案当成最终答案，这是解题不够细心导致的错误.当求得时，这只是弦长的一半，应再利用垂径定理得出整条弦AB的长度.AB长为.

【正解】如图2，连接OA（当然也可连接OB），得出直角三角形OAD，因为OA=4，OD=2，由勾股定理可得AD=再利用垂径定理即可求出弦AB的长度是

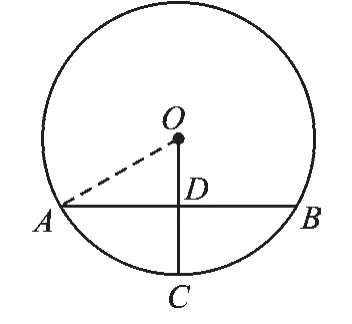
图2

二、切线性质

例2如图3，AB与⊙O相切于点B，AO的延长线交⊙O 于点 C，若∠A=50°，则∠C=______.

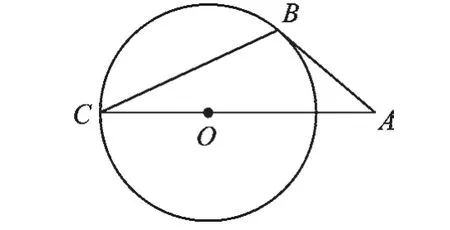
图3

【错解】40°.

【错解剖析】本题已知条件中有直线与圆相切，同学们很容易想到切线及其性质，但有些同学对于“圆的切线垂直于经过切点的半径”这一概念没有真正掌握，在解题时，就直接把∠ABC当作90°，从而得出错误答案∠C=40°.对于本题，如果理解了概念中“经过切点的半径”这一关键点，就会自然地想到用“见切点，连半径”来解决了.

【正解】连接OB，如图4，

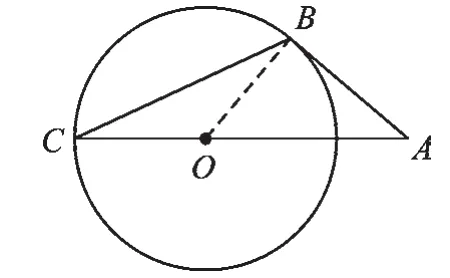
图4

可得∠OBA=90°.

∵∠A=50°，

∴∠BOA=40°，

又∵OB=OC，

∴∠C=20°.

三、圆周角

例3如图5，A，B，C是⊙O上的三点，∠ACB=20°，∠OAC=30°，求∠OBC的度数.

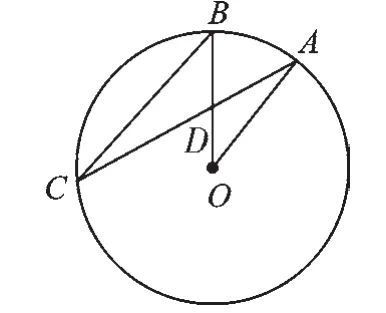
图5

【错解】30°.

【错解剖析】本题结论要求出一个角的度数，并把这一问题放在了圆这个背景中.结合已知条件，同学们会联想到用圆周角、圆心角的知识来解决问题.但有些同学对同弧所对的圆周角概念不清楚，在解题时，错把∠OAC和∠OBC当作是同弧所对的圆周角，从而得出了错误答案.

仔细审题，不难发现本题应利用同弧所对的圆心角和圆周角的关系及三角形内角和为180°（或三角形外角性质）来求解.

【正解】因为∠AOB和∠ACB是同一弧⁀所对的圆心角和圆周角，

∴∠AOB=2∠ACB=40°，

∴∠AOB+∠OAC=40°+30°=70°，

∴∠ADO=∠BDC=180°-70°，

∴∠BCA+∠CBO=70°，

这样就容易求得∠OBC=50°.

四、圆和直线的位置

例4已知⊙O的半径为5，点P到圆心O的距离为5，则过点P的直线MN与⊙O的位置关系是_______.

【错解】相切.

【错解剖析】本题没有给出图形，同学们既不能直观地理解，又可能因分不清楚“点到直线的距离”和“点到点的距离”的区别，误把这两种情况当成是同一种情况，从而导致答案不完整，只答对了一种位置关系.

对于没有给出图形的题目，同学们应该做到“心中有图”，自己画出图形帮助理解，有了图形，便可以帮助自己分析问题、理解问题的本质，提高解题的正确率.实际上“点到点的距离”就是两点之间的线段长度，而“点到直线的距离”是指“点到直线的垂线段的长度”.同学们真正理解这两者的区别，再结合图形，很容易就能得出正确答案.

【正解】相切或相交.