数形结合 “圆”满解决

陈秋晓

在直线与圆的位置关系中，切线是特殊的情况，也是“圆”这一章所研究的重要内容.但是切线的性质与判定又是同学们容易弄错的地方.在历届中考中，都不乏有关圆的切线的证明与计算等问题，而在这类问题中，常常隐藏着一些不确定的因素.如果我们在解题中，能够数形结合，全面了解，就可以避免漏解，“圆满”解决问题.

类型一：由数到形，判断直线与圆的位置关系

例1已知⊙O的半径为3，直线l上有一点P，且PO=3，则直线l与⊙O的位置关系是（ ）.

A.相切 B.相离

C.相离或相切 D.相切或相交

【错解】A.

【错解原因】通过圆心到直线距离d与圆半径r的大小关系，可以判定直线与圆的位置关系.同学们在没有具体图形的情况下，会误以为d=r，从而判断直线l与⊙O相切.事实上，圆上所有点到圆心的距离都等于半径，过圆上的点既可以作圆的切线，也可以作与圆相交的直线，题目中并没有明确直线l与线段OP互相垂直，因此应分类讨论.如果同学们画画图，就不难发现，直线l与⊙O的位置关系需要分类讨论了.

【正解】D.

解：如图1，应分两种情况.

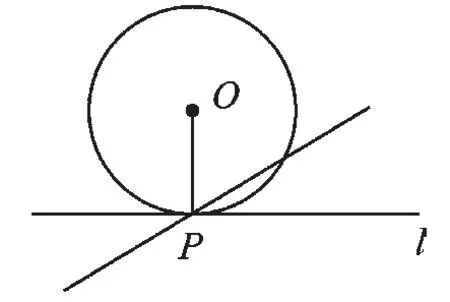
图1

①当直线l与OP互相垂直时，圆心O到直线l的距离d=OP=3=r，此时⊙O与直线l相切；

②当直线l与OP不垂直时，圆心O到直线l的距离d＜3=r，此时⊙O与直线l相交.

类型二：由形到数，确定数值

例2 如图2，射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC‖QN，AM=MB=2cm，QM=4cm.动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值________（单位：秒）

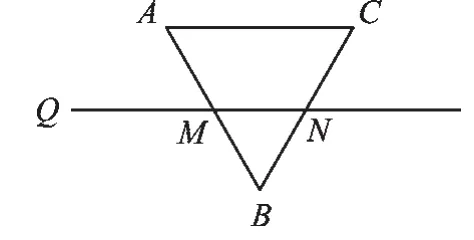
图2

【错解】t=2、t=4、t=6或t=8.

【错解原因】圆的切线垂直于经过切点的半径.同学们在分类讨论的时候，不难发现⊙P分别在边AB，BC的左侧与右侧时，与AB边，BC边相切的四种情形，较易求得四解.但极易忽略与AC边相切的情形，其实，从⊙P与边AC相切于点A开始，向右运动到相切于点C结束，整个运动过程都满足要求.

【正解】t=2或3≤t≤7或t=8.

解：分为3种情况.

①如图3，当⊙P切AB于点D时，∠PDM=90°.

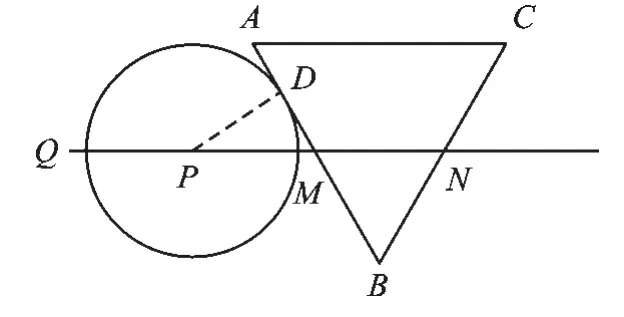
图3

∵∠PMD=∠BMN=60°，

∴∠DPM=30°.

∴DM=1cm，PM=2MD=2cm，

故QP=QM-PM=4cm-2cm=2cm.

∴t=2.

②如图4，当⊙P切AC于点A时，连接PA.

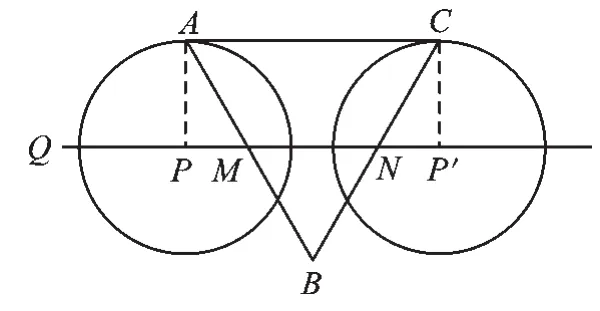
图4

同①可得PM=1cm，

∴QP=QM-PM=4-1=3cm，

故t=3；

当⊙P切AC于点C时，设P位于P′处，连接P′C.

易得QP′=QM+MN+NP′=4+2+1=7cm，

故t=7.

∵从⊙P与边AC相切于点A开始，到⊙P与AC相切于点C结束，整个向右运动过程中，⊙P一直与AC相切.

∴3≤t≤7.

③如图5，当⊙P切BC于点E时，

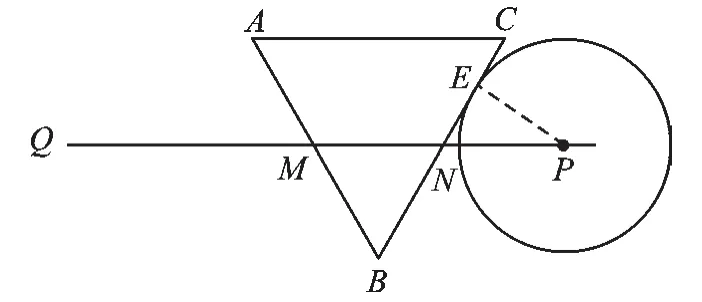
图5

∴NP=2.

∴QP=QM+MN+NP=4+2+2=8cm，

∴t=8.

注意：当⊙P运动到AB右侧与AB相切，以及运动到BC左侧与BC相切时，这两个时间都在第②种情况的运动时间内.如图6，图7所示.

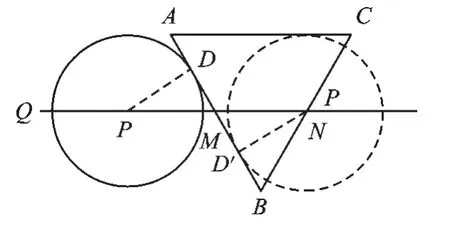
图6

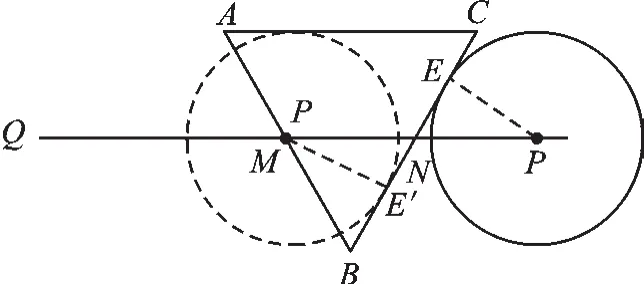
图7

综上所述：t=2或3≤t≤7或t=8.