低轨LTE卫星随机接入前导设计及检测算法研究
2018-10-24睿1
丁 睿1,刘 召,甄 立,秦 浩
(1.中国空间技术研究院,北京100094;2.西安电子科技大学 通信工程学院,西安710071)
1 引 言
卫星移动通信系统具有通信频带宽、通信容量大、覆盖面广、业务丰富、机动灵活、不受地理条件限制等特点,并凭借在应急救灾、互联网应用、医疗卫生、公共教育、民用业务通信、交通运输等领域的独特优势,成为国内外各界研究和竞争的焦点[1-2]。伴随着长期演进(Long Term Evolution,LTE)技术的成熟发展,以LTE技术为体制的卫星移动通信系统也成为了移动通信领域的研究热点[3]。根据卫星移动通信特性,将LTE技术应用于卫星移动通信系统仍存在较多关键问题需要研究,例如峰均比控制、多普勒频移消除等。其中,随机接入技术作为上行通信的第一步,极大地影响上行链路的用户接入性能,是基于LTE的卫星移动通信系统的研究重点之一。
LTE系统采用具有恒幅零自相关特性的ZC(Zadoff-Chu)序列作为接入前导序列,并且依据不同的小区半径设计了4种前导格式,用于完成上行定时提前(Time Advance,TA)估计。由于卫星移动通信系统具有更广的波束覆盖范围和更大的传播时延,现有的适用于陆地LTE系统的随机接入前导将不再适用,需要根据卫星通信特性进行重新设计。针对这一问题,文献[4-5]根据卫星通信的特点重新设计了接入前导。文献[4]采用LTE随机接入前导格式和序列生成原则,设计了具有更长持续时间的ZC序列用于上行接入,但是持续时间的增大引起子载波间隔减小,从而使得该序列对载波频率偏移(Carrier Frequency Offset,CFO)非常敏感。文献[5]改进了现有的LTE前导格式,通过级联多个相同的且具有较大子载波间隔的短ZC序列来构成长前导序列,只能够进行小数倍短序列长度的TA估计,对于整数倍短序列长度的TA则需要重新发送额外的前导进行估计,不但降低了接入效率,也浪费了额外的时频资源。
另一方面,ZC序列良好的自相关和互相关性能受CFO影响较大,只能抵抗一个子载波间隔(1.25 kHz)内的CFO,而低轨卫星(Low Earth Orbit,LEO)通信系统具有较大的多普勒频移,传统的LTE随机接入前导检测算法的性能急剧下降,进而导致TA估计错误,因此需要设计能够有效抵抗CFO的随机接入前导检测算法。文献[4,6]提出的TA估计方法并没有考虑小数倍CFO对随机接入前导检测的影响,文献[7]提出的方法受离散傅里叶变换(Discrete Fourier Transform,DFT)点数影响较大。
针对上述前导设计和检测算法两方面的问题,本文首先提出多根长序列(Multiple Root Long Sequence,MRLS)的构建方法,然后基于MRLS前导序列提出一种基于多个短ZC根序列联合的差分检测算法,最后通过仿真验证了所提算法能够完全消除CFO对随机接入前导检测的不利影响。
2 随机接入前导设计
LTE随机接入前导设计分为前导格式设计与前导序列设计两部分,下面针对卫星通信特性对前导格式和序列分别进行设计。
2.1 前导格式
LTE随机接入前导序列格式如图1所示,包括循环前缀(Cyclic Prefix,CP)、前导(Sequence,SEQ)ZC序列以及保护间隔(Guard Time,GT)三部分,其中TCP、TSEQ和TGT分别表示CP、SEQ和GT的持续时间。前导序列的持续时间TSEQ与覆盖范围有关,并且前导序列的持续时间越长,其覆盖范围也会越大。LTE标准根据陆地移动通信系统的不同场景定义了4种随机接入前导序列格式,以适应不同的小区半径,最大可以支持的小区半径约为100 km,对应的序列持续时间TSEQ为0.8 ms。而卫星移动通信系统具有较大的传播时延和较广的波束覆盖范围,现有的随机接入前导格式无法满足卫星波束覆盖范围性能要求,因而需要对前导格式中TCP、TGT和TSEQ进行重新设计。

图1 随机接入前导格式Fig.1 The preamble structure for random access
以“铱星”系统[8]为例,其轨道高度为780 km,波束半径为334 km,轨道倾角86.4°,最小通信仰角8.2°,卫星覆盖边缘波束的最大往返时延差为4.39 ms。根据上述参数,利用文献[4]中卫星场景中的前导格式设计方法,可以得到具有图1格式的接入前导,且持续时间TCP、TGT和TSEQ分别为4.8 ms、4.8 ms、6.4 ms。值得注意的是,ZC序列持续时间变为陆地场景下的8倍,序列持续时间与子载波间隔互为倒数[4],那么子载波间隔变为原来的1/8,因此该ZC序列对CFO更加敏感。
为了增大子载波间隔,又考虑到与LTE系统兼容性,本文提出一种改进的接入前导格式MRLS,如图2所示。其中,长前导序列的持续时间为TSEQ,且由K个短ZC根序列级联而成。每个短ZC根序列的持续时间TSS继续沿用LTE中前导序列的持续时间0.8 ms,则每个短ZC序列的子载波间隔ΔfRA仍保持1.25 kHz不变,MRLS级联序列的持续时间TSEQ=KTSS。对于铱星系统参数,前导序列持续时间应为6.4 ms,即TSEQ=6.4 ms,此时需要K=8个短ZC根序列级联构成这种前导序列。

图2 改进的MRLS前导格式Fig.2 An improved MRLS structure of the preamble
按照本文提出的MRLS前导格式,图3给出了 MRLS的时频资源结构。与文献[4]的前导格式相比,MRLS所占子载波个数由短ZC序列决定,具有较大的子载波间隔,可以有效抑制CFO的不利影响。下面,我们依据这种前导格式进行序列设计。
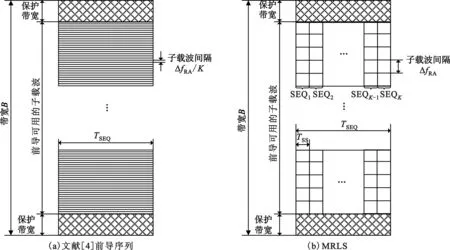
图3 前导序列时频资源格式示意图 Fig.3 The diagram of the preamble in time and frequency domain resource
2.2 前导序列
由于具有良好的零自相关和最小互相关性质,ZC序列被选择作为LTE随机接入前导序列,其定义如下[9]:
ZC(n)=e-jπun(n+1)/NZC。
(1)
式中:u值为ZC序列的物理根序列号索引,NZC=839为ZC序列的长度。根据图2所示的前导序列格式,长前导序列可以由式(2)所示的数学模型表示,即
(2)
式中:ZCk(n)表示第k个短ZC根序列,所对应的根序列号为uk,k=1,2,…,K。
文献[5]通过级联相同的ZCk(n)构建长前导序列,即u1=u2=…=uK=u。但是当使用本地序列ZC(n)对接收端前导检测时会产生K个峰值,只能得到小数倍TA值;而对于整数倍TA值,还需重新发送新的前导序列进行估计。由于星地间较大的往返时延,这种方法需要两次发送序列,不但增加了用户接入时延,还浪费了额外的时频资源。
为了克服重复级联序列的缺点,本文提出一种多根长序列MRLS,具体是利用K个不同的根序列级联构成前导序列,即u1≠u2≠…≠uK。由ZC序列的最小互相关特性可知,当利用本地的任一根序列进行滑动相关检测时,只能得到唯一的相关峰值。也就是说,不同于文献[5],利用MRLS前导序列可以通过“一步”检测得到完整的TA值,明显提升了用户接入效率。进一步,我们对这种序列进行检测算法设计。
3 随机接入前导检测算法
3.1 系统模型
当波束内的用户发起随机接入请求时,它会随机选择本地的一个长序列x(n)作为前导序列发送。当发送序列x(n)经过典型的卫星视距(Line of Sight,LOS)信道后,接收端收到的信号可以表示为
r(n)=ρx(n-τ)ej2πεn/NZC+ω(n)。
(3)
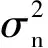
3.2 基于短ZC根序列联合差分检测算法
基于LTE的陆地移动通信系统采用循环移位限制和峰值合并的方法进行前导检测,只能承受一个子载波间隔内的CFO,在较大的CFO环境中检测性能会急剧下降。根据文献[7]所述,当CFO为子载波间隔的整数倍时,造成随机接入前导检测后的信号峰值位置发生偏移,其偏移量为du=(±1/u) modNZC;当CFO为小数倍子载波间隔时,峰值能量会分散到du的整数倍伪峰处,严重影响TA估计的正确性。而LEO卫星通信系统中的CFO可达20 kHz,远远大于单个子载波间隔,因此基于LTE的陆地系统中的随机接入前导检测算法不再适用于LEO环境。
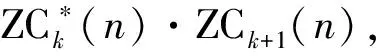
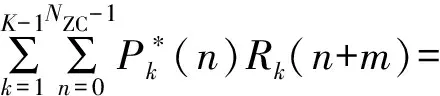
[r*(n+m+(k-1)NZC)r(n+m+kNZC)]。
(4)
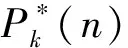
当m=τ时,将式(3)代入式(4)可得相关值序列Cp(m)如下所示:
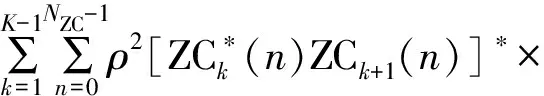
[x*(n+m-τ+(k-1)NZC)x(n+m-τ+kNZC)]×
e-j2πε(n+m-τ+(k-1)NZC)/NZCej2πε(n+m-τ+kNZC)/NZC。
(5)
由于把接收到的序列进行分段共轭相乘,频率偏移部分也进行共轭相乘,从而将频率偏移部分变为一常数项,即e-j2πε(n+m-τ+(k-1)NZC)/NZCej2πε(n+m-τ+kNZC)/NZC=ej2πε,如式(6)所示:
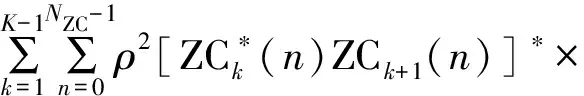
[x*(n+(k-1)NZC)x(n+kNZC)ej2πε]。
(6)
进一步将式(2)代入式(6),运算结果如式(7)所示:
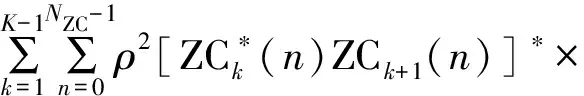
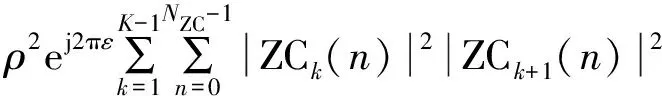
(7)
式中:|ZCk(n)|2和|ZCk+1(n)|2均为1,则Cp(τ)结果如式(8)所示:
Cp(τ)=ρ2ej2πεNZC(K-1)。
(8)
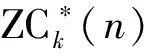
下面通过仿真验证短序列联合差分检测的相关特性,如图4归一化PDP谱所示。其中,信噪比为0 dB,传播时延τ为2.86 ms,对应于PDP谱的3 000个样点,归一化频率偏移ε为10.6。
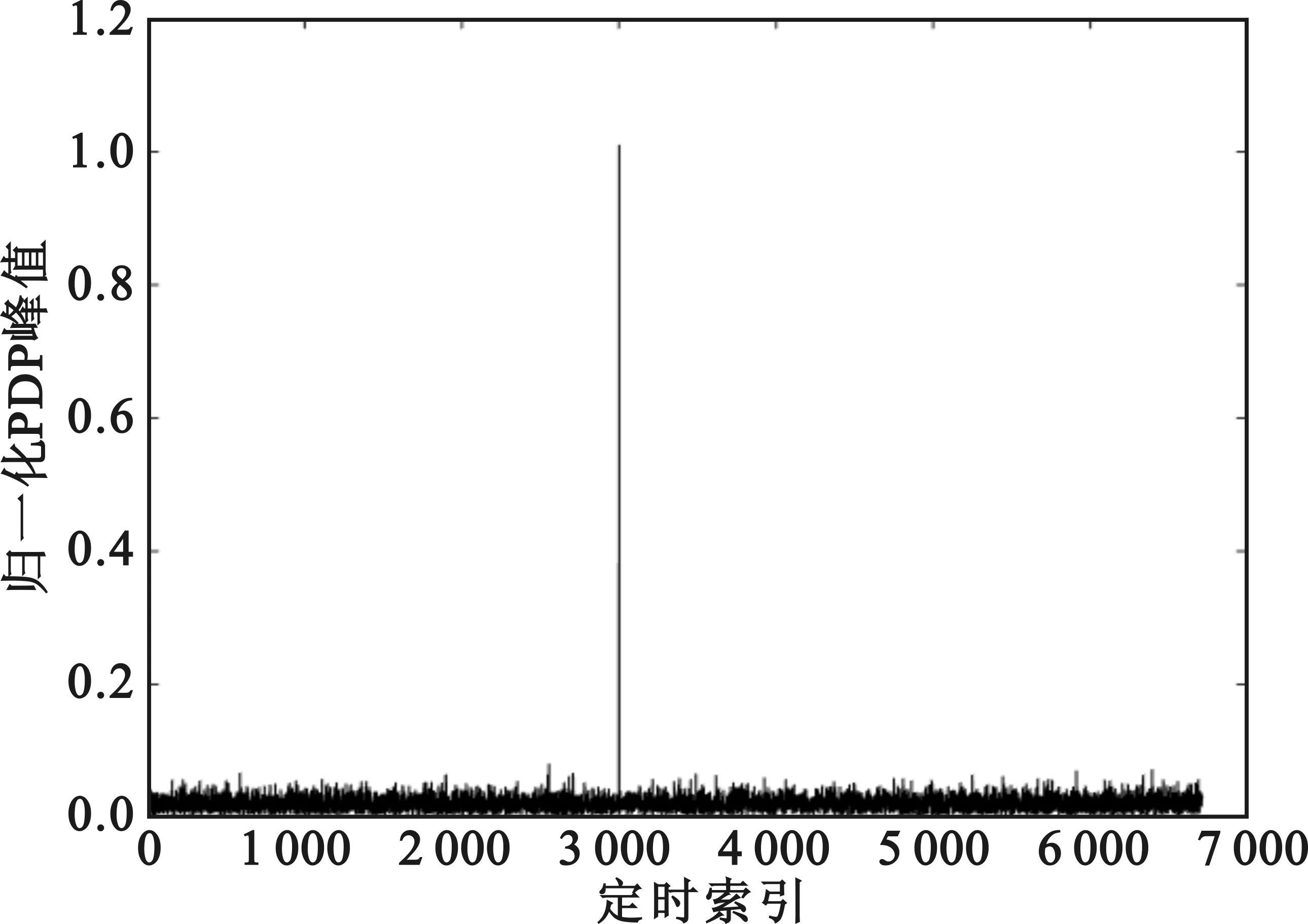
图4 归一化PDP谱Fig.4 Normalized PDP of the proposed metric
从图4中可以看出,当ε=10.6时,即同时存在整数倍和小数倍CFO的环境中,所提前导检测算法的PDP谱仍具有单一峰值且呈现脉冲的形式,并且峰值位置仍在正确的定时位置,并没有发生峰值位置偏移和峰值能量外泄。此外,当传播时延较大时,所提算法可以通过一次检测得到相关峰值用于TA估计,与文献[5]相比提高了接入效率。因此,仿真结果与理论分析一致,本文所提前导序列的检测算法在较大的CFO环境中能够保持较好的检测性能,为精确的“一步”TA估计提供了保障。
4 仿真分析
为了更好地说明本文所提算法具有良好抵抗CFO的能力,本节通过仿真分析验证该算法性能。以错误检测概率进行检测性能比较,包括本文所提算法以及4种对比算法。不失一般性,为了能够验证本文所提算法能够适用于LEO移动通信环境,仍以“铱星”系统为例,最大多普勒频移可达34.178 kHz[8]。在实际中,卫星移动通信服务大都在广大的开阔地面,这些场景大都是存在直射分量的地区,多径情况并不复杂,因此主要考虑LOS环境下加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道模型。具体仿真参数设置见表1。
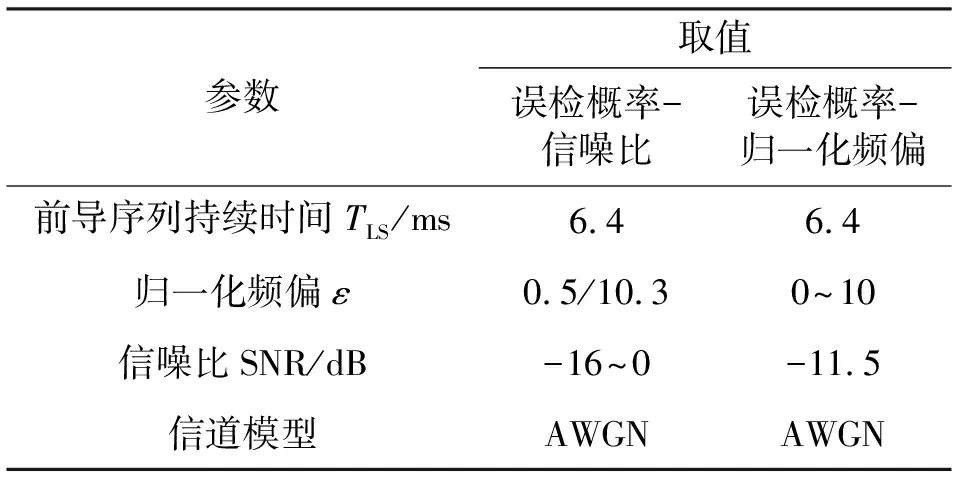
表1 仿真参数Tab.1 Parameter settings(EDP-SNR)
图5表示的是各随机接入前导检测算法在归一化频偏为0.5和10.3时的错误检测概率,可以看到,当ε=0.5时,基于LTE的陆地系统的随机接入前导检测算法误检概率约为50%,这是在小数倍CFO时峰值能量外泄,导致伪峰值增高,进而影响了正确的峰值位置提取;而在ε=10.3时,误检概率高达100%,由此可得陆地的随机接入前导检测算法只能忍受一个子载波间隔内的CFO,不能抵抗较大的CFO。文献[4,6]的随机接入前导检测算法在ε=0.5时误检概率保持在50%左右,这是由于这两种算法不能抵抗小数倍CFO,伪峰峰值较高,峰值检测对噪声较为敏感,不能有效检测到正确的峰值,定时估计的准确性较差。当ε=0.5且文献[7]所提的方法在DFT点数为序列长度时,小数倍CFO对其影响较大,其误检概率保持在50 %左右。而本文所提算法能够在小数倍CFO下实现精确定时估计,当SNR=-12 dB时,误检概率约为0.8%。当ε=10.3时,小数倍CFO较小,影响前导检测性能的主要因素为整数倍CFO,而文献[4,6]的前导检测算法能够抵抗整数倍CFO,所以能够保持较好的检测性能,当SNR=-12 dB时,文献[4,6-7]的误检概率分别约为3%、5%、8%,而本文所提算法的误检概率仅为0.8%左右。通过对仿真结果进行分析,可以得出所提算法相比于上述4种方法具有更好抵抗大CFO的能力。
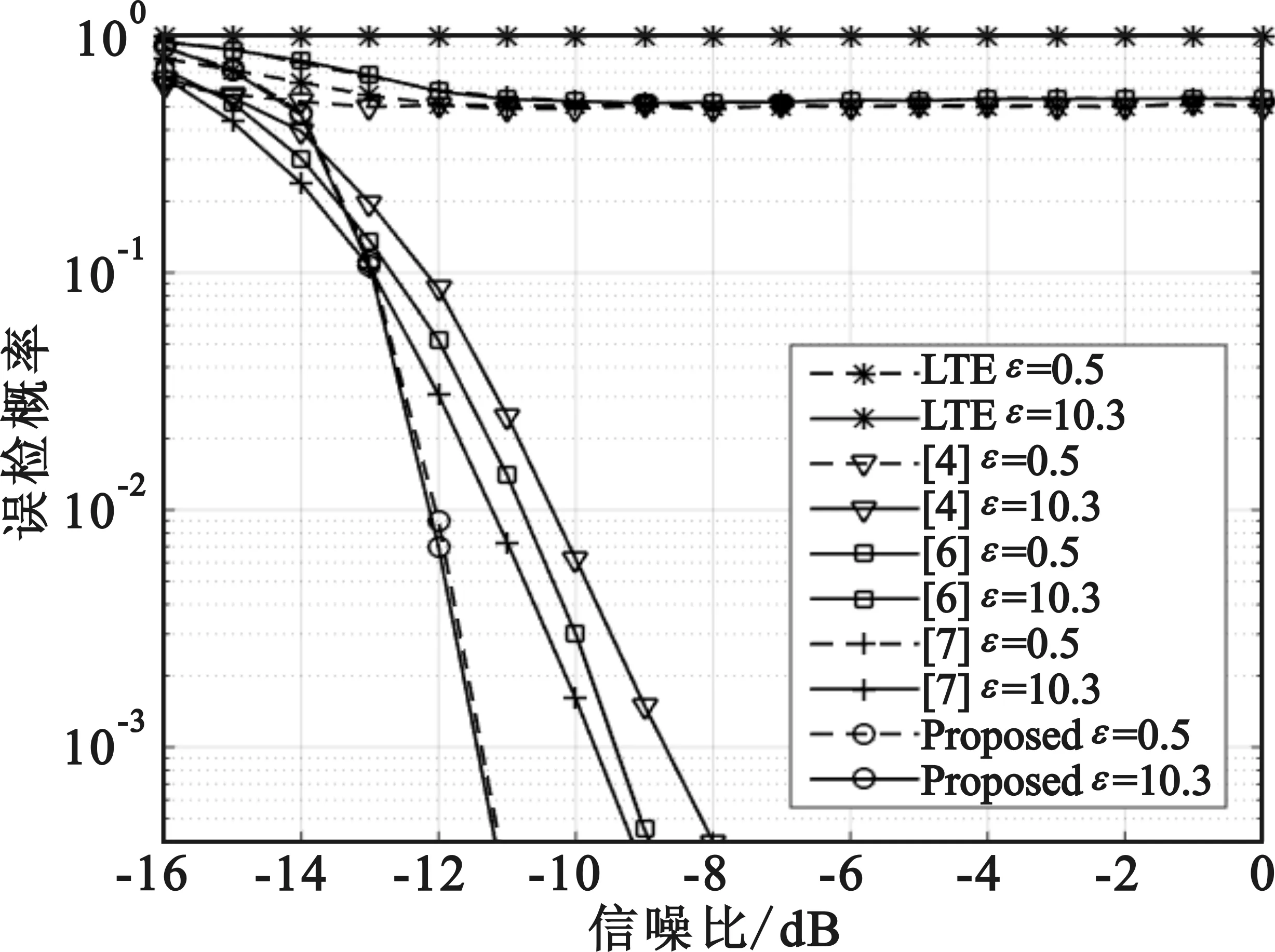
图5 不同信噪比下误检性能Fig.5 Detection performance comparison in different SNRs
图6表示的是各随机接入前导检测算法在信噪比为-11.5 dB时,不同归一化频偏下的误检性能仿真曲线。如图6所示,基于LTE的陆地随机接入前导检测算法的误检概率随着归一化频偏ε的增大而增大。当CFO大于1倍子载波间隔时,陆地的前导检测算法将无法正常工作,其误检概率达到100%。文献[4,6-7]的随机接入前导检测算法在只含有整数倍CFO环境中,误检概率较低,具有较好的检测性能,但存在小数倍CFO时,其检测性能会急剧下降,在小数倍归一化频偏为0.5时,误检概率最高约50%。而本文所提算法在不同频偏下其误检概率保持不变,约为0.1%。通过以上对比可以得出,所提算法相比于传统前导检测算法对CFO具有更好的鲁棒性。
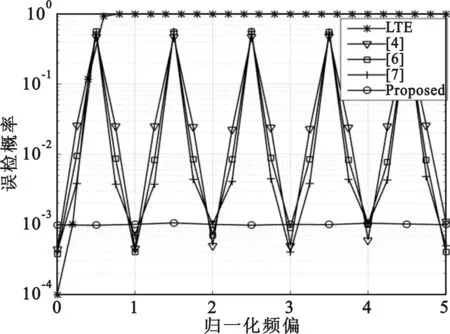
图6 不同归一化频偏下误检性能Fig.6 Detection performance comparison in different CFOs
5 结束语
本文研究了基于LTE的低轨卫星移动通信系统中随机接入前导序列设计及其检测算法。一方面,针对低轨卫星移动通信系统较广波束覆盖范围的特点,设计了一种具有不同根序列号的短ZC序列级联构成的MRLS前导序列,不仅支持较大的波束覆盖范围,而且可以有助于一步TA估计。另一方面,为了适用于具有较大多普勒频移卫星通信系统,根据MRLS前导序列,设计了一种随机接入前导检测算法,理论上分析了该算法可以利用共轭相乘的特性以及差分相关检测消除CFO对前导检测的影响。仿真结果与理论分析一致,本文所提算法能够对整数倍和小数倍CFO免疫,可以应用于具有较大多普勒频移的低轨卫星通信环境。
为了满足更大的覆盖范围,本文所提MRLS序列需进一步增加分段数,导致可用的接入前导数量减少,从而在一定程度上影响了用户的接入能力。另外,虽然仿真验证了所提算法的有效性,但是算法中由复数差分相关运算引入的计算量较大,可以考虑采用数值表示的方法降低复数乘法的计算量,从而进一步降低算法的整体运算复杂度。
