超高分辨率PolSAR图像去噪对极化特征的影响
2018-10-24
(1.广州铁路职业技术学院 信息工程学院,广州510430;2.广东工业大学 计算机学院,广州 510006)
1 引 言
对于极化合成孔径雷达(Polarimetric Synthetic Aperture Radar,PolSAR)图像的极化分解一直是雷达遥感数据处理领域的热点问题。一方面,极化分解是PolSAR图像数据和后续遥感应用之间的桥梁纽带,在实施极化分解后,能提取出被观测地物的特征参数,为后续的各种遥感应用提供输入参数。另一方面,由PolSAR的成像体系可知,相干斑噪声是一种固有噪声,会不同程度地影响极化分解的结果,实施相干斑降噪也会使得极化分解的输出参数产生不同程度的误差,这已经在诸多文献中得到验证[1-4]。文献[1]对非超高分辨率图像的极化分解窗口及相干斑降噪过程的影响进行了评测,得出了结论:为了得到最小误差的分解参数,分解窗口内至少要有60个独立采样像素点,一般采用9×9或者11×11的分解窗口尺寸。
近年来,随着世界各国机载、星载平台的不断升级换代,采集的数据空间分辨率逐渐提高,已达到或优于1 m的数量级,即分米级。对于空间分辨率为分米级的图像,通常称之为超高分辨率(Very High Resolution,VHR)图像。代表性的系统有德国宇航中心的F-SAR系统和美国喷气推进实验室(Jet Propulsion Laboratory,JPL)的UAVSAR系统[5-6]。对于非超高分辨率图像,现有传统模型及方法都有一个重要的前提假设,即分辨单元的空域尺度远大于雷达波长。然而,对于分米级的超高分辨率图像,分辨单元的空域尺度一般为0.1~1 m,不论是C频段、L频段,还是X频段,信号的电磁波波长都大于1 cm,均不满足这一假设[5-6]。
在超高分辨率背景下,已有若干学者建议对相干斑滤波处理算法对极化分解的影响重新进行定量评测[6];另一方面,合成孔径雷达图像的相干斑模型将趋向于不完全发展状态,已有学者对不完全发展状态下的非平稳相干斑进行了研究[7]。因此,本文评测的结果对于后续遥感地物分类算法的选择和应用有较大的指导意义。
2 PolSAR图像数据的表达及分解模型的选取
PolSAR系统测量的是具有正交极化状态的入射、散射电磁波的相关关系,此过程可用公式(1)表达,式中的矩阵即为散射矩阵,通常用字母S表达。散射矩阵的定义依赖于预先设定的雷达发射、接收天线极化状态,最常用的一对极化状态为水平、垂直极化状态,分别用字母H和V表达。散射矩阵中的任一元素S**为复散射回波值。对于比较常见的单基站环境,有互易定理成立,即有SVH=SHV,此时,散射矩阵是对称矩阵。为了后续的算法设计及实现的方便,将散射矩阵转换为向量的形式,向量k被称为Pauli目标向量,参见公式(2)。
(1)
(2)
由PolSAR系统的成像原理可知,对于具有稳定相干性的目标(或称为强散射目标),仅仅使用散射矩阵便可表达目标的散射特性;对于不具备稳定相干性的目标,只能用回波的统计特性来表达目标的散射特征,这就是相干矩阵(Coherency Matrix,CM),通常用字母T表达,参见公式(3):
T=E[kk*T]。
(3)
式中:算子E[]表示的是统计平均算子,上标*T表示的是共轭转置算子。
PolSAR图像数据的极化特征是通过极化分解得到的,限于篇幅,在此只对Cloude-Pottier分解、基于散射模型的分解、Touzi分解进行讨论。Cloude-Pottier分解属于非相干分解,是极化分解领域最经典的方法之一。Cloude-Pottier分解以相干矩阵为对象,通过矩阵的特征值分解,将相干矩阵分解成3个特征向量、3个特征值的线性组合,然后通过特征值的组合,得到最重要的2个极化分解参数,即特征角、极化熵,分别用字符α和H表示。这两个参数在地物分类应用中,几乎成为了标准化的工具[8]。
基于散射模型的分解是另外一大类极化分解方法,该类方法起源于弗里曼-德登(Freeman-Durden Decompositions,FDD)分解。该类方法都是基于散射对称性(Reflection Symmetry,RefSym)假设。RefSym假设有一个最大的缺陷:为了得到比较精确的分解结果,窗口尺寸必须满足最低数量要求[9]。已经有学者对由窗口尺寸导致的模型散射分解误差进行了若干实验验证,并得出了初步结论:为了抵消由RefSym假设带来的误差,空域平均窗口内一般至少要包含150~200个独立像素[9]。然而,现实应用中的FDD分解、Yamaguchi分解一般选取7×7或9×9窗口,这就导致分解结果存在较大误差。如果简单地扩大窗口尺寸为150,那么在实际应用中,窗口尺寸内会混杂不同类型的散射目标,也会同样带来较大误差。
Touzi散射向量模型分解是一种新型的分解方法,该方法最初是一种针对稳定散射目标的相干分解。该方法经过十多年的改进发展,整合了Cloude-Pottier分解非相干分解的部分概念,最终形成了一种兼容相干分解、非相干分解的方法。Cloude-Pottier分解方法中,有一个比较明显的不足:特征角参数α的二义性。参数α的二义性指的是属于不同散射机制的像素点具有相同的α值。这会导致后续分类算法无法区分这两类不同属性的地物。有文献给出了例证,如螺旋散射和二面角散射是两种不同的现象,但是却具有相同的特征角参数α值(π/2),因而,通过Cloude-Pottier分解无法区分这两种不同的散射现象[10]。为了解决特征角参数α的二义性,文献[1]引入了散射向量模型(Scattering Vector Model,SVM)以及对称散射类型(Symmetry Scattering Type,SST)这两个概念。在极坐标系下,SST的幅值和相位分别用字符表达αs、φαs,其定义参见公式(4),μ1和μ2分别为散射矩阵S的特征值。αs和φαs的取值区间分别限定为[0,π/2]和[-π/2,π/2]。对于任何的相干目标,给出以下散射向量模型SVM,参见公式(5)。
(4)
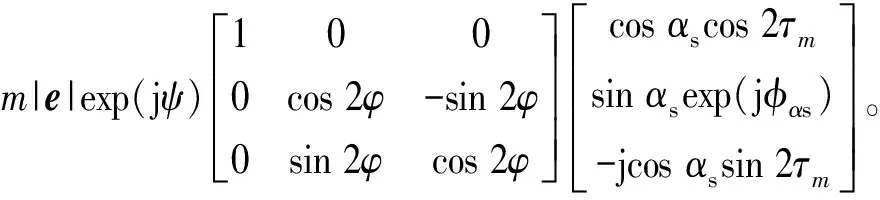
(5)
每一个相干目标都可以由公式(5)中的5个独立参数来表达,φ是目标朝向角,αs和φαs在公式(4)中已有定义,τm是目标的螺旋率,m为向量eSV与e的模的比值。除了目标朝向角φ以外,其他的4个参数都具有旋转不变性。此外,在公式(5)中,参数Ψ为绝对相位,该参数只是在干涉测量应用中发挥作用,因此在本文中不进行讨论。
将上述针对相干目标的散射向量模型与Cloude-Pottier非相干分解模型结合起来,可以得到一个消除参数二义性的非相干分解模型。首先,根据Cloude-Pottier非相干分解模型,任意散射目标可分解成3个独立的相干目标的相干矩阵之算术和,参见公式(6):
(6)
式中:λ1、λ2、λ3为相干矩阵T的3个特征值,通常会对这3个特征值做归一化处理。每一个相干矩阵Ti代表的是一种相干目标,矩阵的秩为1。具体实现时,可按如下步骤实施整合后的非相干分解:
(1)在一个空域窗口内计算目标散射矩阵T;
(2)对散射矩阵T实施对角化,得到3个特征向量及对应的特征值;
(3)对3个特征向量按模型(5)实施参数化,对于其中任意一个特征向量i,都可以表达为公式(7):
ICTDi=(λi,mi,φi,τ,αsi,φαsi)。
(7)
式中:ICTDi代表的是第i个特征向量的Touzi非相干分解。
3 实验验证及分析
本文选取了JPL提供的UAVSAR系统数据源,实验数据对应的观测地点为阿根廷圣菲省巴拉那河西岸的一座港口城市罗萨里奥(Rosario)。通过向JPL管理机构申请,获得了观测地点罗萨里奥对应的单视VHR图像,实验数据及UAVSAR系统的详细参数见表1。限于机器物理内存限制,仅截取2个子图,将2个子图经过Pauli编码后的伪彩色图像列出,分别参见图1和图2。图1中两块红色区域为待进行定量测试的均匀区域,分别记为Patch1、Patch2,对应的地物类型是沼泽灌木、湖面。图2中的红色区域Patch3对应的地物类型是农田。

表1 测试数据及系统参数Tab.1 The experimental data and system configuration parameters

图1 罗萨里奥单视数据伪彩色图像1Fig.1 The Pauli coded pseudo-color image of the single look complex data for the site Rosario No.1

图2 罗萨里奥单视数据伪彩色图像2Fig.2 The Pauli coded pseudo-color image of the single look complex data for the site Rosario No.2
本文实验选取了4种经典滤波方法为实验对象,分别为Sun、An-Yang、NM、LeeSig滤波器。Sun滤波主要采用了各向异性扩散方程滤波的原理,An-Yang滤波是一种结合预测试和非局部均值滤波原理的方法,NM滤波是一种仅采用了非局部均值滤波的方法,LeeSig滤波是一种经典的最小均方误差滤波方法。4种滤波器对应的功能实现都来自于欧洲航天局提供的开源极化SAR数据处理平台(PolSAR data processing and educational tool,PolSARPro),Touzi非相干分解工具来源于加拿大国土资源部遥感中心的极化工作站(Polarimetric Workstation,PWS)工具箱。4种经典滤波处理器的参数均设定为PolSARPro系统默认参数,经过滤波之后,将Patch1、Patch2、Patch3均匀区域的定量实验结果分别在表2、表3、表4中列出。误差的定量指标采用的是文献[5]中提出的一种绝对相对误差指标(Absolute Relative Bias,ARB),用符号Г表示,其定义参见公式(8):
(8)

根据极化Touzi分解的对称散射类型幅值和相位的取值区间,按照π/18为间隔均匀分区,得到9种不同的极化分解参数散射类型,分别用S0,S1,…,S8表示。表2~4中的符号×表示的是该区域无对应的散射机制像素点。经4种滤波器处理之后的对称散射类型相位的伪彩色编码图列于图3中。并从均匀区域Patch1中选取一个像素点,坐标为(X=2 621,Y=1 580),将其对应的滤波后的共极化特征图、交叉极化特征图列于图4和图5中。通过定量的实验结果可以看出,Sun滤波器因为采用了渐进式的滤波方式,可通过增加迭代次数逐步降低噪声水平。然而,该方法也会出现散射机制的混叠,例如,在表2第二行,经过Sun滤波后,散射机制S3消失;An-Yang滤波器和NM滤波器以及LeeSig均取得了相对较低的ARB误差;表4第二行,Sun滤波方法通过增加扩散次数获得了较小的ARB误差。总体来看,不同滤波器产生的ARB误差的差异较小,这正好验证了本文引言部分的假设,即超高分辨率SAR信号的电磁波波长接近于分辨单元的尺寸,相干斑噪声的影响明显变小。因而,对于极化分解窗口内的独立像素点要求也可相应地降低为7×7个,这可以使得极化分解窗口内混入异质像素的概率降低。

表2 Patch1区域的对称散射类型幅值ARBTab.2 The results of ARB for the amplitude of SST in Patch1

表3 Patch2区域的对称散射类型相位ARBTab.3 The results of ARB for the phase of SST in Patch2
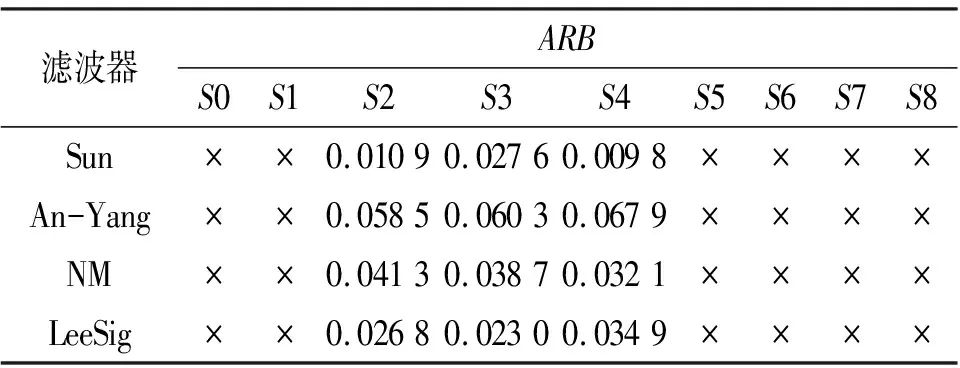
表4 Patch3区域的对称散射类型相位ARBTab.4 The results of ARB for the phase of SST in Patch3
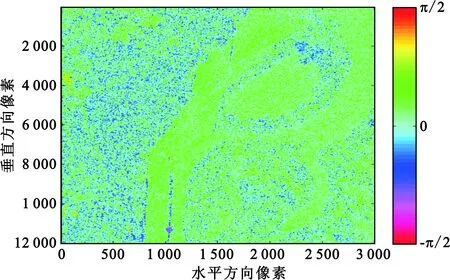
(a)Sun滤波

(c)NM滤波

(d)LeeSig滤波图3 对称散射类型相位的伪彩色编码图(滤波后)Fig.3 The Pauli coded pseudo-color image of the phases of SST(speckle filtered)

(a)Sun滤波-共极化
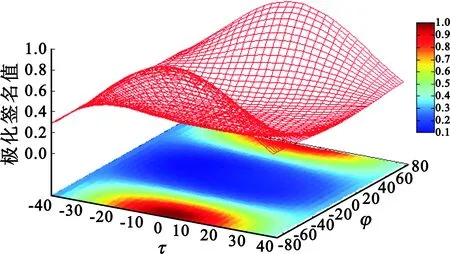
(b)An-Yang滤波-共极化

(c)NM滤波-共极化

(d)LeeSig滤波-共极化图4 均匀区域Patch1某像素点共极化特征图(滤波后)Fig.4 The co-polarimetric signatures of one pixel from Patch1(speckle filtered)
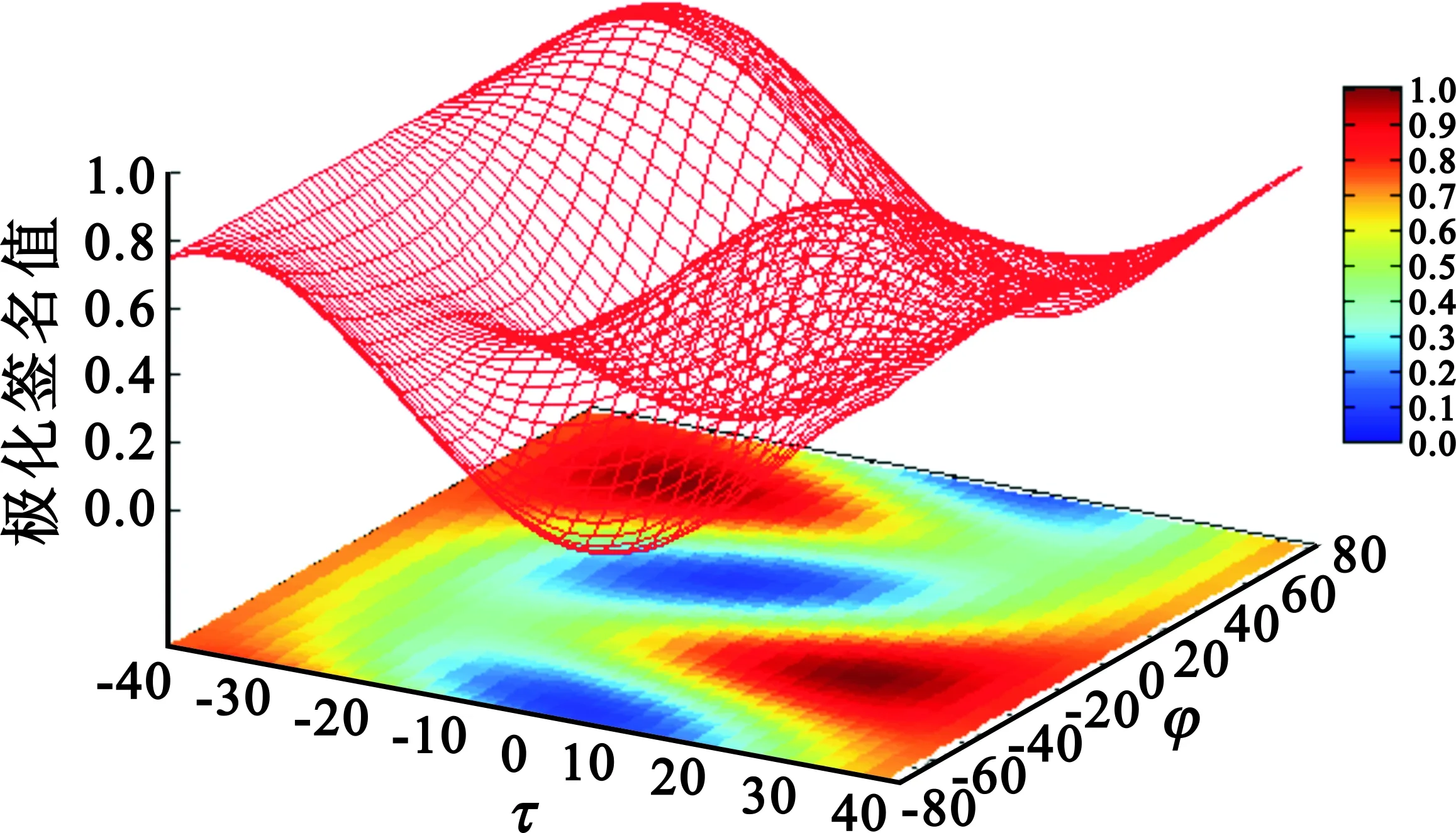
(a)Sun滤波-交叉极化

(b)An-Yang滤波-交叉极化

(c)NM滤波-交叉极化

(d)LeeSig滤波-交叉极化图5 均匀区域Patch1某像素点交叉极化特征图(滤波后)Fig.5 The cross polarimetric signatures of one pixel from Patch1(speckle filtered)
4 结束语
本文对超高分辨率SAR图像处理流程中的相干斑滤波对极化分解的影响进行了量化分析和实验验证。以Touzi非相干分解为实验对象,实施了4种经典的相干斑滤波处理过程,对滤波之后的数据选取了3块相对均匀的区域进行定量的ARB误差测定,结果显示,极化分解窗口尺寸的要求可降低为7×7,这可以使得极化分解窗口内混入异质像素的概率降低。测定结果对于后续遥感应用用户进行参数选择具有一定的参考意义。在下一步的研究中,可就相干斑滤波对于极化遥感地物分类精度的影响进行定量的测定。
