一种基于预测值量测转换的卡尔曼滤波跟踪算法
2018-10-24旭1吴小平1何子述
王 旭1,程 婷,吴小平1,何子述
(1.西南电子电信技术研究所,成都610041;2.电子科技大学 电子工程学院,成都611731)
1 引 言
在雷达目标跟踪中,系统的量测信息通常在球坐标系得到的,包括目标的距离、方位角和俯仰角量测信息,而目标运动状态方程是建立在直角坐标系的,显然这些量测信息与目标状态向量呈非线性关系。因此,基于该信息的目标跟踪是一个非线性估计问题,无法直接采用经典的卡尔曼滤波。
针对这一问题可采用扩展卡尔曼滤波算法[1],但该算法仅在量测误差较小时能获得较好的跟踪效果,量测误差增大时跟踪精度下降甚至发散。基于样本点的算法,例如不敏卡尔曼滤波方法[2]和粒子滤波算法[3-4],虽然能获得较好的跟踪效果,但是算法的运算量较扩展卡尔曼滤波算法大,尤其是粒子滤波算法。基于量测转换的卡尔曼滤波(Converted Measurement Kalman Filter,CMKF)算法是解决这一问题的另一种思路,即将量测值从极坐标转换到直角坐标系下,转换为线性估计问题,再采用标准卡尔曼滤波算法进行状态估计。利用极坐标和直角坐标系之间的变换关系可以直接实现量测转换[5],但这种转换方式是有偏的[6]。文献[6]提出了去偏量测转换(Debiased Converted Measurement,DCM),采用加性去偏的量测转换方式,即将传统量测转换结果减去其均值,从而保证了转换量测的均值是无偏的,但是在求取量测转换误差统计特性时以量测值为条件。文献[7]指出传统量测转换方法的偏差实质是乘性的,因此提出通过乘以一个偏移因子实现去偏,提出了无偏量测转换(Unbiased Converted Measurement,UCM)方法,但该方法在计算量测转换误差统计特性时存在兼容性问题[8]。基于此,文献[8]提出了改进的UCM(Modified Unbiased Converted Measurement,MUCM)算法,虽然其克服了UCM的问题,但是在该算法中求取量测转换误差统计特性时以量测值为条件,这使得后续卡尔曼滤波算法中的增益矩阵与量测误差相关,最终导致状态估计结果的有偏性。上述对目标位置量测信息的量测转换方法,也是同时基于目标位置和径向速度量测信息进行目标跟踪的基础[9]。文献[10]中将DCM和序贯滤波相结合依次处理目标位置量测信息和径向速度量测信息。文献[11]中采用DCM处理目标位置量测信息,并利用静态融合方法处理径向速度量测信息。可见,量测转换方法的研究对于同时具有位置和径向速度量测时的目标跟踪问题也具有实质性意义。
现有量测转换方法主要的区别在于量测转换方式以及计算量测转换误差统计特性的方法。考虑到传统量测转换的偏差实质为乘性的,本文将采用UCM的量测转换方式,同时为克服UCM中计算量测转换误差统计特性方法的不兼容问题,对MUCM方法进行改进,提出以目标预测值为条件计算量测转换误差的统计特性,克服滤波参数与量测误差之间的相关性,从而保证最终目标状态估计结果的无偏性。将该量测转换方法与卡尔曼滤波算法相结合,最终获得了一种基于预测值量测转换的卡尔曼滤波跟踪算法。仿真结果表明了本文算法的有效性。
2 问题描述
考虑一个三维目标跟踪场景,令r、β和ε分别表示在球坐标系下的真实目标距离、方位角和俯仰角,用rm、βm和εm表示相应的量测值,则真实值和量测值之间有下面的关系:
(1)
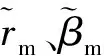
(2)
显然,上述量测信息与目标运动状态之间呈非线性关系,量测转换方法旨在笛卡尔坐标系下建立如下量测方程:
Zc(k)=H(k)X(k)+Vc(k) 。
(3)
式中:Zc(k)为k时刻笛卡尔坐标系下的转换量测值;H(k)为量测矩阵;X(k)为目标在k时刻的状态向量;Vc(k)表示k时刻在笛卡尔坐标系下的转换量测误差,通常为零均值高斯白噪声,其相关矩阵为
(4)
利用非线性量测信息,不同的量测转换方法将获得不同的转换量测值,并计算相应的量测转换误差的统计特性。
3 基于预测值量测转换的跟踪算法
由于本文量测转换方法是在MUCM算法基础上提出的,因此为确保结构的完整性,先对MUCM方法进行简单回顾,随后分析MUCM方法的不足之处,并给出基于预测值量测转换的方法。
3.1 修正的UCM方法
在传统的量测转换方法中,根据球坐标和直角坐标系之间的转换关系,容易得到[5]
(5)
将式(1)代入到式(5)中,然后对笛卡尔坐标系下的转换量测值x、y和z求数学期望可以得到[7]
(6)
可见,该量测转换方法是有偏的。根据式(6),给出如下无偏转换量测(UCM)Zc(k)[7]为
(7)
MUCM方法采用上述量测转换方式,在计算量测转换误差统计特性时,令[8]
(8)

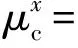

(9)
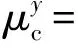

(10)
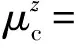

(11)
相应地,基于量测值的转换量测误差的协方差矩阵Rc按下式计算[8]:
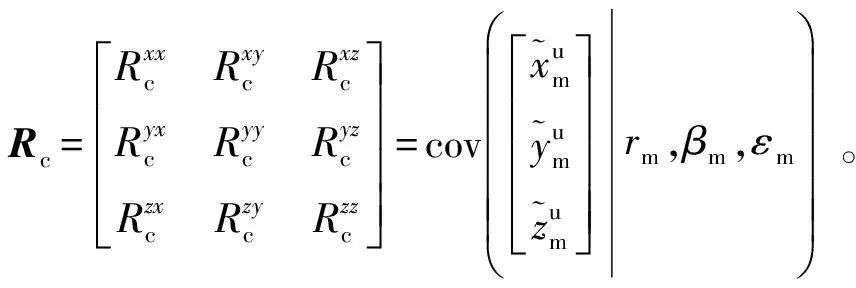
(12)
3.2 基于预测值的量测转换方法
MUCM在计算转换量测误差的均值和协方差矩阵的时候都是利用量测值来计算的。这种计算方法会导致协方差矩阵和量测噪声相关,进一步会使卡尔曼增益依赖于量测噪声,使得经过卡尔曼增益加权后的量测噪声的均值不为零,最终导致状态估计无法保证无偏性。为了解决此问题,现考虑基于目标预测位置计算量测转换误差的均值和方差。
目标距离、方位角和俯仰角的预测值表示如下:
(13)
根据式(1)和式(13),容易得到
(14)
(15)
利用式(14)和式(15),基于目标预测位置,可以得到转换测量误差的均值为
(16)
相应的转换量测误差协方差阵RCp为
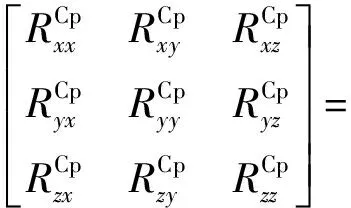
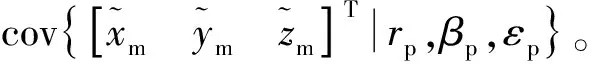
(17)
由式(17)推导求得的对应的RCp的各元素具体如下:

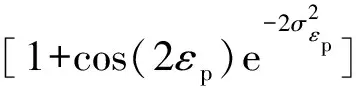
(18)
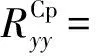
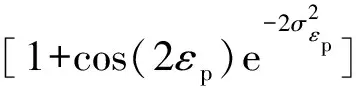
(19)
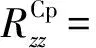

(20)
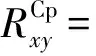
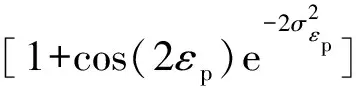
(21)


(22)
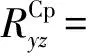

(23)
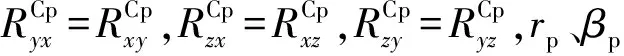
基于式(7)的量测转换结果,以目标预测位置为条件计算出量测转换误差为零均值,方差满足式(17)~(23)。由于式(7)所示的转换结果已经是直角坐标系中目标在3个方向的位置信息,显然已经与目标状态向量之间呈线性关系了,因此可以在此基础上运用卡尔曼滤波。将上述量测转换方法与卡尔曼滤波算法相结合,即可获得一种基于预测值量测转换(Predicted Position based UCM,PPUCM)的卡尔曼滤波目标跟踪算法。
4 仿真分析
考虑一个在平面做匀速直线运动的目标,雷达位于坐标原点,其采样间隔为1 s。目标的初始位置为(5 5 5)km,初始速度为(25 25 0)m/s,现根据距离、方位角和俯仰角的量测精度,考虑3个不同的场景,具体参数如表1所示。这3个场景分别代表量测精度较好、一般和较差的情况。
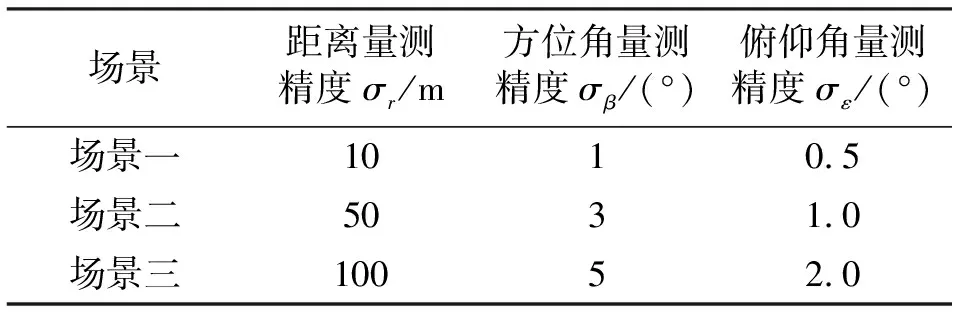
表1 仿真场景参数Tab.1 The parameters of simulation scene
采用本文提出的基于预测值量测转换的卡尔曼滤波算法对该目标进行跟踪,并对其性能进行统计,以下仿真结果均为100次蒙特卡洛仿真的统计结果。为说明本文算法的有效性,同时也采用UCM以及MUCM对其进行跟踪,并将三者的跟踪精度在不同的仿真场景下进行对比。图1给出了3个场景下3种算法跟踪结果的位置RMSE曲线。
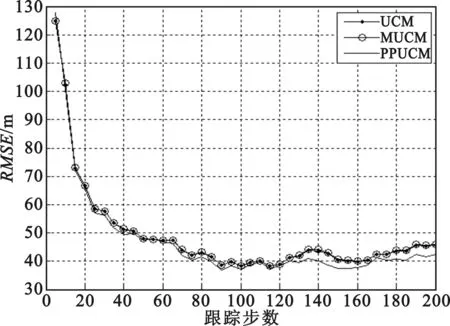
(a)场景一

(b)场景二

(c)场景三图1 3种基于量测转换的卡尔曼滤波算法精度比较Fig.1 The precision comparison among three algorithms of measurement conversion based Kalman filter
由图1可见,在3个仿真场景下,本文提出的方法PPUCM均能获得最小的RMSE值,即能获得更好的跟踪效果,而UCM和MUCM两者性能相当,仅在场景三中量测精度较差时MUCM才体现出相对于UCM的优势。本文算法不仅在3个场景下均体现出更好的性能,而且跟踪精度较传统算法的改善程度随着场景中量测误差的增大而变得更加明显。在场景三中,PPUCM的跟踪精度较MUCM提升近20%,较UCM提升超过20%,其原因在于,PPUCM方法在量测转换过程中以预测值为条件计算量测转换误差的均值和方差,避免了UCM计算中的不兼容性,也克服了MUCM计算中利用量测值为条件而导致的滤波增益与量测误差相关的问题。进一步,我们对比了3种算法的时效性,如表2所示。

表2 3种算法运行时间比较Tab.2 The compare of run time among three algorithms
从表2可见,UCM的耗时最短,MCUM和PPUCM的耗时相当,但3种算法的运行时间在同一个量级上,这说明了本文算法能在不增加运算量的同时有效提高目标跟踪精度。
5 结束语
实际目标跟踪系统中,量测数据通常是在球坐标系中获得的目标量测位置,该信息与目标运动状态之间的非线性特性导致不能直接采用卡尔曼滤波进行跟踪。量测转换方法是解决这类问题的一个有效途径,但传统的转换方法在计算量测转换误差统计特性时以目标量测值为条件,导致了滤波增益与量测误差的相关性,使得最终估计结果为有偏估计。针对这种情况,本文提出基于目标预测位置计算量测转换误差的均值和方差,克服了传统量测转换的缺陷,并与卡尔曼滤波算法相结合,实现了目标的有效跟踪。仿真表明,本文算法能在不增加运算量的条件下获得较传统量测转换方法更好的跟踪效果,跟踪精度改善度达20%,是一种有效的量测转换目标跟踪方法。后续研究中,将进一步考虑目标的机动特性和系统的径向速度量测信息,发展可同时处理径向速度量测的机动目标跟踪算法。
