±800 kV特高压直流大跨越悬垂绝缘子 串均压方案优化
2018-10-24,,
, ,
(1.国网山东省电力公司,济南 250001; 2.山东电力工程咨询院有限公司,济南 250013)
0 引言
绝缘子串运行于导线与横担间极为复杂的电场环境中,这就决定了沿绝缘子串场强和电压分布的不均匀性。在理论定性分析时,前苏联专家T.H.亚历山大罗夫认为绝缘子所连接的高压端和低压端分别为两个电极,高压端带有电荷,低压端带有相反电性的感应电荷。基于这种思想,总结研究出一套沿绝缘子串场强分布的解析公式。靠近导线的高压端绝缘子承受的电压百分比最高,随着离开高压端的距离增大,电场强度减弱,绝缘子承受的电压百分比降低,当十分靠近铁塔横担低压端时,电场线受低压端金具畸变作用,再次汇集导致电场强度再次小幅增大。然而解析公式未能充分考虑铁塔、大地、金具等影响因素[1]。
目前国内外进行的相关研究多集中在超高压及特高压交流领域,对直流线路的相关研究也主要以普通线路(相对于大跨越)使用的合成绝缘子为研究对象。直流线路大跨越高跨塔采用的悬垂绝缘子串与普通段线路大不相同,普通段一般采用V形合成绝缘子串[2-3],而大跨越则采用四联或六联I形瓷绝缘子串,加之大跨越工程并不常见,国内外对直流线路大跨越超长、复杂绝缘子串电场及电位分布的系统研究较为少见。
与交流线路相比,直流线路的绝缘子更容易积污,在相同的污秽等级下,直流线路绝缘子的配置数量往往比交流增加约20%,由于直流线路绝缘子串的长度更长[2],这进一步加剧了单片绝缘子承受电压的不均匀程度。绝缘子上的最大压降与平均压降的比值称为不均匀系数。如果保持导线和杆塔结构不变,则绝缘子串长度增加,不均匀系数增加。当串长增加到5 m时,不均匀系数趋于常数。随着电压等级的增高,盘式绝缘子上的电压降问题更加突出。
随着计算机技术的发展,基于有限元的仿真广泛应用于绝缘子串的电场的数值计算[4]。国内王景朝等建立了1 000 kV特高压交流线路的绝缘子串的电位分布,通过计算均压环的管径、环径和屏蔽深度,确定了均压环安装在高压侧的第2片和第3片绝缘子之间,均压环环径取120 mm时,均压效果较好,并通过试验验证了计算结果[5]。
黄道春等建立三维有限元模型,分析了铁塔、导线、连接金具、联板及相间缘子串对瓷质绝缘子串电压分布和电场强度的影响程度。其研究结论表明,为减小计算规模、提高计算效率,可对三维模型进行适当简化,但导线和铁塔的影响不可忽略,导线的长度可控制在一定范围内(大于14 m),铁塔可用不镂空的塔窗代替整基铁塔;联板和金具等金具的影响较小,可用形状简单的模型代替;简化后的模型能够保证剖分密度和计算精度[6]。
本文将根据国内外的最新研究成果[7-13],针对特高压大跨越复杂悬垂绝缘子串的特点,利用有限元计算软件ANSYS建立三维模型,并对模型进行适当简化,并利用最优化理论分析取得最佳均压方案。
1 三维模型的建立及合理简化
1.1 计算模型
在三维电场中,以标量Φ电位作为待求量,以正确的边界条件做为定解条件,三维电场所满足的方程式如下[6]。
·(εrε0Φ)=-ρv
(1)
式中:Φ(x,y,z)为三维的标量电位,εr(x,y,z)为三个方向矢量上的相对介电常数,ε0为真空的介电常数,ρv(x,y,z)为体电荷密度。
在有限元计算时,首先求解三维标量电位,然后根据麦克斯韦微分方程组直接得到电场强度E和电位移矢量F。
E=-Φ
(2)
F=εrε0(-Φ)
(3)
由于整体模型的几何形状在沿铁塔中心剖面上严格对称,为可以减小模型的尺寸、节省计算资源,计算时采用对称边界条件。在沿线路方向的中心剖面上,左右两极几何形状相同,仅电压极性相反,可采用奇对称边界。在垂直线路方向的中心剖面上,前后侧几何形状及电压激励均相同,可采用偶边界条件。
笔者以山西-江苏±800 kV特高压直流输电线路黄河大跨越工程为依托,根据工程实际的杆塔、绝缘子、金具及导线等结构建立模型。绝缘子为550 kN瓷三伞型,每串四联,每联81片;导线采用JLHA1/G4A-900/240特强钢芯铝合金绞线,四分裂,分裂间距600 mm。瓷绝缘子的钢帽及钢钉按实际尺寸建模,并把空气的影响考虑在内。
图1 局部计算模型Fig.1 Local calculation model
根据输电线路外绝缘设计技术要求,绝缘子串应在工作电压、操作过电压和雷电过电压下可靠运行。直流绝缘子片数选择主要取决于工作电压下的污秽耐压特性,一般是根据污秽性能选定绝缘子片数,再校核计算操作及雷电冲击性能[3]。本文研究的绝缘子串片数每联达81片,经校核整串可耐受设计规范规定的1.6倍操作过电压及250 kA雷电流的冲击,且直流线路操作和雷电过电压出现的概率很低,因此本文研究绝缘子串在工作电压下的电位分布。
1.2 计算结果与分析
参考王景朝、黄道春等的研究成果,本文以均压环安装在第2片及第3片绝缘子之间,均压环环径取120 mm为原始条件进行计算[5-6]。为提高运算速度,采用对称边界建立1/4模型,在此基础上通过分析论证,进一步优化均压方案。

图2 绝缘子串高压端中心剖面的电位分布云图Fig.2 Potential distribution in the central section of insulator string
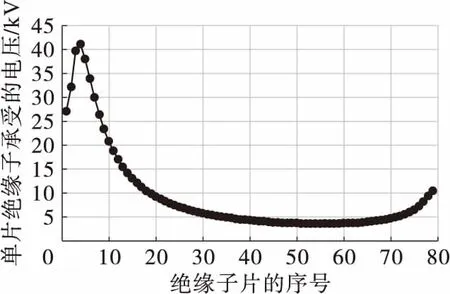
图3 沿绝缘子串的电位分布图Fig.3 Potential distribution of insulator strings
由图2、图3可知,第4片绝缘子承受的电压最大,为40.97 kV,占整串总电压的5.12%,前10片绝缘子承担的电压占整串总电压的48.7%。随着逐步远离高压端的带电体,电场线逐渐分散,绝缘子表面的场强逐渐降低,单片绝缘子承受的电压逐步减小,靠近铁塔横担时,因电场线再次聚集,致使低压端的绝缘子承受的电压略有升高。高压端附近的绝缘子承受的电压较高,本文后续将对前20片绝缘子的电压分布进行重点分析。
以国内某绝缘子厂家生产的550 kN三层伞形瓷绝缘子U550BP/240T为例,厂家提供的正极性直流1 min湿耐受电压为60 kV,然而受自然界污秽的影响,实际运行中绝缘子的污秽湿闪电压低于实验值。T.H.亚历山大罗夫认为,现代盘式绝缘子可以在工频电压不超过40 kV的范围内使用,本文以单片绝缘子承受的最大电压40 kV作为绝缘子可靠运行的判据。
金具起晕场强的取值,根据PEEK公式计算,约为30 kV/cm,工程建设时为考虑一定安全裕度,1 000 kV交流特高压示范工程取20 kV/cm~23 kV/cm,本文将以20 kV/cm作为均压环不发生电晕的判据。
经计算,空间场强的最大值出现在均压环和屏蔽环的外侧,最大值为11.15 kV/cm,满足不发生电晕的场强要求。金具及导线周围的电场显著减小,均压环和屏蔽环起到很好的屏蔽效果。
2 均压环安装位置对电压分布的影响
由图4、表1可知,随着均压环屏蔽深度的增加,绝缘子承受的最大电压逐步降低,除第2、3片之间的安装方案外,其余方案的绝缘子承受的最大电压均小于40 kV,均压环表面最大场强小于20 kV/cm。
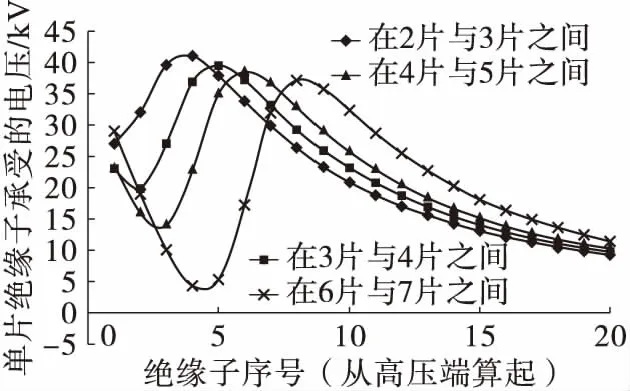
图4 均压环安装位置H对绝缘子承受电压的影响Fig.4 Effect of grading ring parameter H on the insulator withstand voltage

安装位置(H)绝缘子承受的最大电压/kV电压不均匀系数均压环表面最大场强/kV·cm-1第2、3片之间(H=570mm)40.974.1511.154第3、4片之间(H=810mm)39.564.0110.994第4、5片之间(H=1 050mm)38.553.9011.789第6、7片之间(H=1 530mm)37.243.7714.835
增加屏蔽深度有利于改善均压效果,如果过于追求增大均压环屏蔽深度,会为工程设计带来两方面的不利影响:第一,风偏后带电部分对塔身的空气间隙减小,导致铁塔横担加长,增加工程投资。第二,整支绝缘子串的干弧距离缩短,对整串的绝缘性能产生不利影响。
综合考虑以上因素,均压环可安装在第3、4片绝缘子之间。
3 均压环环径D对电压分布的影响
均压环环径D和管径d如图5所示。

图5 均压环参数环径D与管径dFig.5 grading ring parameter D and d
取均压环安装在第3、4片绝缘子之间(H=810 mm),管径d=120 mm,对不同环径D对电压及电场分布的影响进行计算。
如果均压环环径过大,同样导致风偏后带电的均压环对塔身的空气间隙减小。
由图6及表2可知,均压环环径对电位及均压环表面最大场强的影响较为明显,并根据表2的计算结果,环径D取2 000 mm较为合理。

图6 均压环环径D对绝缘子承受电压的影响Fig.6 Effect of grading ring parameter D on the insulator withstand voltage
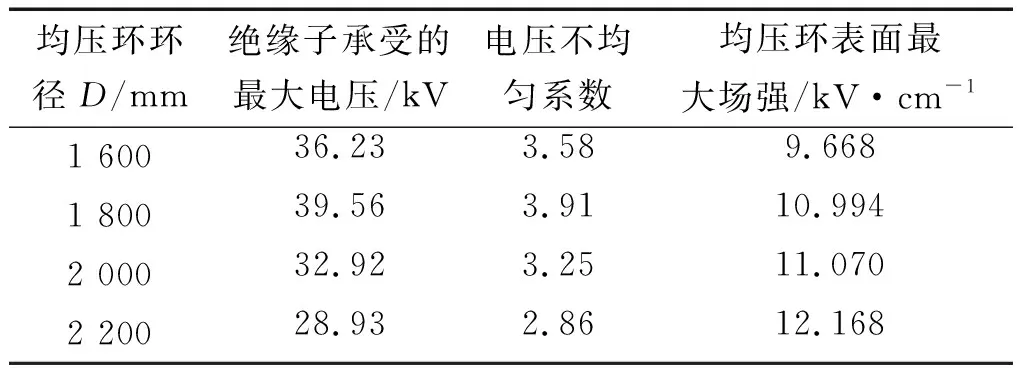
均压环环径D/mm绝缘子承受的最大电压/kV电压不均匀系数均压环表面最大场强/kV·cm-11 60036.233.589.6681 80039.563.9110.9942 00032.923.2511.0702 20028.932.8612.168
4 均压环管径d对电压分布的影响
由图7及表3可知,均压环管径d对电位及均压环表面场强的影响较小,管径取120 mm可满足要求。
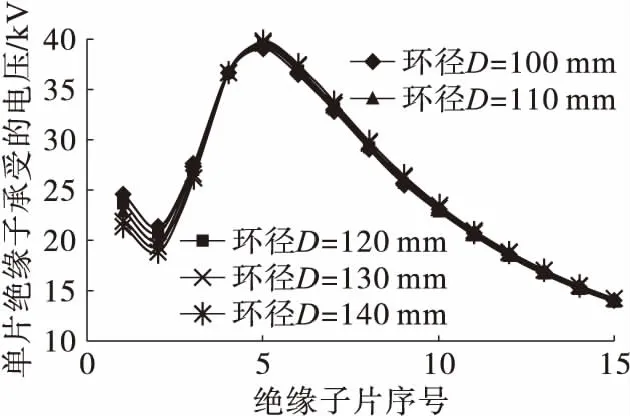
图7 均压环管径D对绝缘子承受电压的影响Fig.7 Effect of grading ring parameter D on the insulator withstand voltage

均压环管径d/mm绝缘子承受的最大电压/kV电压不均匀系数均压环表面最大场强/(kV·cm-1)10039.013.9511.29511039.323.9811.17212039.564.0110.99413039.634.0110.69914039.774.0310.487
5 基于多变量非线性的最优化分析
分别保持均压安装位置H、环径D及管径d三个参数中的两个不变,变化另一个参数,分别求得了三个参数在其它参数固定情况下的最优值,然而这三个参数最优值的组合不一定是使绝缘子沿面场强最小的情况。
本文建立的三维模型复杂,单片绝缘子承受的最大电压和均压环的三个参数间存在一种映射关系F,而非是一种具有解析表达的函数关系,其映射关系表述如下所示:
U=F(H,D,d)
(4)
式中,U为单片绝缘子承受的最大电压。
综合考虑工程建设实际情况,把H、D及d的取值范围限定在合理区间,将H取值在[570,1 530],D取值在[1 500,2 400],d取值在[90,150],该优化问题成为一个多变量非线性有约束的目标最优化问题,优化目标是取一组H、D、d使U取得最小值。
鉴于本文的优化目标函数难以用解析式表达,目标函数的导数难以取得,本文采用模式搜索算法[13]进行求解。模式搜索首先求解出初始点的值,然后按照一定的规则在改点周围寻找一系列的点,比较大小,获得比改点值更小的点,根据该规则不停的寻找比上一次更小的点,使之越来越靠近最优值,直到在某值域内寻找不出比改点更优的点为止。
利用模式搜索算法进行优化求解,经过13次迭代,求解收敛至设定精度,最终优化结果为H=930.4 mm、D=2 083.7 mm、d=117.6 mm,单片承受最大电压为38.63 kV,绝缘子绝缘子串表面最大场强值为1.627 kV/cm,均压环表面最大场强为10.925 kV/cm。工程实际中,可使均压环安装在第3、4片绝缘子之间,均压环环径取2 050 mm,管径取120 mm,参数优化的效果如表4所示。
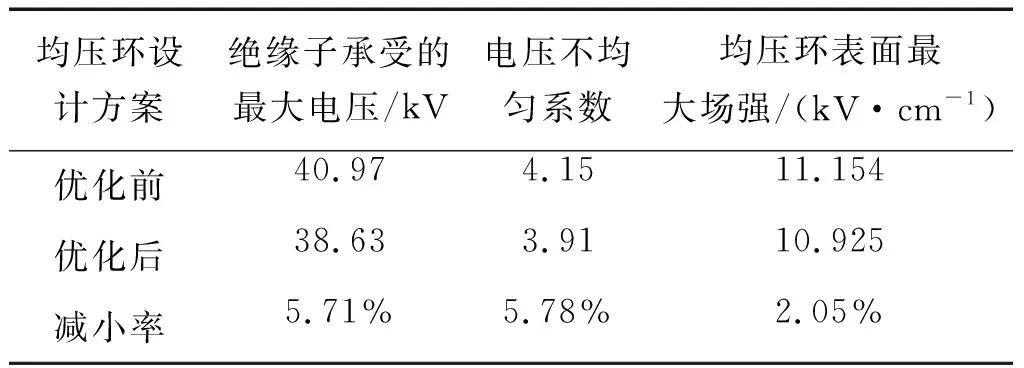
表4 均压环优化前后的电压及电场对比Table 4 Comparison of voltage and electric field before and after grading ring parameter optimization
由表4可知,与优化前相比,单片绝缘子承受的最大电压降低约5.71%,均压环表面的最大场强降低约2.05%。
6 结论
本文在国内外最新研究成果的基础上,建立三维有限元模型,对±800 kV特高压大跨越复杂悬垂金具绝缘子串的电位及场强分布进行系统研究,并利用多变量有约束的最优化理论,对均压环的参数进行最优化设计,主要结论如下:
1)均压环屏蔽深度H置及环径D对电位及场强的分布影响较为明显,而均压环管径d的影响并不显著。
2)优化后的均压环安装在第3、第4片绝缘子之间,均压环环径D取2 050 mm,均压环管径d取120 mm。
3)与优化前相比,单片绝缘子承受的最大电压降低约5.7%。
4)优化后,单片绝缘子承受的最大压降满足长期安全运行的要求(小于40 kV),均压环表面不发生电晕(小于20 kV/cm)。
