基于MFOA的输电线雷击定位算法研究

(国网利津县供电公司，山东 利津 257400)

0 引言

高压输电线路是电路系统中的重要部分，但因其大多暴露在外而常会受到雷击。若不能及时找到雷击点，则会对人们生活、工作造成严重的影响。因此，对输电线路雷击位置准确定位，及时恢复输电线供电，具有重要的意义。但目前雷电定位系统(lightning location system，LLS)中所用到的定位迭代算法，具有收敛效果受初始值影响大的缺点[1]。针对此问题，笔者提出了一种基于MFOA的输电线雷击定位算法。该算法对FOA进行改进，使其能够较好地收敛到全局最优解。然后基于FOA不断缩小检测位置与雷击位置之间距离的误差，从而实现输电线雷击定位，得到雷击点的坐标。该算法弥补了现有雷电定位算法的不足。

1 雷电定位系统

1.1 雷电定位系统研究现状

目前，我国大多数省内建立了能够及时定位雷电位置的LLS，以便应用于航天研究、森林防火与电力系统雷击定点等。LLS的主要组成部分为：省内探测站、中心站、通信系统与用户终端。基于不同的定位原理，LLS能够实时获得雷击点位置、方向等相关信息。因此，其成为雷电活动检测最主要的技术手段。LLS可分为二维平面与三维椭球面定位模型，针对LLS覆盖面积小以及地球曲率变化可忽略不计的情况，可采用二维平面定位模型。当在覆盖面积大或地球曲率变化影响较大的情况下，则需采用三维椭球定位模型。

LLS中所用到的定位算法可包括线性、非线性迭代定位算法与最优求解群智能算法。其中，针对线性定位算法，Koshak基于数学变换得到地球表面传播电磁波时的雷电定位算法[2]。基于时差定位，文献[3]提出线性化观测方程。但该线性化方程易受到地球曲率的影响而使得定位结果误差大。从而牛顿迭代、泰勒级数迭代与最小二乘法迭代等，非线性迭代算法相继被应用于雷击定位中。文献[4～6]均是基于时差原理，采用非线性方程组并进行迭代求得雷击定位信息的。但该类算法存在初值对算法收敛性影响大的缺点，故最优求解群智能算法被引入到雷击定位的求解当中。常用的解空间最优求解智能算法，有粒子群优化算法[7]、网格搜索法[8]等。其中，网格搜索法计算量大、稳定性弱。而粒子群优化算法虽计算量小，但易陷入局部最优解。综上，研究一种新的准确、稳定、有效的输电线雷击定位算法对克服以上算法缺点、及时定位雷电位置具有重要意义。

1.2 雷电定位系统探测原理

LLS定位系统的探测原理主要包括3种定位技术：时差定位、定向定位及综合时差与定向技术的定位[9]。

1)时差定位原理：首先计算雷电所发出的电磁波到达多个探测站的时间间隔，并将其与电磁波的波速相乘即可得到雷击位置。因环境影响电磁波的波速，加之时钟同步技术等原因。该定位原理误差大，且需要的探测站为3个及以上。

2)定向定位原理：基于球面三角形模型，建立两个探测站来寻求雷电方位。但由于探测站受环境影响大，而使得测量误差也相应较大。

3)时差与定向综合定位原理：该定位原理将时差定位原理与定向定位原理进行综合，赋予多个探测站一定的权值。最后，使用最小二乘法进行精确估计雷击位置。

综上所述，时差与定向综合定位原理误差最小，为1～3 km。其满足输电线雷击定位的精度要求，因而应用范围最广，是我国电网系统中主要采用的雷击定位方法。但雷电具有随机性，且地理环境、探测站分布与数据同步误差等因素严重影响着雷击定位精度。而在确定定位原理后，定位算法的选择对LLS定位系统检测精度而言至关重要。

2 果蝇优化算法框架

2.1 果蝇优化算法原理

仿照果蝇搜索食材的FOA寻找最优解具有计算量少、简单、易调节等优点[10-12]，且FOA通过随机初始化得到初始值。群体中果蝇是分布进行合作，某一果蝇的故障不会影响整体功能。因而FOA受初始值影响小，难以发散。果蝇搜索食物过程的依据为食物浓度[13-14]，当群体中的果蝇发现其他位置处的食物浓度更高时，便会飞过去。FOA具体步骤为：

1)设定种群规模Mpop，迭代次数最大值nmax，将果蝇群体坐标进行初始化：Xaxis，Yaxis；

2)由式(1)求果蝇个体坐标方程表示其方向与距离

(1)

3)分别由式(2)计算其离原点的距离Dist,i，并由式(3)计算味道浓度判定值ci：

(2)

ci=1/Dist,i

(3)

4)将式(3)求出的ci带入到味道浓度判定函数，来求得味道浓度csmell；

5)求果蝇群体味道浓度的极小值以及该位置处的果蝇

[csmell,best,cindex,best]=min(csmell,i)

(4)

6)求步骤(5)中果蝇的坐标并保留：

(5)

7)返回执行步骤5)，并与前一次迭代得到的味道浓度相比，判断所得到的味道浓度极小值是否减小。若是，则返回执行步骤6)；否则继续执行步骤(5)，直至达到最大迭代次数。

2.2 果蝇优化算法改进

FOA在求解过程中，常会因早熟收敛于局部最优解。故本文对其进行改进，将变步长与收敛因子引入其中。

2.2.1 变步长

传统固定步长的FOA会因步长设定过小而降低搜索效率，也会因步长过大而找不到最优解。因此，本文将变步长原理应用于FOA，每一步迭代能够自适应地选择步长，从而既提高搜索效率，也能快速找到最优解。式(6)为初始位置处果蝇的下一步随机位置计算式。式中，dL为搜索步长，(Xaxis,Yaxis)为初始坐标。

(6)

由式(7)味道浓度判定式，可得X(i)

(7)

(8)

从式(8)中可看出，1/ci为Xi的搜索数量级，ci为前一次迭代群体中味道浓度最优值。结合Yi，取步长为

(9)

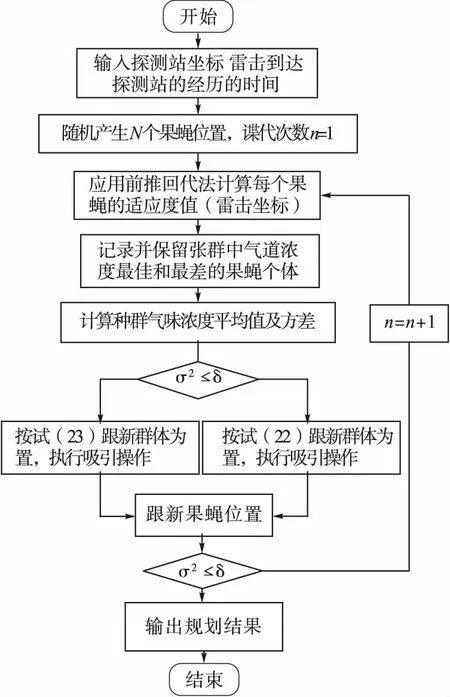
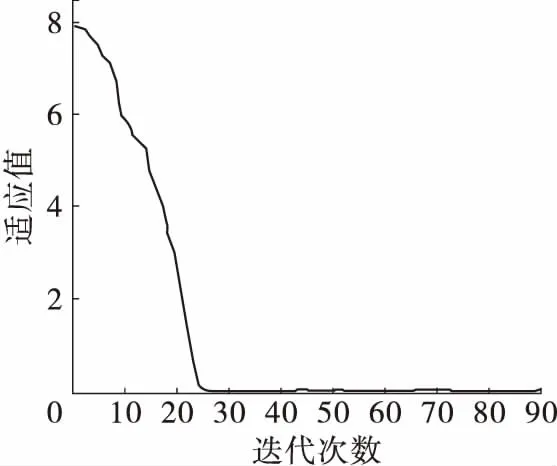
式中，h为常数，0.1

2.2.2 松弛因子

传统在二维搜索空间求解的FOA算法，在三维搜索空间中可能无法找到最优解。因此，本文引入松弛因子。Dist,i与ci均为正值，且其分别在大范围、小范围内搜索随机值，从而导致FOA步骤(4)早熟而陷入局部最优解。为解决该问题，将松弛因子引入味道浓度判定值ci的计算中，如式(10)所示。使得ci也可得到负值，脱离局部极值而找到全局极值。式中，k为随机值，区间为[0,1]，α为松弛因子。

ci=ci+α

(10)

α=(0.5-k)×Dist,i

(11)

3 基于MFOA的输电线雷击定位算法

3.1 雷电定位原理

由于地球是椭球面的，因而椭球面模型更为准确。设t时刻的雷击坐标为S(N，E)，N、E分别表示纬度与经度；探测站D的坐标为Di(Ni，Ei)，i=1，2，L，n，c=299 792 458 m/s为电磁波传播速度；则探测站观测到的雷电到达时间与方位，分别如式(12)和(13)所示。

(12)

φi=θip+ei

(13)

式中，探测站与雷电位置间的大地线长度与方位角表示为Lip、θip；时间与方位的误差表示为εi、ei。式(12)和式(13)的求解需要在三维空间中进行。

式(14)为味道浓度判定函数式，其是雷击点与各探测站位置的误差之和，也即果蝇位置与原点最小距离。由于误差可能为负数，故式(14)中取误差的平方进行计算。

ci=f(Dist，i2)

(14)

果蝇与原点间的距离，也即探测站与雷击点距离误差表示为

Dist,i=|cεi|=|cti-ct0-Lip|

(15)

式中，t0为探测站计算的雷电发生时间平均值，表示为式(16)。式(17)和式(18)分别为时间差定位、时间差与定向综合定位的适应度函数。

(16)

(17)

(18)

按式(19)记录最佳和最差味道浓度值及其位置。

(19)

式中，(Xb,Yb)为最佳味道浓度值csmell,best时的位置；(Xw,Yw)为最差味道浓度值csmell,worst时的位置。按照式(20)和式(21)计算种群气味浓度的平均值csmell,avg和方差σ2。

(20)

(21)

给定方差阈值δ，若σ2≤δ，则执行排斥操作，按式(22)更新群体位置；反之，执行吸引操作，根据式(23)更新群体位置。

(22)

(23)

3.2 参数求解

椭球面上的大地主题反算，是由经纬度计算两点间的大地线长度与方位角。文献[15]中系统总结了如仅适用于短距离的高斯平均引数法、受距离限制的高斯投影法、计算量大的数值分析法等大地主题反算方法。而大地主题反算法中的贝塞尔法求解精度与距离无关，且距离可达到10 m。因此，本文采用该算法进行大地主题反算，文献[16]为其求解过程。

本文所设计的基于MFOA输电线雷击定位算法流程图，如图1所示。

图1 基于MFOA输电线雷击定位算法流程图Fig.1 Flow chart of lightning strike location algorithm based on MFOA

4 仿真分析

某地区发生雷击时，各探测站位置与其所探测到的雷击时间，如表1所示。

表1 探测站坐标及其探测的雷击发生时间Table 1 Probe Station Coordinates and Detection of Lightning Strike Occurrence Time

基于MFOA在椭球体上对雷击进行定位。其中，果蝇种群数目为50，迭代次数为90。算法的适应度值随迭代次数的变化，如图2所示。首先根据六个探测点与雷击点的距离估算出雷击坐标为(35°36′28.421″,113°27′25.236″)，其作为果绳群体的初始坐标(X_axis，Y_axis)，通过式(1)产生初代果蝇种群(X1，Y1)，(X2，Y2)，…，(X50，Y50)，并计算每个果蝇气味浓度，记录下最佳味道浓度值时的果蝇的位置作为下一代果蝇种群的初始位置，通过式(9)计算可变迭代步长，并更新下一代种群。重复以上步骤直至达到最高迭代次数(在本文中最高迭代次数为90)，此时最佳味道浓度值时果蝇的位置则为最优解。由该算法最终得到雷击坐标为(36°25′19.348″，111°81′14.165″)，实际雷击坐标为(36°25′13.79″，111°80′60.79″)。两者之间的误差为401.125 m，满足定位精度，从而验证了本文所提出的基于MFOA的输电线雷击定位算法的可行性。且由图2中可得到，该算法能够从局部最优解跳出，最终收敛到全局最优解。通过后期大量仿真验证，该算法一般迭代次数为25～90次即可求得全局最优解。辅助于计算机，其收敛速度将大幅提高。

图2 基于MFOA雷电定位计算的迭代过程Fig.2 Iterative process of lightning location calculation based on MFOA

5 结语

针对传统雷击定位方法因易受初始值的影响而结果发散的问题，提出一种基于MFOA的输电线雷击定位算法。将FOA引入雷击定位中，并对其进行步长可调与增加松弛因子的改进，使其难以陷入局部最优解。同时，通过不断缩小探测点与雷击点距离的误差来最终获得雷击位置。最后对所提的算法进行仿真验证，证明了其能够准确、及时地定位雷击位置，具有误差小、计算速度快的优点。