吊缆失效时悬索桥整体稳定性的数值分析

彭玉林 樊 源

(陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007)

0 引言

悬索桥作为千米级以上跨度的首选桥型[1]，被破坏后所带来的影响大，成为恐怖主义和敌对势力打击的重要目标。因此对悬索桥在爆炸袭击下的整体稳定性研究显得极为重要。

目前，桥梁的抗爆研究还处在初级阶段。Shukla[2]研究了斜拉桥桥墩在比例距离爆炸袭击下的响应；Marchand[3]的研究指出在桥墩处爆炸时，桥墩和桥面组合构成的密闭环境对爆炸冲击波有增强效果；Tang和Hao[4,5]利用LS-DYNA建立了斜拉桥的三维有限元模型，通过有限元方法模拟了斜拉桥不同位置受到爆炸荷载作用的动力响应；由于利用大型有限元分析程序，如ANSYS和LS-DYNA，进行结构爆炸性能研究具有模型复杂、计算困难、影响因素多等问题。Mahoney[6]利用较为简便的SAP2000有限元程序研究了不同桥型在爆炸作用下的响应，分析了各桥型在不同爆炸工况下造成的损失。在桥梁抗爆设计研究中，国内外学者主要参照桥梁结构的抗震设计。而Suthar[7]指出地震荷载下桥墩的变形为水平方向反复振动，而爆炸荷载下桥墩发生局部破坏。因此桥梁抗爆设计并不能完全借鉴抗震设计。

本文以润扬长江大桥南汊悬索段(简称润扬大桥)为例，基于SAP2000建立了润扬大桥二维简化模型，并讨论其吊缆遭受爆炸袭击的整体稳定性。

1 模型建立与验证

根据文献[8]，在只考虑桥梁二维竖弯情况下，可采用如图1所示的二维简化模型，桥梁尺寸及构造见文献[9]，主索、吊缆均采用强度为1 670 MPa的镀锌高强钢丝，加劲梁材料为Q345D钢材，箱梁形式按矩形截面简化，顶板和腹板厚14 mm，底板厚10 mm。部分参数如表1所示，邻塔的吊缆与塔间距为20.5 m。各单元材料属性及截面如表2所示。

该桥具有2根主索，2排吊缆，将二维模型中的主索和吊缆按照2倍截面建立，吊缆截面较小，自重相对而言较小故忽略不计。索缆和加劲梁均采用Frame单元，主索和加劲梁按照索距划分为92个单元。主索和吊缆单元端部选择释放两端弯矩和一端扭矩，每跨加劲梁间为刚接。

润扬大桥主跨跨径长达1 490 m，在分析中需要使用挠度理论，计入荷载内力对悬索桥刚度的贡献[10]，在SAP2000中选择非线性、P—Δ分析功能。在主缆和加劲梁自重荷载下结构受力情况见表3，通过与文献[8]对比，结果相差不大。在SAP2000中在索缆上设置初始负应变以抵消结构自重产生的变形。索缆初始应变按照单元上最小轴力保守计算，主索和吊缆初应变分别为：-2.65×10-3和-8.97×10-5。得到最终静挠度见表3，对于千米级跨度，在可接受范围内。表4是利用SAP2000中的模态分析，得到的低阶结构自振频率，其结果与文献[8]的对比误差在10%以内。综上，可验证SAP2000中所建模型的有效性。

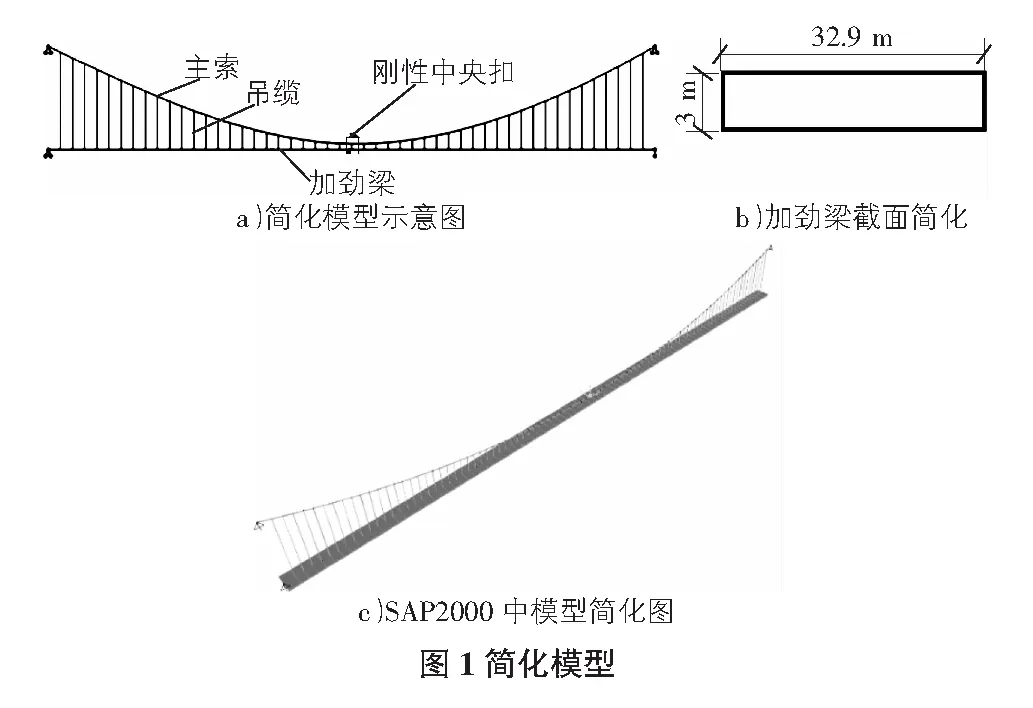
表1 桥梁主要参数 m

表2 材料主要参数

表3 恒载下桥梁内力

表4 桥梁自振频率 Hz

2 吊缆拆除后桥梁稳定性研究

由于吊缆截面尺寸较小，爆炸袭击时锚固位置容易失效。且在桥梁使用过程中，吊缆是一个容易接近且容易破坏的部位，因此考虑在爆炸荷载下吊缆失效后桥梁的整体稳定性。为模拟悬索桥部分吊缆被暴恐分子或敌人炸断，采用拆除法即假定受到袭击时其余构件不受影响单独移除部分吊缆，探讨桥梁受力性能。

2.1 吊缆移除后的内力计算

在SAP2000中，当移除跨中一根吊缆(刚性中央扣旁吊缆)时：相邻两侧吊缆内力变大，但由于吊缆初始内力小且移除后的增幅不大，其内力仍在可承受范围内；相邻两侧梁上弯矩增大，跨中吊杆节点处由负弯矩变为正弯矩且数值增大，但仍在承载力范围之内。

依次将1号～10号吊缆移除，见图2随着吊缆移除数目增加，失效中心处弯矩将明显增加，当10根吊缆全部移除时，加劲梁上弯矩接近极限承载力，即将破坏。表5为移除1根,3根,5根,7根,10根吊缆时，加劲梁最大弯矩及相邻两侧吊缆拉力。

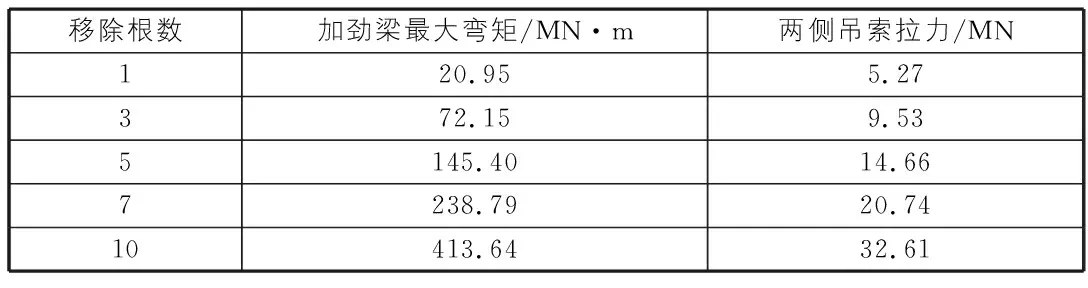
表5 吊缆移除后内力

根据钢梁截面弯曲正应力公式计算加劲梁的抗弯承载力，中性轴位置y按0.5倍梁高估算。

Mb=[σ]bIy/y=429.80 MN·m

(1)

其中，Mb为梁截面抗弯承载力；y为中性轴距梁底高度；Iy为梁截面惯性矩；[σ]b为梁截面材料的容许正应力，Q345D钢材容许正应力取310 MPa。

根据吊缆承载力验算公式，考虑安全系数Ks=4，计算吊缆的极限拉力。

Ts=[σ]sAs/Ks=66.38 MN

(2)

其中，Ts为吊缆的极限拉力；As为吊缆截面面积；Ks为安全系数；[σ]s为吊缆截面材料的容许应力，取值为1 670 MPa。

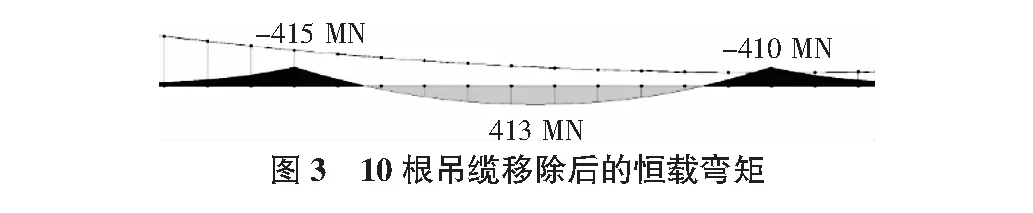
因此，吊缆的安全储备更高。在暴恐袭击过程中，若部分吊缆受到攻击而失效，加劲梁会在恒载作用下抗弯承载力达到极限而发生破坏，而其余吊缆不会由于恒载作用发生连续性破坏。因此，对于该桥而言，若有连续的10根吊缆被破坏，则该桥在自重作用下加劲梁最大弯矩接近极限承载力。显然，当超过连续10根吊缆被破坏，加劲梁将发生弯曲破坏。图3为加劲梁在10根吊缆失效情况下的弯矩图，其吊缆失效段的中间部位弯矩最大，相邻两侧吊缆处出现较大负弯矩。

根据表6结构在10根吊缆移除后自振频率与原结构相比，发现结构自振频率变化不大。说明对于如此大型的悬索桥结构而言，局部吊缆的失效对于桥梁整体结构动力特性影响不大。

表6 吊杆移除后与原结构自振频率的比较

2.2 吊缆移除后的连续破坏分析

从悬索桥荷载传递路径来看，桥面荷载通过吊缆传递给主索再由主索传递给桥塔与基础，主索和吊缆在桥梁传力中具有极重要的作用。当数根吊缆在爆炸袭击时发生断裂，其所受荷载将分配到两侧吊缆上，由此可能导致两侧吊缆由于承载力不足而拉断，从而导致所有吊缆连续破坏。2.1节的内力计算表明吊缆承载力高，加劲梁弯曲承载力弱，但加劲梁受弯破坏为延性破坏，而吊缆的拉断更趋于脆性破坏，因此当加劲梁还未完成受弯破坏过程时，而两侧剩余吊缆可能会先被拉断。因此对于吊缆失效后两侧吊缆的连续破坏研究具有一定意义。

假定本文所述润扬大桥加劲梁承载力足够高，考虑仅在桥梁恒载作用下，基于2.1节所得到的吊缆承载力，计算出要发生连续倒塌所需要移除的最小吊缆根数为2Ts/(gl)-1=40根，其中，g，l分别为加劲梁每延米自重和相邻吊缆间距。因此可知，若想使得润扬大桥发生吊缆连续拉裂破坏，需要将相邻的40根吊缆同时破坏。这种条件极为苛刻，现实中基本不可能发生。但对于某些设计不合理、或是吊缆安全储备不高甚至没有储备的桥梁中，吊缆连续破坏问题值得注意。

3 结语

本文基于SAP2000有限元软件，建立了润扬大桥的二维有限元简化模型，并讨论了该桥在逐次拆除吊缆后的整体稳定性，计算结果表明，10根吊缆失效后，润扬大桥局部加劲梁达到承载能力极限；相邻的40根吊缆同时拆除后，其剩余吊缆在自重作用下连续拉裂破坏，桥梁失稳倒塌破坏。本文提供悬索桥的建模方法以及其整体稳定性检验的详细过程，为结构的防灾减灾和预测检验提供一定的经验和方法。