结合矩阵分解和延伸相似度的最近邻算法

李俭兵，刘栗材

(1.重庆邮电大学 通信新技术应用研究中心，重庆 400065；2.重庆信科设计有限公司，重庆 400021)

0 引 言

传统推荐系统[1,2]主要有协同过滤推荐、基于内容的推荐、混合推荐[3]。协同过滤算法在推荐领域为最基本推荐算法。传统的协同过滤推荐算法可以分为基于用户的协同过滤和基于产品的协同过滤[4]。目前在协同过滤推荐模型中使用得最广泛的算法是最近邻方法[5,6]。然而最近邻方法有数据稀疏、个性化低和计算负荷量大等特点[7]，大大降低个性化推荐准确性。最近邻算法计算的对象是高维矩阵，需要大量的运算时间且精确度低。文献[3]中提出用一种聚类算法优化K近邻协同过滤算法来提高精确度。文献[8]利用矩阵分解技术和KNN算法提出了扩展滤波算法，简化了矩阵，增强用户影响力。当然在推荐系统中，相似度也非常重要[9]。文献[10]中提出一种基于加权双边网络和协同过滤的资源分配原则来计算用户相似度，从而提高推荐准确度。

针对最近邻算法依赖完全匹配，导致算法牺牲推荐系统的覆盖率和准确度。本文在KNN算法基础上提出了结合降维的最近邻算法(K nearest neighbor algorithm of dimensionality reduction，KNN-DR)来有效解决计算式复杂度高和推荐效果大众化的特点。实验结果表明，KNN-DR算法与KNN算法相比可以更好地实现精确预测。

1 相关问题和工作

1.1 相关问题

本文以电影推荐网站为例，网站的用户行为有数据复杂，需求多样性等特点。在不知道具体的影片名的情况上，电影推荐网站传统的推荐方法有如下几种：第一种是通过用户检索出关键字，网站给出这系列所有电影名，然后用户查询自己喜欢的电影；第二种针对所有的用户都推荐同一个热门排行榜；另外一种是根据用户观影记录，推荐之前观看的类似影片。

以上的推荐算法虽然取得不错的效果，但是效率低和个性化效果差。本文先用矩阵分解的方法降维,加快运算效率。然后用相似度法将最近的邻里的数据进行加权计算。本文不仅考虑了运算速度，且融合了更多隐式因子，使个性化推荐更加精准。根据KNN-DR方法形成用户邻里关系如图1如示。

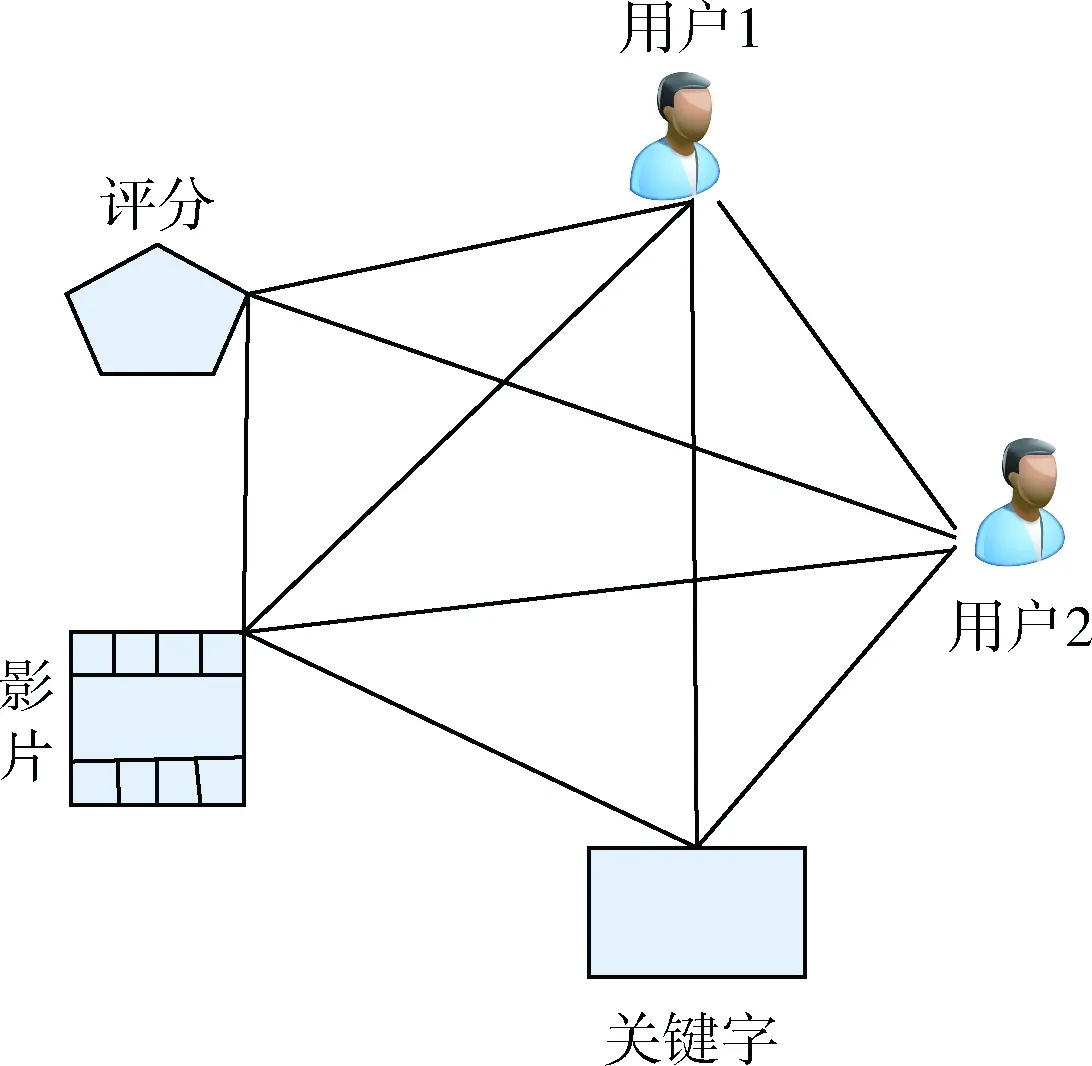
图1 用户邻里关系

1.2 相似性度量值

(1)皮尔逊相似度

协方差的概念反映出两个随机变量的相关程度，如果两个变量同时变大或者变小，就说明这两个变量的协方差为正数,相反为负数

(1)

式中：ρ(x,y)表示皮尔逊相关系数，分子为x和y的协方差，分母为x的标准差乘以y的标准差。μx和μy分别是用户x和y评分的平均值。皮尔逊相关系数其实在几何上可理解为夹角的余弦值。

(2)延伸相似度

用户间差异对推荐也很重要,反映了电影推荐系统的质量。针对同一部电影，在计算用户间差异值的时候，引入了评分相对值，尽可能降低由于喜好风格不同，使评分相差太大[11,12]。用户可以从1到5的5个整数中选择相应的分数表达对影片的喜爱程度。我们从数据集中可以看出，同一部电影,不同用户给出的评分差距太悬殊。所以有式(2)

(2)

当用户x的评分Gx和用户y的Gy不相等时使用上式，当Gx和Gy相等时，M(x,y)等于1。相对值M(x,y)的范围在[0.25,1]。在用户间评分差值达到最大的4时(M为0.25)，认为相对值最低；评分差值达到1时(M为1)，相对值最高。因此，在这范围内越大，相对值越高。不同用户喜欢不同风格的影片，为了计算他们间的相同观影风格，引入了相同性概念

(3)

式中：MS(x,y)表示用户x和y的相同性。w(·)表示用户观看的影片。为了使指标分布在(0,1)上，上式进行了变化。公式如式(4)

(4)

把用户间的这些隐式关系引入进推荐系统中,使评分相对值和CMS(x,y)相加再与皮尔逊相似度结合，得出了用户间的延伸相似度[13]

RS(x,y)=(M(x,y)+CMS(x,y))ρ(x,y)

(5)

在时间跨度比较大的情况下，时间可能改变兴趣

(6)

又

(7)

sim(i,j)为产品的相似度，|N(·)|为喜欢产品i或j的用户数，N(j)∩N(i)是同时喜欢产品i和j的用户数，t(xj)是用户x对物品j观看的时间，t(0)是用户x观看物品j时距离当前时间最近的一次，β是时间衰减参数，需要根据不同的数据集选择合适的值。P(x,j)表示用户x对产品j的兴趣。最后通过加权计算得出[14]

(8)

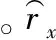
2 KNN-DR算法流程

在大数据时代，我们可以获得大量的数据，但是大部分都是冗余数据。融合了KNN协同过滤和矩阵分解技术。在运算时降低搭建的特征空间维度，提高运行效率和解决数据稀疏性。KNN-DR算法在传统推荐算法上把多种隐式信息融合进模型，进一步提高推荐精度，形成了具有针对性的个性化推荐。

2.1 KNN协同过滤

KNN的主要思路是如果一个样本在特征空间中的k个最相似样本中大多数属于某一个类别,则该样本也属于这个样本。大多数基于协同过滤的推荐系统,通过选取相似度高的k个邻居。根据它们来预测某一用户对某产品的评分分数。表达式如下

(9)

2.2 多特征融合型矩阵分解

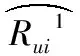
又考虑网站给出用户对影片的评分值，所以在构造函数时需要增加几项

(10)

μ是整个训练中全局评分均值，bi表示影片评分平均值，bu表示用户u评分相对均值u的偏见值。

(11)

给用户推荐主题，推荐系统会给出很多关键词，通常用户对排名靠前的更加关注。影片名里面包括了很多关键字，每一个关键字对应一个(term frequency-inverse document frequency，TF-IDF)权重，关键字是对用户自己的个性或兴趣做出的描述[15]。对于影片名关键词提取，由于影片名很短，使用TF-IDF存在稀疏性较大的问题。为了提高推荐的准确率，在上面的基础上再对提取的标签集进行扩展，把一个标签的相似标签加入这一集合中。通过相似度计算公式计算各个标签的相似度，选取相关的标签为一个集合。这样就解决了稀疏性。然后将这些标签集里分别进行聚合排序，将排序结果中前面的标签作为某同一类型电影,推荐给用户

(12)

K(·)为用户u的关键字，W(·,m)表示关键字m的权重，数值越大，表示u和m的相关度越高。y(m)为文档总数与词m所出现文件数比值的对数值。

所以，真实值和预测值的总误差平方和为

(13)

为了防止过拟合，对M进行正则化，添加处罚项，得

(14)

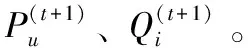
2.3 优 化

通过以上的分解，可以分别得到P、Q矩阵。根据基矩阵P，计算得到目标用户评分向量G对基矩阵P的投影向量q。再计算出投影向量q与投影矩阵Q各行间的欧氏距离，并对其设定一个阈值，将其中距离最小的前k个用户组成与目标用户的最近的邻里集合。通过这种投影的方式，在损失一些精度情况下可以加快计算速度

(15)

dist(·)表示欧式距离。在欧式距离计算中，取值范围会很大，一般通过如下方式归一化

(16)

最后再用上文提到的Px,j将最近集合中的数据进行加权计算，然后排序进行推荐。

2.4 时间复杂度

在KNN训练中计算复杂度与训练集中的数据为正比，所以时间复杂度为O(n*m)，n为训练数据集的大小，m为维数[16]。KNN算法每次要计算目标用户与其它用户的距离，所以增加了训练的时间复杂度。但是在KNN-DR算法中，可以通过对高维数据进行降维，减小空间特征维数，从而提高计算速度。假设原始训练数据集中有n个m维向量，对k个m维向量进行分类。则传统的KNN算法时间复杂度为O(k*m*n+k*n*lg(n))，但是KNN-DR为O(k*m*n1+k*n1*lg(n1)+n*lg(n)+m*n)，n1是通过多特征型矩阵分解得到的，其值小于原始训练集中n，所以传统的KNN模型时间复杂度大于KNN-DR模型。

3 实验分析和仿真

本文首先将已有的算法和本文研究的算法对比，结合查全率和准确率进行效果比较。

3.1 数据集

本文数据集是来自Netflix(http://data-ju.cn/Dataju/web/datasetInstanceDetail/116)。文件“Train-set.ar”包含17 770个文件，分别代表顺序为1到17770的MovieID。每一个MovieID后面跟着观看且评分的客户ID，等级[1,5]，评价日期。文件“movie-titles.txt”，格式如下：Mo-vie-ID，Year of Release，标题。Year of Release对应发行日期，从1890到2005。标题是Netflix的电影标题。

3.2 推荐评定指标

3.2.1 RMSE评估准则

RMSE全称为root-mean-square-error，均方根误差。它是观测值与真值的偏差的平方和观测次数n比值的平方根。均方根误差能很好反映出精密度

(17)

xobs,i表示用户对产品i的真实评分，xmodel,i为用户对i的预测评分。下面比较文中提到的几种算法。横轴train ration, X为选取的训练集大小与整个数据集大小的比值,如图2所示。

图2 RMSE和覆盖率的变化(影片数据)

train ration, X为选取的训练集大小与整个数据集的比值。部分算法出现相近的结果，所以一些研究人员提出了算法的准确性存在限制。这个限制将与用户的兴趣变化有关。鉴于一个人在不同场合对某个产品的意见可以每次都能给出不同的评分，所以算法的预测总是会受到这个影响。虽然不否认这个限制的存在，但在本实验3种算法结果相比之下，算法所遭受的最大限制是缺乏信息。预测的准确性受到从评分矩阵(影片数据里含大量评分信息)可以获得的信息量限制。而这进一步受到矩阵中实际存在的信息(特征)的限制。其实如前所述,训练集中的评分比例越大(信息量的增加)，结果就会改善。实验结果表明，过程中融合了更多隐式因子来增强个性化的KNN-DR算法在实验中比其它算法效果好。

3.2.2 F1评定指标

为了评估top-N推荐系统效果，经常使用的两个指标是召回率(recall)和准确率(precision)

(18)

(19)

然而，这两个指标经常矛盾。增加N值，召回率增加，但是准确率降低。实际中，使用F1值作为指标平均值，表达式如式(20)

(20)

第二个实验选取KNN的高维度处理模型与KNN-DR算法的低维度模型进行效果对比。首先选取合适的X值。需要注意的是，X的取值不同是用于确定不同模型对训练集稀疏度的敏感度。

运行KNN和KNN-DR情况下实验，随着不同的X值，计算出F1度量值。图3横轴代表X，纵轴代表F1值。通过图3的实验结果，可以得出电影数据的最佳X值是取0.8。

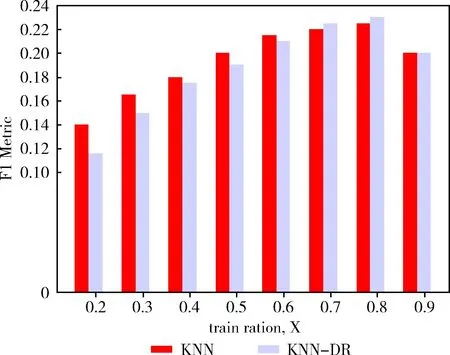
图3 最优X的值确定(影片数据)

我们通过算法得出top-N，N为10。且通过上面图表确定了X为0.8时可以使推荐效果达到最佳。把KNN的高维度模型与KNN-DR算法的低维度模型进行对比。

图4的横轴表示维度的数量，纵轴表示F1值。通过实验结果表明，KNN-DR算法在KNN的基础上推荐效果有了明显的提高。

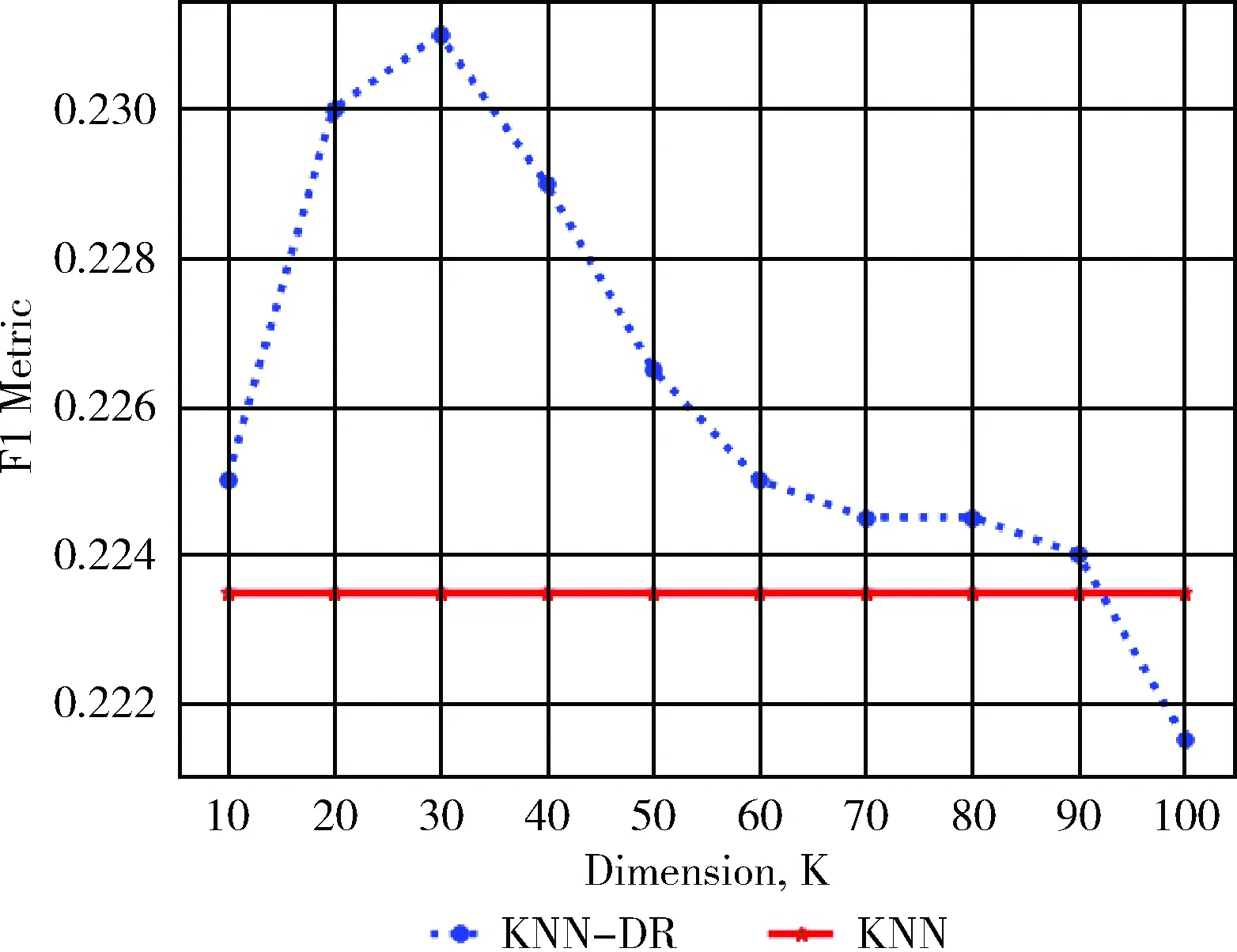
图4 Top-10推荐结果(影片数据)

图5的实验选取了训练集大小与整个数据集的比值分别为0.5，0.6，0.7，0.8，0.9进行对比训练时间。随着训练数据的增加，时间差也逐渐增加，说明KNN-DR算法通过降维的方法对运算速度有提高。

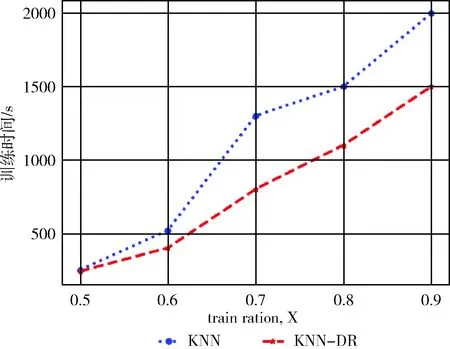
图5 两种算法训练时间对比

4 结束语

本文以电影网站中推荐系统为背景，将传统的KNN算法与矩阵分解相结合，提出了KNN-DR算法。与传统的KNN算法相比，KNN-DR算法通过降维的方法加快了运算速度，然后在低维空间形成邻里，专注分析给定邻里用户喜欢的产品。并且这种算法包含了对隐式因子的考虑，通过延伸相似度和皮尔逊相似度来加权计算得出相似度计算式，最后再排序推荐，提高推荐精确度。实验结果表明了这种算法的可行性和有效性。在不同的评分推荐系统背景下，我们可以替换计算式中的权重和关系系数的大小，来实现个性化推荐。在这里，我们学习潜在特征向量的同时考虑用从数据中学习的任意函数替换内积。目前有很多高效的算法,如神经网络算法、GBDT(gradient boosting decision tree)等。如何利用神经网络来代替上文用户邻里关系网，通过优化固定网络的潜在特征来学习，是未来要研究的课题之一。