基于共轭梯度的EKF姿态估计算法
2018-10-24曾聪,章政,2,王龙
曾 聪,章 政,2,王 龙
(1.武汉科技大学 信息科学与工程学院, 湖北 武汉 430081;2.武汉科技大学 冶金自动化与检测技术教育部工程研究中心, 湖北 武汉 430081; 3.湖北汽车工业学院 电气与信息工程学院, 湖北 十堰 442000)
0 引 言
姿态解算是四旋翼飞行器[1-3]设计的核心环节,由于微机电系统(micro-electro mechanical systems,MEMS)具有成本低、体积小、功耗低等特点,它已成为了四旋翼姿态测量的首选器件[4]。但是实际的导航问题中,低成本的陀螺仪存在漂移,长时间运行漂移严重会产生累积误差,易导致解算姿态不稳定[5],因此实现多传感器融合及设计稳定快速的滤波算法是获取飞行器精准的姿态信息的有效途径之一[6]。
文献[7]和文献[8]提出了一种基于互补滤波的姿态解算算法,该算法利用加速度计和磁力计来补偿陀螺仪漂移所引起的姿态偏差。文献[9]和文献[10]提出了一种基于梯度下降法的姿态融合算法,利用梯度下降法求解出目标函数误差方程姿态四元数与微分方程求解出的姿态四元数进行融合,得到最优姿态。由于互补滤波和梯度算法均没有对系统过程噪声和传感器的观测噪声进行分析,从理论上已证明Kalman滤波算法是不同导航器件的测量信息和系统状态信息融合的有效方法。文献[11]采用了基于四元数的卡尔曼(Kalman filter,KF)滤波器姿态估计算法,将过程噪声和观测噪声引入姿态估计系统,通过KF滤波器进行姿态融合,但是KF滤波器针对的是线性系统,而飞行器姿态估计系统一般是非线性系统。文献[12]提出了一种扩展卡尔曼滤波(extended Kalman filter,EKF)算法,该算法把非线性系统进行线性化,提高了姿态估计的精度,但是在观测方程线性化的同时引入了线性误差。文献[13]将EKF姿态估计算法进行改进,该改进算法将梯度下降法所得到的姿态四元数引入观测量,很好地解决了观测模型线性化的误差。文献[14]提出了一种无迹卡尔曼滤波(unscented Kalman filter,UKF)姿态估计算法,该算法有效解决了上述观测模型的线性误差,同时也提高了姿态估计的精度。文献[15]提出了一种基于粒子滤波(particle filter,PF)的飞行器姿态估计算法,该算法将状态向量分为线性部分和非线性部分分别进行处理,有效地提高了姿态估计的精度和稳定性。然而,在实际应用过程中,UKF算法和PF算法计算量过大,实现过程相对比较复杂,不易在MEMS中实现。
针对MEMS中单个惯性测量器件可信度低和复杂算法对硬件要求高等问题,本文提出一种基于共轭梯度的扩展卡尔曼姿态估计算法。该算法通过将共轭梯度引入观测模型,对噪声进行动态的估计并采用倾角补偿的方法单独计算偏航角从而提高了飞行器姿态解算的精度和抗干扰性能。本文设计4组对比实验,实验数据表明改进EFK算法能够快速可靠跟踪飞行器的姿态,并实现自主悬停。
1 四元数姿态系统
1.1 坐标系介绍
在姿态解算中,通常定义两个坐标系表达姿态角的关系,分别为导航坐标系(n系)和机体坐标系(b系),如图1所示。导航坐标系使用东北天(ENU)坐标系,机体坐标系使用标准右前上坐标系,导航坐标系与机体坐标系原点重合且位于机体质心。通常定义绕x轴旋转的姿态角为倾仰角(pitch)、绕y轴旋转的姿态角为横滚角(roll)、绕z轴旋转的姿态角为偏航角(yaw),分别对应图中的Φ、θ、Ψ。

图1 坐标系旋转
1.2 四元数与姿态的转换
通常使用四元数法、欧拉角法、方向余弦法[7]描述导航坐标系与机体坐标系的转换关系。其中欧拉角法会遇到Gimbal Lock问题,方向余弦法计算量大、效率低无法满足四旋翼飞行器的姿态解算,本文采用简单易行、效率高的四元数法进行姿态解算。

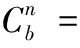
(1)
根据zyx顺规Φ、θ、Ψ,有如下转换公式
(2)
1.3 四元数更新算法
姿态解算使用四元数微分方程完成姿态四元数更新。四元数微分方程表述的是角速度与四元数的关系,如式(3)所示
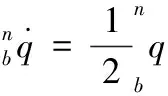
(3)
采用离散迭代的方法更新四元数,由式(4)可得
(4)
2 改进EKF姿态估计算法
由于常规的EKF算法在精度和抗干扰性方面还存在不足,本文提出一种基于共轭梯度的扩展卡尔曼姿态估计算法,该算法结构如图2所示。
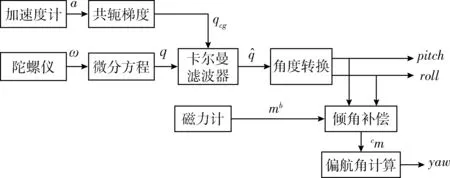
图2 基于共轭梯度的扩展卡尔曼姿态估计算法结构
2.1 卡尔曼滤波器的设计
2.1.1 状态模型
本文所设计的状态模型选取姿态四元数作为状态量,根据式(3)中的四元数微分方程可以得到如下系统状态方程
(5)
式中:Ω[ωb]是一个4*4的反对称矩阵,如式(6)
(6)
对式(5)进行离散化处理,假设陀螺仪的采样周期为Ts(至少20 ms),经过离散化的状态方程如式(7)
(7)
陀螺仪的输出量作为状态转移的变量,陀螺仪的模型如式(8)所示[16]
ω=ωr+gb+gω
(8)
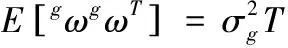
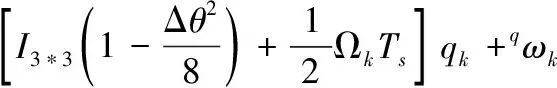
(9)
(10)

(11)
2.1.2 观测模型
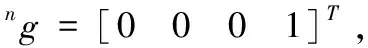
构造目标误差方程,如式(12)所示
(12)
根据共轭梯度法[17],可按照式(13)更新机体姿态四元数
qcg,k+1=qcg,k+λkdk
(13)
式中:λk为第k次姿态跟新的最优步长,dk为第k次姿态更新的搜索方向,qcg,k为第k次更新的姿态四元数。
根据文献[17]中共轭梯度法,姿态计算过程如式(14)所示
(14)
(15)
J(q)为式(15)的雅克比矩阵
(16)
通过以上公式计算过程,不停的进行姿态四元数的迭代更新,并作为卡尔曼滤波器的观测量。使得观测模型可以简化为
Zk=qcg,k-1=xk+vk,k=1,2,3,…
(17)
式中:qcg,k为共轭梯度法计算出来的卡尔曼的观测量,观测模型的噪声与加速度的测量噪声vk相关。所以过程噪声协方差矩阵如式(18)所示
(18)
由此可得,观测模型的观测矩阵Hk=I4*4。根据卡尔曼滤波器的黄金五步法[13],基于共轭梯度的卡尔曼姿态估计算法如图3所示。
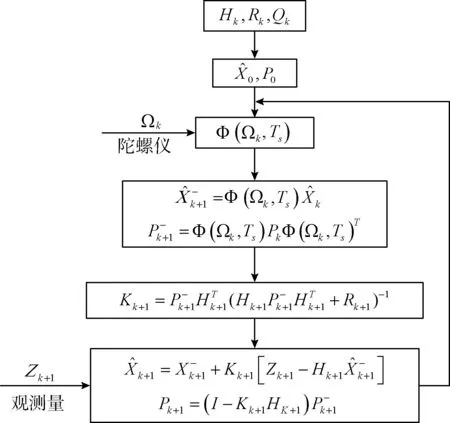
图3 基于共轭梯度的扩展卡尔曼姿态估计算法步骤
2.2 变噪声处理
在实际飞行运动过程中,四旋翼飞行器一般都是非匀速飞行,飞行器在高速飞行时会产生一定的运动加速度,这种运动加速度会降低姿态估计的精度,对姿态的控制产生不利的影响。通过常规物理减震方法和卡尔曼滤波器对高频震动具有良好的滤波效果,但是无法消除非重力运动加速度的影响。这种非重力运动加速度是一种非零随机噪声,在观测模型中,一般假设式(18)中的观测噪声Rk为常量,这样会降低姿态估计的精度。针对上述非重力运动加速度对姿态估计造成的影响,本文根据环境的变化设计一种自适应处理方法,该方法将观测噪声视为一种随非重力运动加速度实时变化的动态随机噪声,从而实现噪声的动态跟踪估计。
假设在非重力运动加速度可忽略的情况下,测得过程噪声的协方差矩阵最优值为R0,设计k时刻的观测噪声协方差矩阵如式(19)所示
Rk=αR0
(19)
式中:α为观测噪声的自适应调整因子,当非重力运动加速度越大时,Rk也越大
(20)
式中:μ为可调参数,为常量,根据实际情况和不同的系统做适当的调整即可。
2.3 改进偏航角估计
在实际飞行的环境中,存在一些磁干扰源的影响,造成磁力计的测量值会产生很大的误差,导致水平姿态解算错误。为了避免磁干扰造成的水平姿态解算误差,在改进的EKF算法中,未将磁力计的测量值融合到卡尔曼滤波器中,而是单独的计算偏航角,由此增强了姿态的抗磁干扰能力。

(21)
式中:pitch(Φ)和roll(θ)由式(2)中给出,偏航角yaw(Ψ)由倾角补偿后磁力计计算可得
(22)
3 实验研究
3.1 实验平台
本实验平台采用自行设计的飞控板实现,选用STM32F405(Cortex-M4内核)为主控处理器,最高工作频率可达168 MHz。IMU采用MPU6050和MS5611,MPU6050集成一个三轴加速度计和一个陀螺仪,MS5611用于测量磁场。系统的控制频率为250 Hz,即4 ms进行一次姿态解算。
四旋翼飞行器的各项数据见表1。
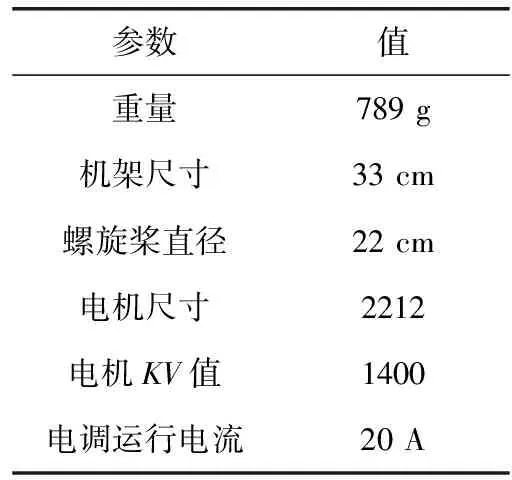
表1 四旋翼飞行器各项数据
3.2 实验与结果分析
为了验证本文所设计算法的可行性和有效性,本文设计了4组对比实验:第一组实验为静态对比实验,验证算法的静态性能。第二组实验为磁干扰对比实验,验证算法的抗磁性能。第三组实验为水平滑动对比实验,验证算法在非重力运动加速度干扰下,姿态解算的准确性。第四组实验为绕轴转动对比实验,验证算法的动态性能。
3.2.1 静态实验
静态实验将四旋翼飞行器放置在无磁干扰水平的平台上,分别采集两组算法的姿态角进行对比。根据图4可以得到各算法姿态角的标准差和波动范围见表2。两种姿态估计算法基本满足四旋翼飞行器飞行要求,在静态时改进的EKF姿态估计算法的波动范围和标准差小于常规的EKF姿态估计算法。由该组静态实验对比可知,改进的EKF姿态估计算法比常规的EKF姿态估计算法精度更高,解算的姿态更加稳定。
3.2.2 磁干扰实验
磁实验将四旋翼飞行器静止放置在一个无磁干扰源的水平平台上,利用一根有电流流过的导线模拟磁场干扰源,在四旋翼飞行器的上方来回划动。两种算法的磁干扰实验结果如图5所示。在干扰磁场加入后,常规EKF姿态估计算法的水平姿态角pitch和roll角受到磁干扰影响严重,而改进EKF姿态估计算法几乎不受磁干扰的影响。由抗磁实验对比可知,从卡尔曼滤波器中分离出偏航角的改进EKF姿态估计算法的抗磁能力明显增强。
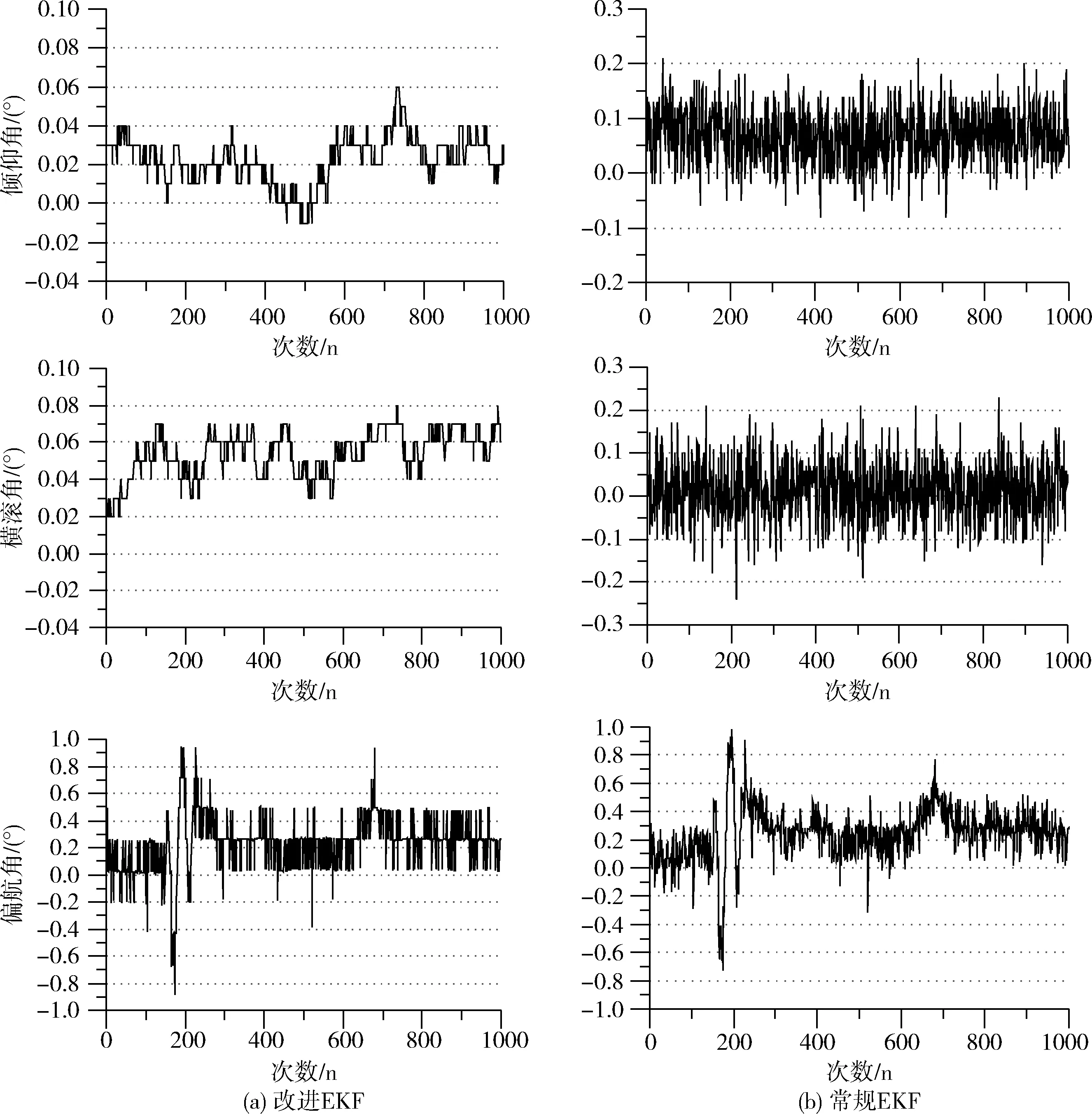
图4 静态实验两种算法的姿态角
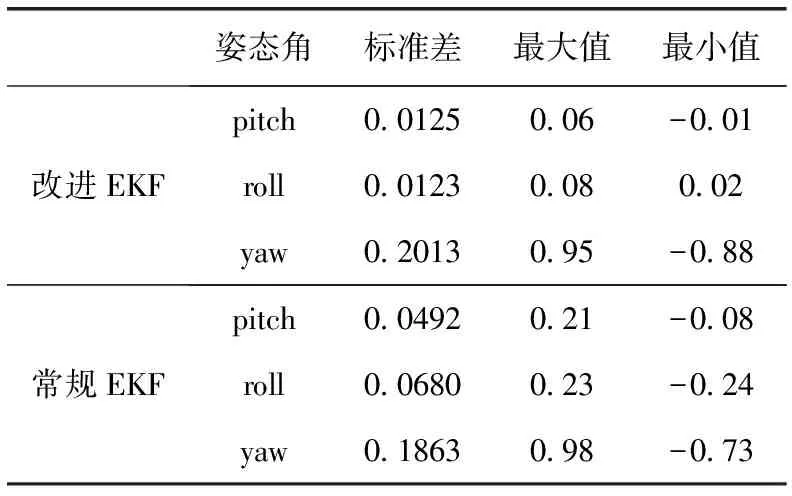
表2 静态实验两种算法的误差
3.2.3 水平滑动实验
水平滑动实验将四旋翼飞行器放置在水平的平台上,沿着任意的方向来回的水平滑动。两种算法水平滑动实验姿态角数据如图6所示, 根据图6姿态角的数据得到两种算法水平姿态角的标准差和波动范围见表3。当存在非重力运动加速度时,两种算法的水平姿态角都会受到一定的影响,但是改进EKF姿态估计算法波动范围比较小、而且更加稳定。从该组水平滑动实验对比可得,在非重力运动加速度下,改进EKF姿态估计算法的精度明显优于常规EKF姿态估计算法,而且有效抑制非重力运动加速度对姿态解算的影响。
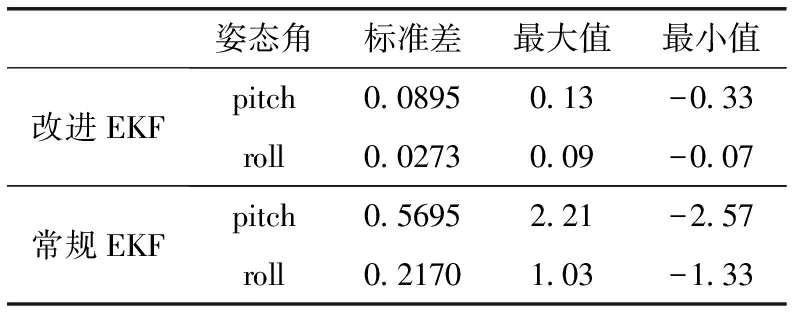
表3 水平滑动实验两种算法的误差
3.2.4 绕轴转动实验
绕轴转动实验将四旋翼飞行器分别绕着x轴和y轴从-70°到70°来回转动3次,分别采集两种姿态估计算法的pitch角和roll角。两种姿态估计算法的姿态角结果如图7所示。两种姿态估计算法的随动性都很好,都能够跟随着机体的快速转动实时精准的解算出姿态。图7中局部区域放大如图8所示,改进EKF姿态估计算法比常规的EKF姿态估计算法的曲线更加平滑。由该组对比实验可得,改进EKF姿态估计算法在快速转动过程中姿态更加平滑,动态性能优于常规EKF姿态估计算法。
4 结束语
本文提出一种基于共轭梯度的扩展卡尔曼姿态估计算法。该改进EKF姿态估计算法把基于共轭梯度算法估计出来的姿态四元数引入到观测模型,避免了观测模型线性化带来的误差,提高了估计精度。然后将非重力运动加速度引入到噪声协方差矩阵,实现噪声的自适应动态估计,抑制非重力运动加速度对姿态估计的影响,采用倾角补偿的方法单独计算偏航角,提高了四旋翼飞行器抗干扰能力。
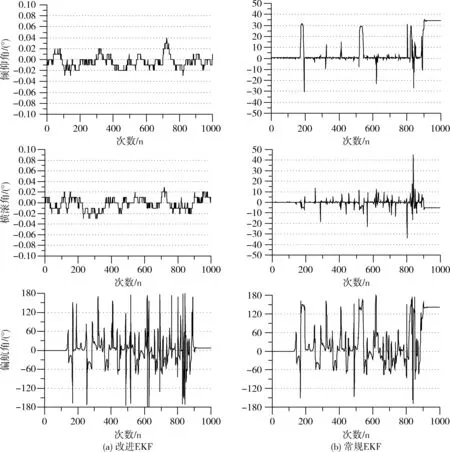
图5 抗磁干扰实验姿态角
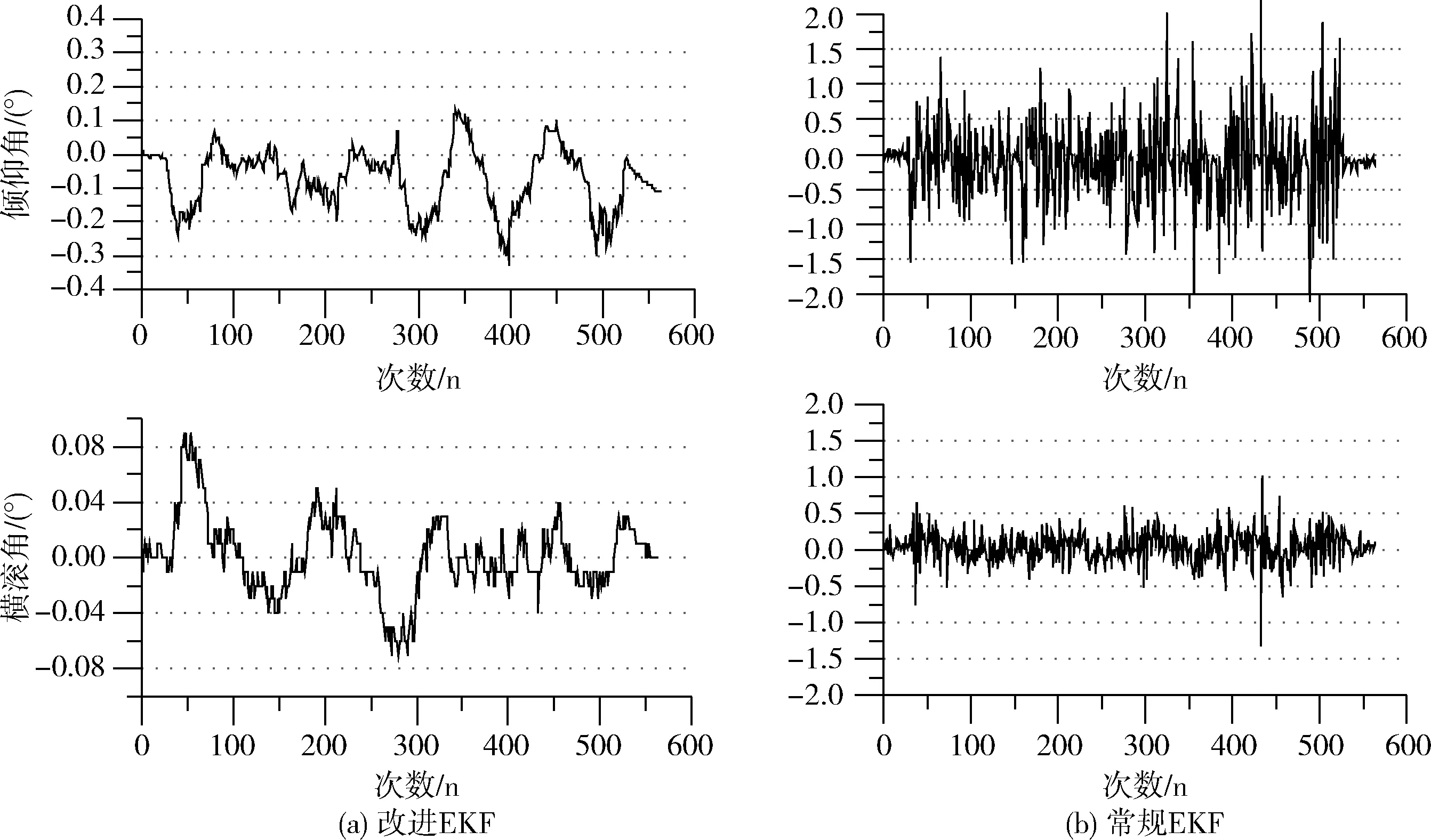
图6 水平滑动实验姿态角

图7 绕轴转动实验姿态角
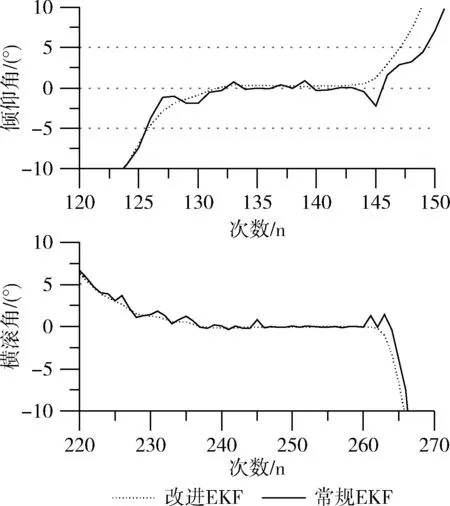
图8 图7局部区域放大图
实验结果表明:改进EKF姿态估计算法提高了姿态估计的精度,在机体快速运动的情况下,能够实时精准的解算出姿态角并且有效抑制非重力运动加速度对姿态估计造成的影响,在磁干扰下能够确保四旋翼飞行器的水平姿态不受影响,保证四旋翼飞行器的稳定飞行。
