基于DNA编码的多图像加密算法
2018-10-24孙鹤鹏张晓强
孙鹤鹏,张晓强
(中国矿业大学 信息与控制工程学院,江苏 徐州 221116)
0 引 言
多图像加密作为一种新兴多媒体安全技术,逐渐引起人们的关注。研究者们已提出一些基于光学信息处理系统的多图像加密算法[1-5]。如:朱等提出了一种基于小波变换的多图像加密算法[6];李等提出了一种基于级联分数阶傅里叶变换的多图像加密算法[7]。然而,这些算法中的大部分都是基于变换域而设计的,并常与图像压缩技术结合。因此,解密图像往往存在一些明显的失真。唐等提出了一种基于位平面和混沌映射的多图像加密算法[8]。然而,该算法每次只能加密四幅图像。
为保障多图像内容传输的安全性,结合混沌理论和DNA计算技术,提出了一种多图像加密算法。实验结果和算法分析表明:该算法加密效果良好,安全性高。
1 理论基础
1.1 DNA编码与运算
(1)DNA编码
DNA序列由腺嘌呤(A)、鸟嘌呤(G)、胞嘧啶(C)和胸腺嘧啶(T)组成。其中,A与T互补,G与C互补[9]。在二进制中,0和1互补,00和11、10和01也互补,用A、C、G、T编码00、01、10、11共有24种编码方案,但只有8种编码方案满足DNA碱基间的互补规则,请参见文献[10]。
通常,灰色图像的像素值可用8个比特来表示。然而,使用DNA编码规则,灰色图像的像素值也可用4个DNA码来表示。反之,根据给定DNA序列可得出相应的十进制像素值。
(2)DNA运算
DNA序列的加、减法运算是根据二进制系统中的加、减法运算得到的。根据DNA编码规则1,DNA序列的加、减法运算,请参见文献[10]。
1.2 二维Logistic混沌映射
二维Logistic混沌映射定义为

(1)
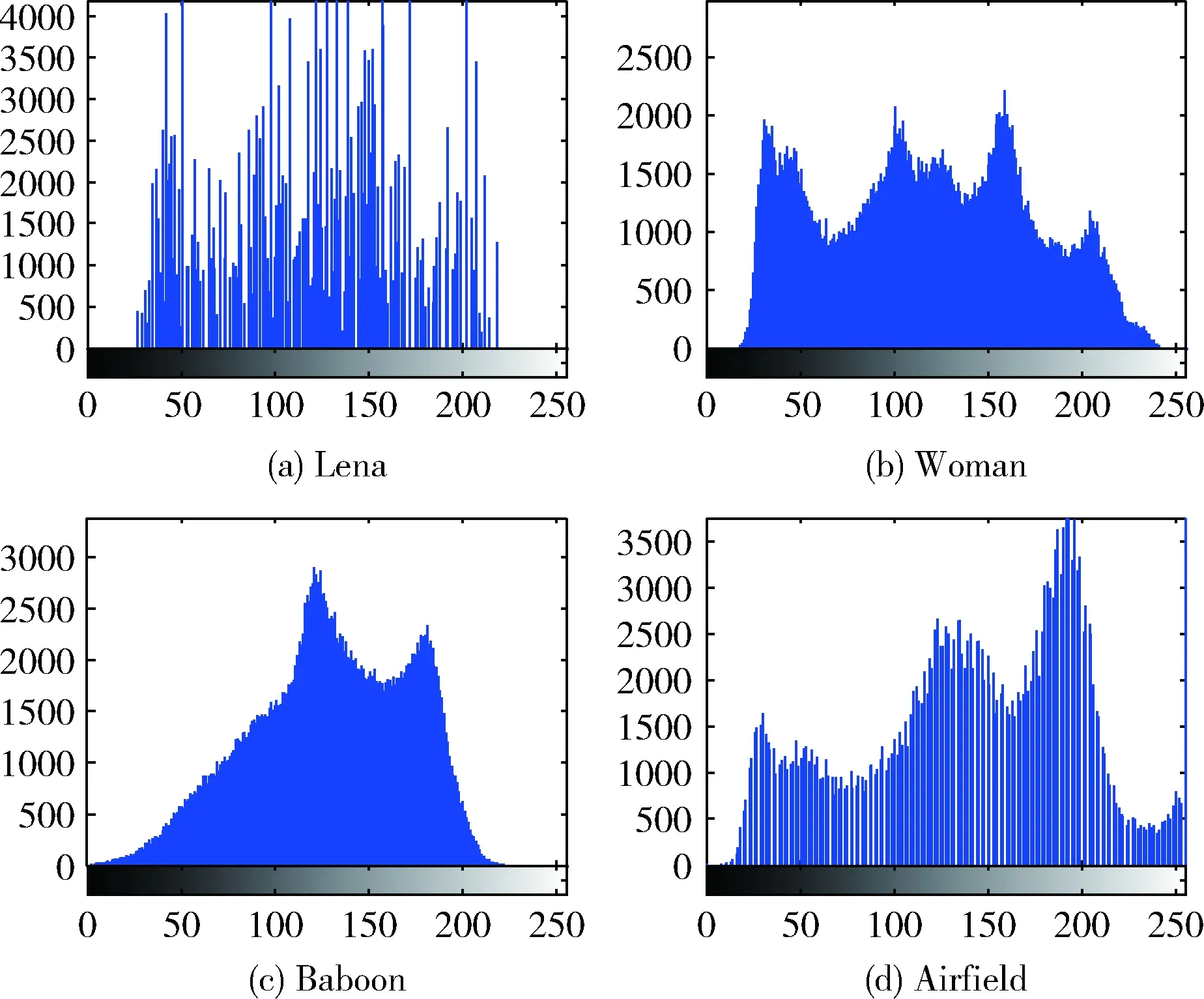
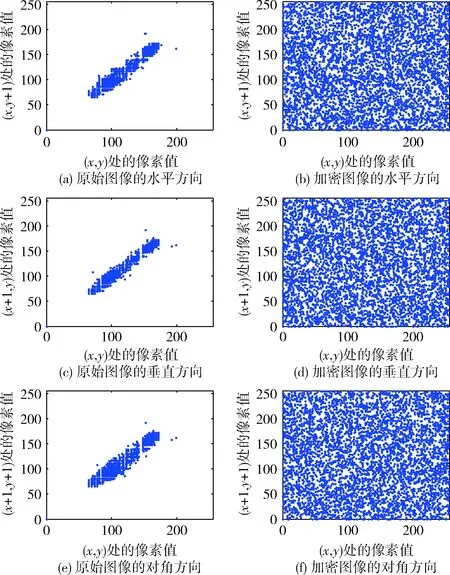
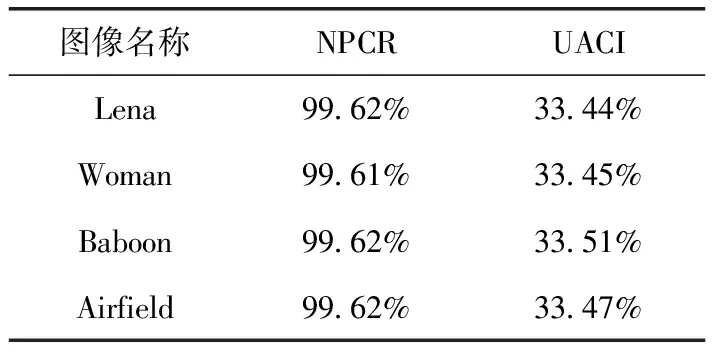
式中:r1,r2,s1和s2是用于控制二维Logistic混沌行为的系统参数。当2.75 安全散列算法(secure hash algorithm)既可用于数字签名标准算法,也可为数据的完整性验证服务[11]。SHA-256是一种安全散列算法,摘要长度为256比特。为增强明文敏感性,新算法利用SHA-256产生混沌系统的初始值,即使两幅原始图像只有一个比特的差别,它们的哈希值也会完全不同[11]。 将k幅原始图像组合为一幅大图像,根据组合图像,利用SHA-256产生256比特哈希值K。以8比特为一个比特块ki,则K可表示为 K=k1,k2,…,k32 (2) 二维Logistic映射的初始值可表示为 (3) (4) 新算法的加密流程,如图1所示。首先,分别对k(k> 2)幅原始图像进行DNA编码;其次,利用二维Logistic映射产生的混沌序列,将DNA序列在k幅图像间移动进行置乱;再次,将置乱图像与二维Logistic映射产生的混沌图像进行加法运算完成扩散过程;最后,进行DNA解码,得到加密图像。其中,二维Logistic映射初始值由2.1节方法产生。具体加密步骤为: 图1 加密流程 步骤1 将k幅大小为m×n的原始图像I1,I2,…,Ik组合为一幅大图像。利用2.1节方法产生二维Logistic映射的初始值x0和y0。 步骤2 利用x0和y0,迭代二维Logistic映射4mn次,产生2个混沌序列X4mn和Y4mn。 步骤3 对I1,I2,…,Ik分别进行DNA编码,得矩阵I11,I21,…,Ik1。 步骤4 计算 (5) 步骤5 置乱k幅DNA编码图像 (6) 式中:i=1,2,…,m和j=1,2,…,4n。 最后,可得置乱矩阵I12,I22,…,Ik2。 步骤6 按照一定规则,从Y4mn选取m×n个元素构成Zmn。计算 (7) 步骤7 对I12,I22,…,Ik2按照下式进行扩散得矩阵I13,I23,…,Ik3 It3(i,j)=It2(i,j)+C(i,j) (8) 式中:t=1,2,…,k,i=1,2,…,m和j=1,2,…,4n。 步骤8 对I13,I23,…,Ik3分别进行DNA解码,得加密图像E1,E2,…,Ek。 解密步骤为加密步骤的逆过程。 图2 原始图像 图3 加密图像 直方图显示了一幅图像中像素值的分布情况,好的加密算法的加密图像应该有均匀的直方图。图4和图5分别为原始图像和加密图像的直方图。从图可看出:原始图像的直方图和对应加密图像的直方图完全不同,加密图像的直方图类似噪声分布,从而掩盖了原始图像的统计特征。因此,攻击者不能从加密图像中发现有用的统计数据,这表明新算法可有效地抵抗统计攻击。 图4 原始图像的直方图 图5 加密图像的直方图 根据如式(9),可计算原始图像和加密图像中相邻像素的相关性rx,y (9) (10) (11) 其中,E(x)和D(x)分别为x的期望和方差。 选取图像中多对相邻像素,进行相关性分析。图6为原始图像Lena及其加密图像的相关性分析。原始图像和加密图像的相关系数,见表1。实验结果显示:在原始图像中,相邻像素的相关系数均接近1,与此相对,在加密图像中,相邻像素的相关系数均趋近0。因此,新算法能够破坏原始图像相邻像素的相关性,从而很好地保护原始图像内容的安全。 图6 原始图像和加密图像的相关性分析 表1 原始图像和加密图像的相关系数 图7 错误解密图像 像素数目改变率和平均强度变化率是图像加密学者进行差分攻击分析的两个常见指标。两个指标值越大,表明该加密算法对明文变化越敏感,算法抵制差分攻击的能力越强。它们定义分别如式(13)和示(14)所示 (12) (13) (14) 其中,I′(i,j)和I″(i,j)分别为原始图像修改前后对应的加密图像。 在实验中,随机选取原始图像Lena中的任选一个像素,如I(1,1)=158。为测试新算法抵制差分攻击的能力,将该像素的像素值改为200。加密图像的像素数目改变率和平均强度变化率,见表2。从表中数据可看出:即使对原始图像做出轻微的改动,也会对加密图像造成巨大的影响。同时,也说明新算法具有良好的抵制差分攻击的能力。 表2 加密图像的NPCR和UACI 信息熵能够反映一幅灰色图像像素灰度值的分布状况。如果像素灰度值分布较为水平一致,那么该图像的信息熵就会较大。一幅理想的随机图像,所有灰度级出现的概率完全相等。此时,可计算出信息熵为8。因此,当加密图像的信息熵越接近8时,说明图像像素值改变的越充分,加密效果越好[13]。信息熵定义为 (15) 表3 加密图像的信息熵 在唐算法[8]中,4幅加密图像被视为PNG图像的红、绿、蓝和阿尔法分量。因此,该算法每次只能加密4幅原始图像。然而,新算法每次能加密多幅原始图像,具体数目根据用户需求来确定。因此,新算法在加密图像数目上优于唐算法[8]。 张算法[14]仅置乱了图像块位置,没有进行扩散操作。因此,张算法适用于加密效率要求高,而安全性要求相对不太高的应用场景中[14]。然而,新算法进行了置乱和扩散操作。同时,随着加密图像数目的增加,新算法的置乱过程效果会更好,安全性更高。因此,新算法在安全性上优于张算法[14]。 结合DNA和二维Logistic映射,提出了一种多图像加密算法。该算法每次可加密多幅图像。与两种类似算法对比表明:新算法具有一定的优势。实验结果和算法分析表明:新算法足以抵抗蛮力、差分、统计和选择明文等攻击,安全性高。未来,随着DNA技术的发展,新算法在加密效率上的优势将得到充分体现。1.3 安全散列算法
2 加密算法
2.1 混沌映射初始值的产生

2.2 加密步骤

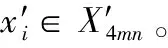

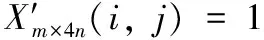

2.3 解密步骤
3 仿真实验



4 算法分析
4.1 密钥空间分析

4.2 直方图分析

4.3 相关性分析

4.4 密钥敏感性分析


4.5 差分攻击分析
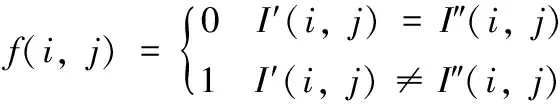
4.6 信息熵分析


5 与类似算法对比分析
5.1 输入图像数目分析
5.2 安全性分析
6 结束语
