你绕路了吗？

季黎明

伴随着“轴对称图形”这一章节学习的结束，我们遇到了越来越多的路径最值问题，下面就其中常见的两种错误题型进行剖析.

【例1】如图1，A、B是两个蓄水池，都在河岸l的同侧.为了灌溉作物要在河岸建一个抽水站P，将河水送到A、B两地.问该站P建在河岸什么地方，可使所修的渠道最短，试在图中确定该点P.

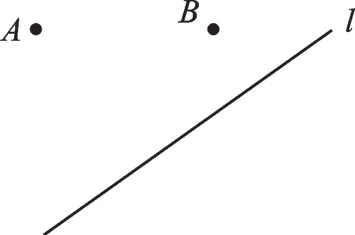
图1

图2

【错解】如图2，过点A作AP⊥l，垂足即为点P.

【纠错】我们将该问题转为数学问题，即在l上寻找一点P使得PA+PB取得最小值.上述解答中AP⊥l仅满足了PA最短，而这并不能保证PA+PB的值最小，所以，解决该问题我们需要将视线从局部最值转移到整体最值来考虑.

【正解】作点A关于l的对称点A1，在l上任取点P（如图3），由对称性得：PA=PA1，则PA+PB=PA1+PB.根据两点之间线段最短，当P、A1、B三点共线时，PA1+PB最短且等于A1B.所以连接A1B交直线l于点P，点P即为所求（如图4）.

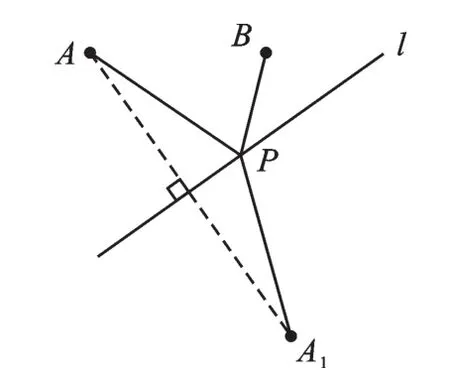
图3

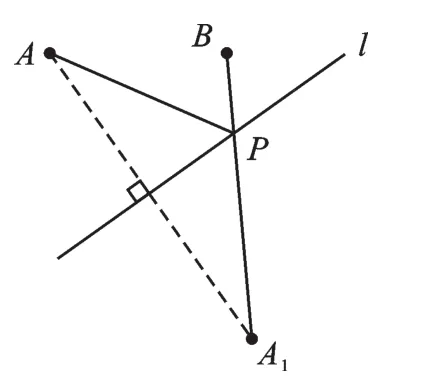
图4

【例2】如图5，两条公路OA、OB相交，在两条公路的中间有一个油库，设为点P.如果在两条公路OA、OB上各设置一个加油站C、D，请你设计一个方案，把两个加油站设在何处，可使运油车从油库出发，经过一个加油站，再到另一个加油站，最后回到油库所走的路程最短.

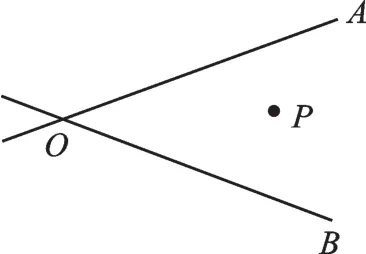
图5

图6

【错解】如图6，过点P作PC⊥OA于C，PD⊥OB于D，垂足分别为点C、D.

【纠错】同样地将该问题转为数学问题，即要求在射线OA、OB上寻找合适的点C、D，使得PC+CD+PD三条线段之和作为整体取得最小值.在上述解答中PC⊥OA、PD⊥OB仅满足PC和PD最小，忽略了线段CD的长度对整体最值的影响.

图7

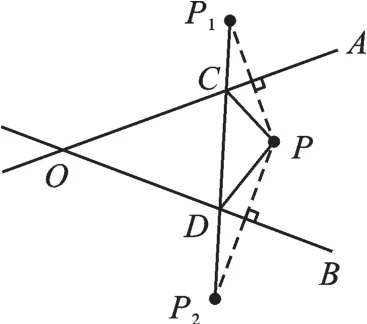
图8

【正解】分别作点P关于OA、OB的对称点P1、P2，在射线OA、OB上任取点C、D（如图7），由对称性可知：CP=CP1，DP=DP2.则 PC+CD+PD=CP1+CD+DP2.根据两点之间线段最短，当P1、C、D、P2四点共线时，CP1+CD+DP2最短且等于P1P2.所以，连接P1P2交OA、OB于点C、D，点C、D即为所求（如图8）.

【总结】路径最短问题通常涉及多条线段的和，我们需要认识到个别线段取得最小值并不能确保整体也取得最小值.针对此类问题，我们可以利用轴对称性质，将线段和转化为两点之间的线段长，这是解决问题的常用策略.