善用基本模型，速求最小值

钱玉玲

求两条或两条以上线段和的最小值问题，是同学们的“老朋友”了.解决这类问题的策略很多，其中利用轴对称变换转化线段，是一种重要的方法.分析这类问题时，我们一般要先分析相关点是定点还是动点，往往动点个数越多，难度越大.下面就两个定点两个动点（简称“两定两动”）型线段和的最小值问题与同学们一起探讨，期待给同学们一些启发.

【基本模型】如图1，点A、B是锐角MON外部任意两个定点，在∠MON的两边OM、ON上分别确定点P、Q，使得AP+PQ+QB的值最小.

图1

图2

【解析】A、B两点确定，P、Q两点分别是OM、ON上的动点，如图2，根据“两点之间线段最短”，连接AB与OM、ON分别交于点P、Q，点P、Q即为所作.接下来运用这一基本模型解决问题.

【例1】如图3，点A、B分别是锐角MON内部、外部一点，在∠MON的两边OM、ON上各找一点P、Q，使得AP+PQ+QB的值最小.

图3

图4

图5

【解析】显然，连接AB无法解决问题.类比基本模型，相同之处是A、B两点是定点，P、Q两点是动点；不同的是定点A在∠MON的内部.那么能否转化为基本模型呢？如图4，作点A关于OM的对称点A′，由轴对称性质可知PA′＝PA，则AP＋PQ＋QB＝A′P＋PQ＋QB，所以当A′P+PQ+QB的值取最小时，AP+PQ+QB的值最小.观察图4，点A′、B在∠MON的外部，与基本模型一致，连接A′、B即可（如图5）.

【变式】如图6，点A、B是锐角MON内部任意两点，在∠MON的两边OM、ON上各找一点P、Q，使得AP+PQ+QB的值最小.

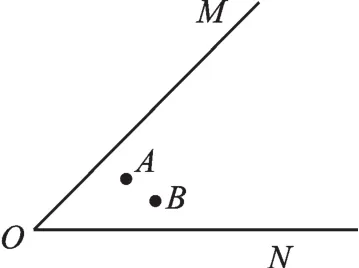
图6

图7

图8

【解析】类比例1，只需为A、B两个定点寻找“替身”，转化到∠MON的外部即可.显然，轴对称及轴对称的性质是寻找“替身”的“出路”（如图7），结合基本模型，连接A′B′，即可解决问题（如图8）.

【实际应用】某中学八（2）班举行元旦晚会，桌子摆成如图9所示的两直排（图中OA、OB）.OA桌面上摆满橘子，OB桌面上摆满糖果.站在C处的小明同学先拿橘子，再拿糖果，然后到D处的座位上.请你帮他设计一条行走路线，使其所走路程最短.

图9

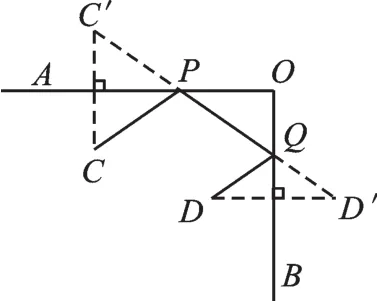
图10

【解析】先将实际问题转化成数学问题.两排桌子构成了∠AOB，小明出发地C和座位D可看成∠AOB内部两个定点，根据前面的解题经验，只需分别作出点C关于OA的对称点C′，点D关于OB的对称点D′，连接C′D′与OA、OB分别交于点P、Q，点P、点Q即是小明拿橘子、糖果的位置（如图10）.

同学们，“题海”茫茫，在学习的过程中，要善于总结归纳基本图形；在其他具体问题情境中，学会利用“转化”思想向基本模型“靠拢”，可以达到事半功倍的效果.