塑壳断路器触头终压力的公差仿真分析

袁亦峰



塑壳断路器触头终压力的公差仿真分析

袁亦峰

（德力西电气有限公司上海分公司，上海 201812）

本文以塑壳断路器触头终压力为优化目标，以计算机辅助公差分析为基础，引入受力分析、尺寸敏感度分析和权重分析，优化影响触头终压力的相关尺寸公差及弹簧刚度系数。分析结果表明，相比以往的只有理论名义值的力值，在考虑力的公差分析以后，对于力的计算不仅有理论值，而且还有公差范围，并根据现有的工艺水平，提出了合理优化触头终压力的改进方案。

塑壳断路器；公差仿真分析；触头终压力

随着计算机技术的进步和人们对产品质量要求的提高，计算机辅助发展领域从CAD（计算机辅助设计）、CAM（计算机辅助制造）、CAE（计算机辅助工程），延伸到CAT（计算机辅助公差）领域。为了提高产品的客户满意度，同时为了达到节能降本等需求，一种关注产品功能的设计方法也在制造业领域进行推广，这就是功能设计方法[1]。功能设计方法需要的一项核心技术便是尺寸链计算及其公差设计。在零部件加工的时候，会因为设计基准、加工基准与测量基准不一致以及设备的加工精度等因素的制约，在零件加工环节，必须考虑预留加工余量，需要进行工艺尺寸链的设计；此外，在装配环节，由于零件本身的加工精度以及装配时的定位误差，会造成一系列的误差积累，这将对机器的工作性能造成不同程度的影响，严重时机器将丧失应有的功能。基于上述公差积累问题，文献[2]提出了功能设计方法。其基本思想是：建立零件的功能尺 寸误差和产品功能条件误差之间对应的影响关系。一般的设计师缺乏有效的公差分析工具，对公差的分配往往依据经验或通过增加样机数量，采用试凑法，在“试验—改进—试验”的繁复工作中耗费大量时间。但面对产品更新换代的加快，这种方法往往难以奏效，且缺乏理论依据，这种弊端困扰着设计师，因此制造业尤其是其中的高端行业迫切需要新的方法、新的工具来进行尺寸链设计。

尺寸链设计从维度上讲，经历了从一维线性尺寸链到二维、三维非线性尺寸链的过程；从公差分布上讲，经历了从算术公差到统计公差的过程，在这些发展过程中，陆续产生了许多新的公差理论，比如矢量公差设计、鲁棒公差设计、并行公差设计和关于形位公差设计等新理论。在这些理论满足尺寸链求解方程日益复杂（多维度、多变量、多目标函数）的同时，导致了计算非常繁琐，需要反复迭代，靠手动计算和简单编程已经无法满足分析和优化，需要开发专业的公差仿真分析软件来实现计算要求。目前的主流商用公差分析软件有CETOL、Tolerance Manager、3DCS等。

这些软件各有优点和特色，下面以Tolerance Manager（以下简称TM）为例，其借助Creo或Solidworks平台的草绘模型，依靠数形结合，不仅可以进行单纯尺寸的公差计算，而且可以进行静力学分析，进行力值的公差计算，而且对一些不能直接测量的物理量，可以通过函数构造进行分析。不仅能轻松求解线性尺寸链，而且还能方便、稳妥地求解复杂的非线性尺寸链，在公差分布方面还能综合概率统计，针对产品存在多个静态位置[3]，可以构造多个尺寸链草绘模型，将这些尺寸链方程进行联合求解。

低压电器及中高压电器行业，是国内较早地应用尺寸链及公差仿真软件来辅助产品设计的行业之一，其中文献[4-9]均介绍了应用实例。在塑壳断路器的参数中，触头终压力是一个较为关键的控制项，它的大小关系到断路器的分断能力、温升、寿命等。触头终压力既不能偏小，也不能过大，必须控制在合理的范围内；其中，找出那些对触头终压力的敏感度比较高的功能尺寸[2]以及如何控制它们，是设计师较为关心的。本文以某规格塑壳断路器合闸状态时的触头终压力作为研究对象，在Creo平台上进行草绘建模，利用TM的静力学模块计算触头终压力的名义值，然后进入TM公差仿真模块，对相关尺寸和参数进行了优化，得到了触头终压力的尺寸链计算的结果。将计算结果和实际测量值对比，根据现有的工艺水平，找出那些敏感度较高的参数，提出控制方案，以确保触头终压力的公差控制在合理的范围内。

1 尺寸链及公差计算理论

1.1 尺寸链要素

1）尺寸链的函数表达

以触头终压力分析为例，将触头终压力定义为，也称功能条件，它在尺寸链中是封闭环，而尺寸链中其他的尺寸以及参数则为组成环，也称功能尺寸，不妨将这些功能尺寸定义为1,2,3,…,x。把记作(1,2,3,…,x)，它的数学意义是：(1,2,3,…,x)是1,2,3,…,x的多元函数，1,2,3,…,x是函数的自变量。

2）敏感度

敏感度是描述尺寸链中各个功能尺寸的变化对功能条件的影响程度，其变化大小和变化方向用数学公式表达，有

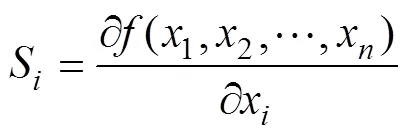
式中，S为某一个功能尺寸的敏感度；1,2,3,…,为尺寸连上的组成环；x为某一个功能尺寸。

敏感度的数学意义为功能条件对某个功能尺寸x的一阶偏导数。敏感度的工程意义是：若S符号为正，则在这个尺寸链中，功能尺寸x是增环；反之，则为减环。S的绝对值越大，此时x对的影响就越大。敏感度的数值为设计师进行优化设计指明了方向。设计师可以根据敏感度，调整功能尺寸的名义值，达到优化设计的目的。

3）影响因子

影响因子的工程意义是功能尺寸x的公差带TR对给定的功能条件的实际影响，定义为E，其数学表达式为

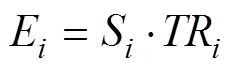
4）权重

权重的意义是，在某一个功能条件的所有影响因子中，其中第个功能尺寸x所对应的E的平方，占所有影响因子的平方和的比重。将其定义为W，其数学表达式为

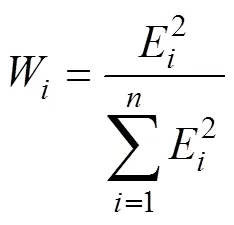
1.2 公差计算理论

1）极值法

极值法是建立在完全互换的基础上，其思路是，功能条件下的所有功能尺寸x（=1, 2,…,），根据S的符号进行分组，将S（=1, 2,…,）＞0编为一组，将S（=1, 2,…,）＜0编为一组，显然+=。此时

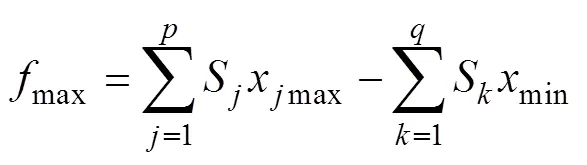
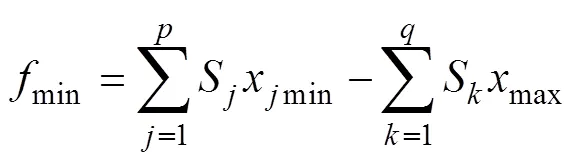
则的公差带大小为

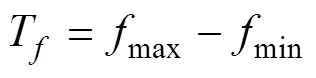
2）概率统计法

这种方法通常假设功能条件（封闭环）的概率分布接近于正态分布，偏差在6内，那功能条件的统计公差为

式中，S为组成环（功能尺寸）的敏感度；0、K为封闭环和第个组成环（功能尺寸）的相对分布系数；TR为第个组成环（功能尺寸）的公差。

3）随机模拟方法

也称蒙特·卡洛（Monte Carlo）方法。它的基本思想是，为了求解数学、物理、工程技术以及生产管理等方面的问题。首先建立一个概率模型或随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征；最后给出所求解的近似值，解的精度可用估计值的方差来表示。

2 尺寸链模型构建

本文以塑壳断路器为例，塑壳断路器触头合闸状态时静触头对动触头的反作用力（触头终压力）作为研究对象，利用尺寸链公差仿真软件Creo/TM对触头终压力进行分析。塑壳断路器由壳体、操作机构、触头系统、热磁系统、灭弧系统、接线端子、绝缘件等组成，其模型如图1所示。

1—壳体；2—静触头；3—动触头；4—操作机构；5—热磁系统

触头终压力是塑壳短路器的重要参数之一，对产品的分断能力、温升、寿命等有直接影响。塑壳断路器触头终压力简图如图2所示，为触头反力，根据牛顿第三定律，触头终压力与触头反力大小相等，方向相反。产品合闸后，塑壳断路器的状态草绘模型图如图3所示。

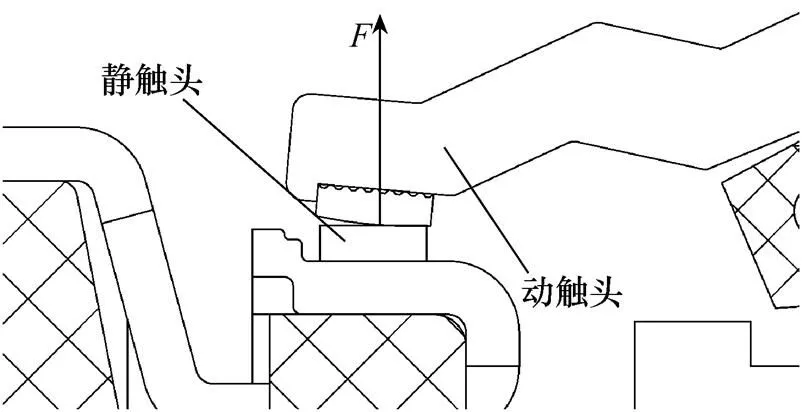
图2 塑壳断路器触头终压力简图

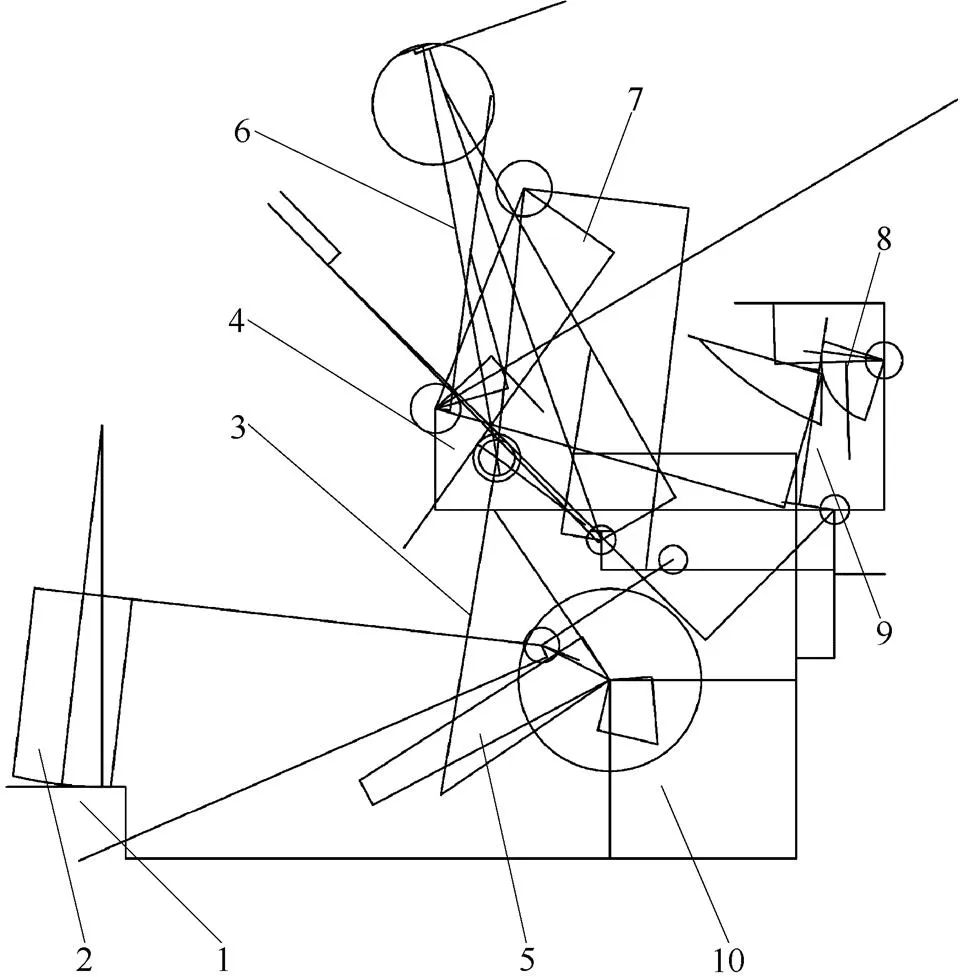
1—静触头；2—动触头；3—下连杆；4—支架；5—转轴； 6—杠杆；7—跳扣；8—再扣；9—锁扣；10—壳体

3 公差仿真与优化

3.1 静力学模型构建

在Creo中完成草绘以后，进入TM的静力学模块进行静力学前处理及分析，依次定义零件、运动副、摩擦因素，添加激励，定义功能条件，最后进行解算，过程如图4所示。

定义机构的机架，如图5所示，选择基座，并定义组，同一个组当中的零件绑定在一起，没有相互运动关系。

定义零件后，按图6所示在零件连接部位进行运动副定义，运动副类型、摩擦的定义如图7所示。

在低压电器领域，常用的内部激励为弹簧。本文中，共有3处弹簧，即机构主拉簧、触头弹簧和锁扣弹簧。以触头簧为例，为了简化模型，将三相触头上的扭簧合成并等效到中间相，按如图8（a）所示的位置添加扭簧激励，按图8（b）所示设置扭簧参数。

图4 静力学计算模块菜单

图5 定义固定零件及固定组

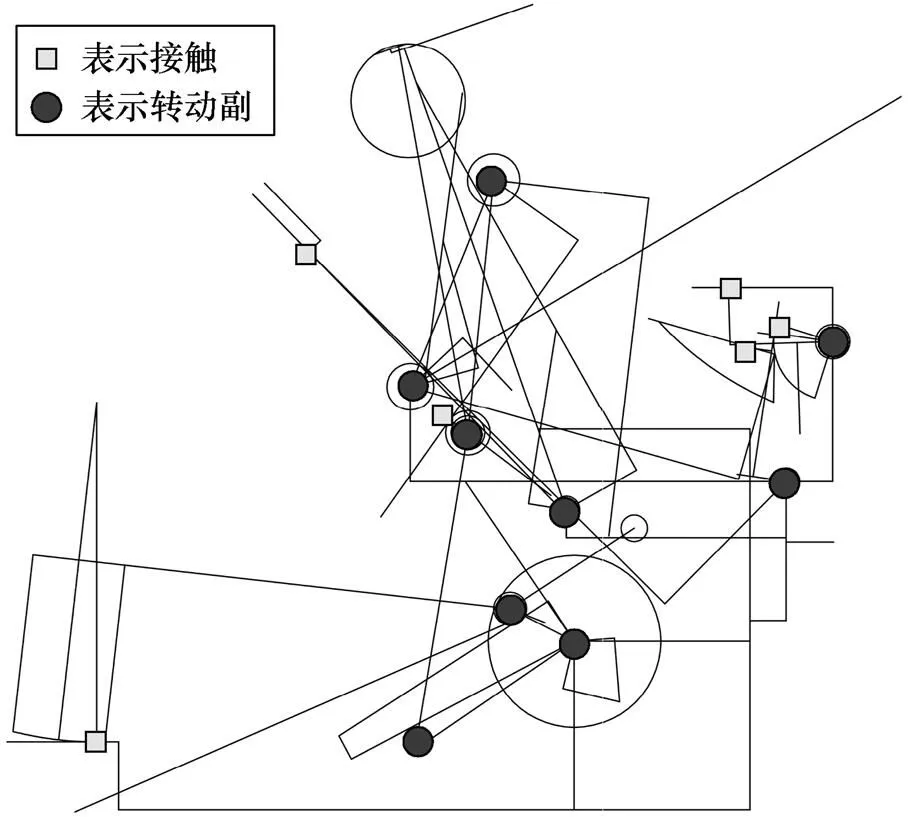
图6 静力学中的运动副图

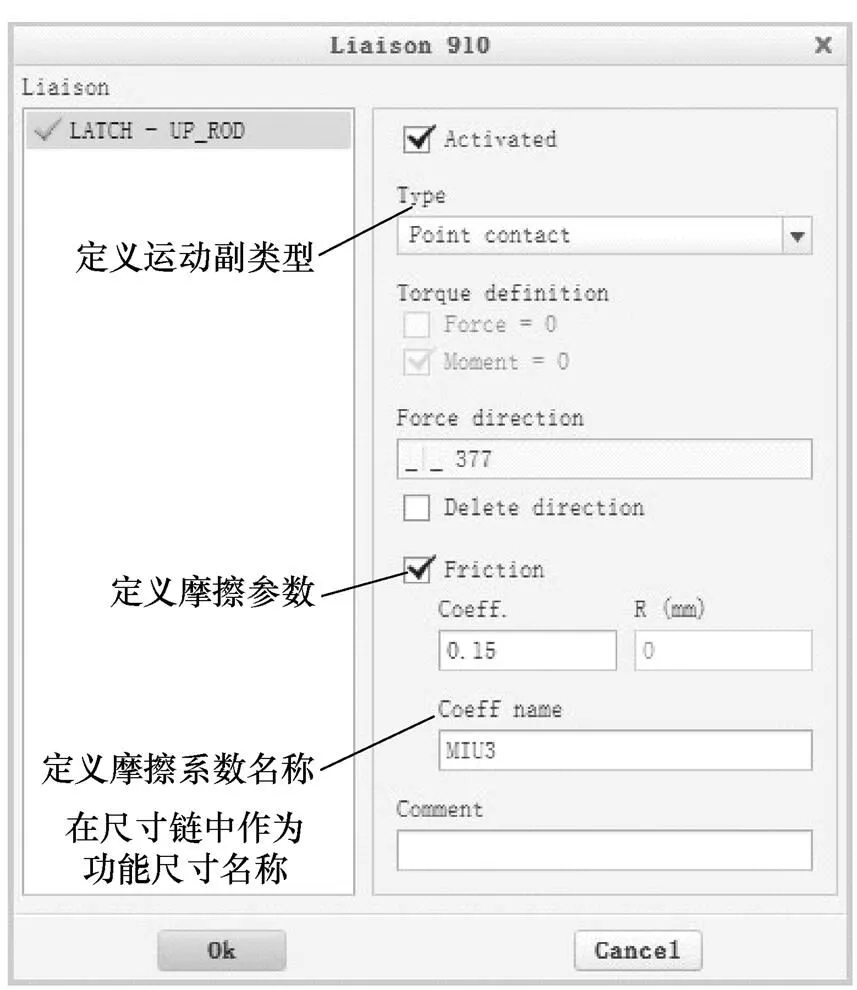
图7 运动副中的摩擦定义

图8 扭簧位置及参数设定

在选择摩擦力效果的时候，要根据实际情况，选择摩擦效果，在本文中如图9所示，选“Decrease”。

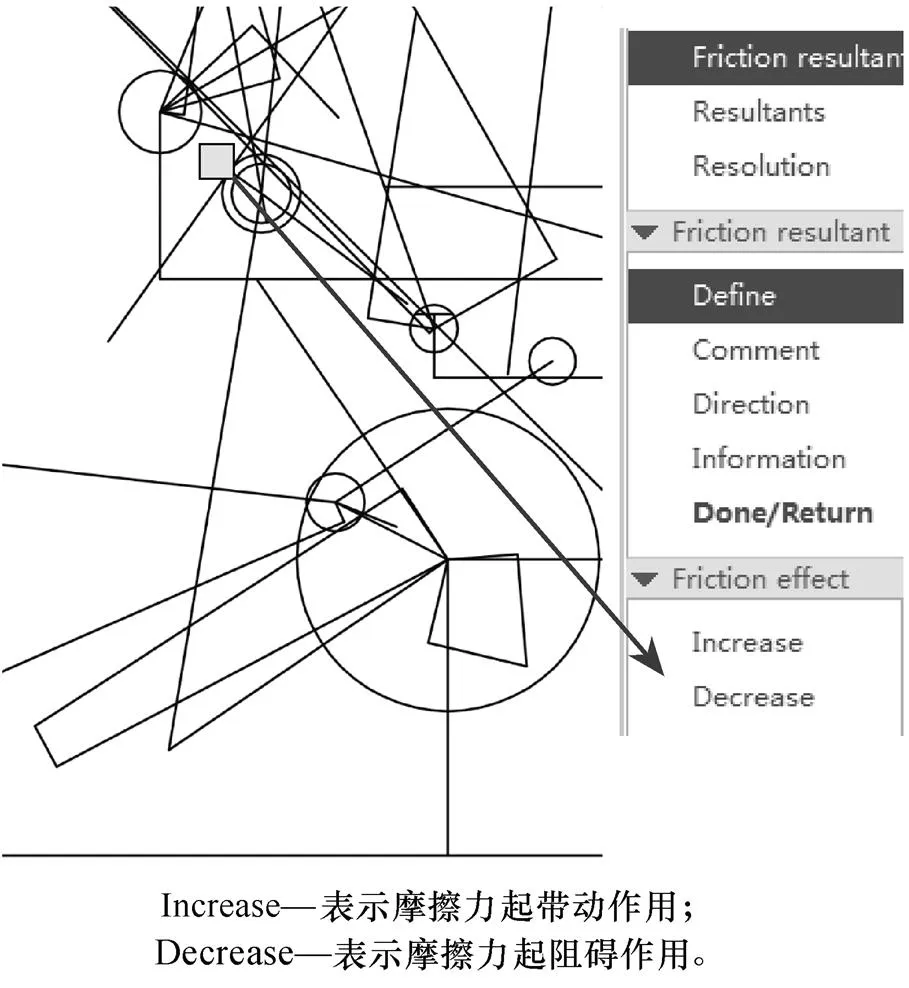
图9 定义摩擦力效果

定义终压力的功能条件，如图10所示。注意：箭头所指的方向并不是终压力的真正方向，而这只是一个受力符号。

图10 定义终压力的功能条件

完成上述定义以后，进行求解，如果之前的定义无误，则弹出报告文件，图11是报告文件的一个片段，图中定义的是三相触头反力总和及力相对于水平正方向的夹角。点击保存则生成以.i3e为尾缀的堆栈文件，这个个文件就可以导入3.2节中的TM主程序进行公差仿真分析，至此，前处理完毕。

图11 报告文件片段

3.2 尺寸链仿真计算

据统计，零件在制造过程中，公差分布并不服从标准正态分布，而是带中心偏移的正态分布；此外，在定义统计公差时还可以根据制程能力，通过CPK值进行定义，如图12所示。

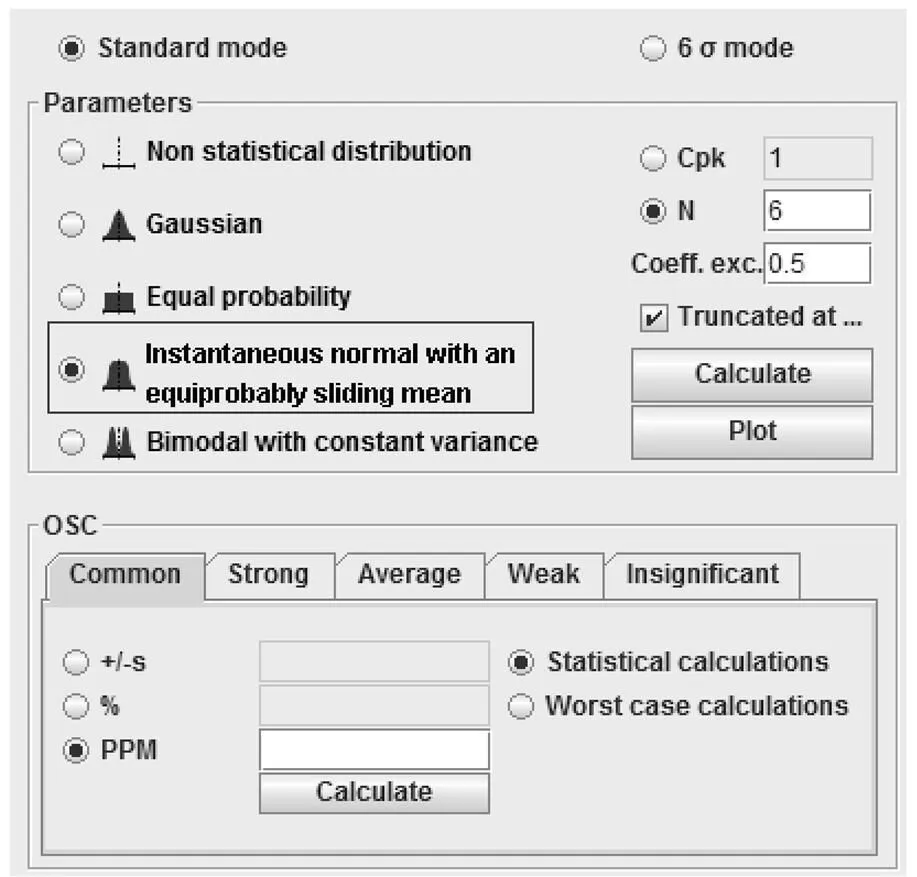
图12 统计公差的设置

表1的公差及名义尺寸是按照初始值输入的，可以看到与触头终压力有关联的零件及参数是外壳，上、下连杆，杠杆，触头弹簧的位置及刚度，转轴，动触头，机构支架，合闸限位轴的摩擦因素等。

表1 触头终压力有关的功能尺寸公差与敏感度、权重（调整前）

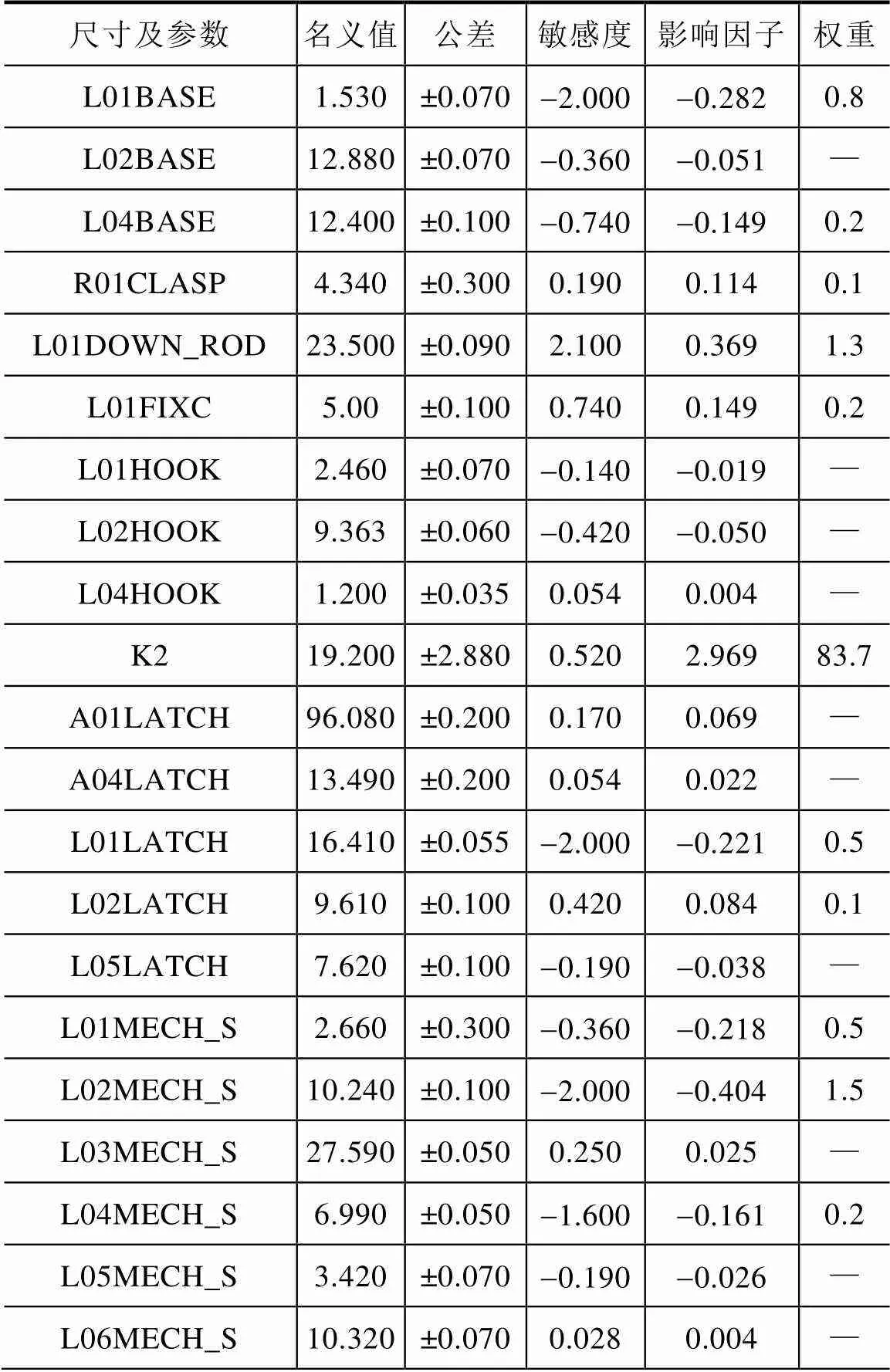
尺寸及参数名义值公差敏感度影响因子权重 L01BASE1.530±0.070-2.000-0.2820.8 L02BASE12.880±0.070-0.360-0.051— L04BASE12.400±0.100-0.740-0.1490.2 R01CLASP4.340±0.3000.1900.1140.1 L01DOWN_ROD23.500±0.0902.1000.3691.3 L01FIXC5.00±0.1000.7400.1490.2 L01HOOK2.460±0.070-0.140-0.019— L02HOOK9.363±0.060-0.420-0.050— L04HOOK1.200±0.0350.0540.004— K219.200±2.8800.5202.96983.7 A01LATCH96.080±0.2000.1700.069— A04LATCH13.490±0.2000.0540.022— L01LATCH16.410±0.055-2.000-0.2210.5 L02LATCH9.610±0.1000.4200.0840.1 L05LATCH7.620±0.100-0.190-0.038— L01MECH_S2.660±0.300-0.360-0.2180.5 L02MECH_S10.240±0.100-2.000-0.4041.5 L03MECH_S27.590±0.0500.2500.025— L04MECH_S6.990±0.050-1.600-0.1610.2 L05MECH_S3.420±0.070-0.190-0.026— L06MECH_S10.320±0.0700.0280.004—

（续）

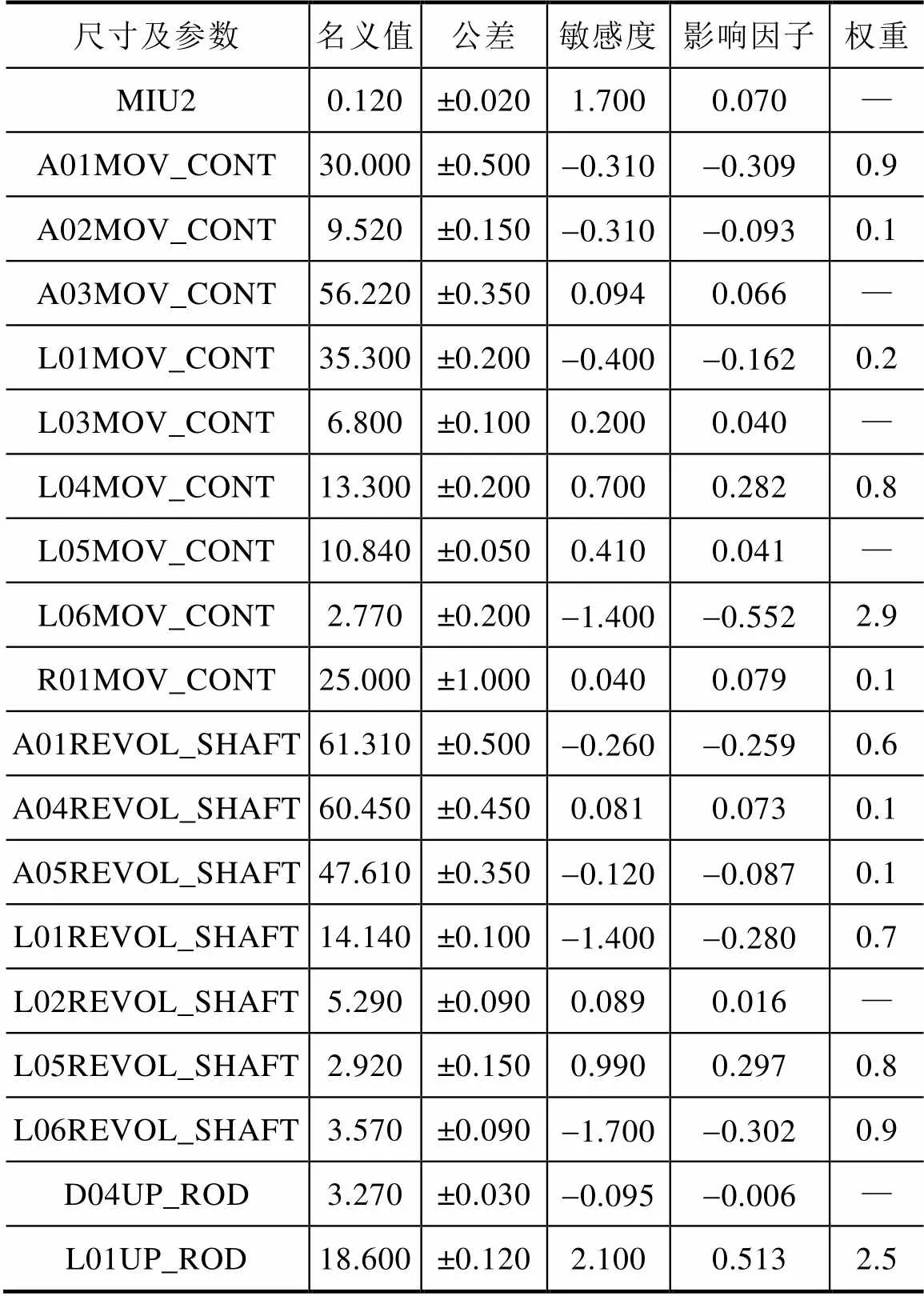
尺寸及参数名义值公差敏感度影响因子权重 MIU20.120±0.0201.7000.070— A01MOV_CONT30.000±0.500-0.310-0.3090.9 A02MOV_CONT9.520±0.150-0.310-0.0930.1 A03MOV_CONT56.220±0.3500.0940.066— L01MOV_CONT35.300±0.200-0.400-0.1620.2 L03MOV_CONT6.800±0.1000.2000.040— L04MOV_CONT13.300±0.2000.7000.2820.8 L05MOV_CONT10.840±0.0500.4100.041— L06MOV_CONT2.770±0.200-1.400-0.5522.9 R01MOV_CONT25.000±1.0000.0400.0790.1 A01REVOL_SHAFT61.310±0.500-0.260-0.2590.6 A04REVOL_SHAFT60.450±0.4500.0810.0730.1 A05REVOL_SHAFT47.610±0.350-0.120-0.0870.1 L01REVOL_SHAFT14.140±0.100-1.400-0.2800.7 L02REVOL_SHAFT5.290±0.0900.0890.016— L05REVOL_SHAFT2.920±0.1500.9900.2970.8 L06REVOL_SHAFT3.570±0.090-1.700-0.3020.9 D04UP_ROD3.270±0.030-0.095-0.006— L01UP_ROD18.600±0.1202.1000.5132.5

需要说明的是，考虑到改产品为3极产品，表1中触头弹簧刚度2值为单根弹簧刚度的3倍，同时功能条件是经过函数构造的，是单个触头的平均终压力，即为原来静触头总反力的1/3，如图13所示。

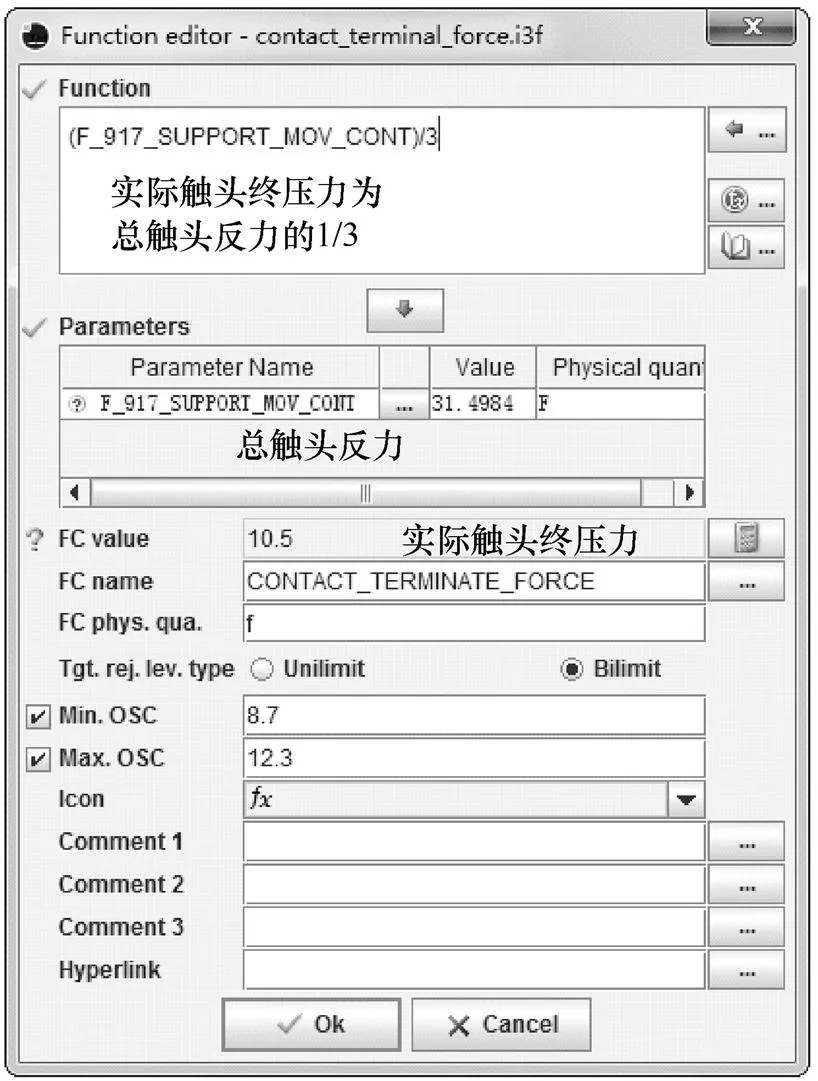
图13 功能条件的函数构造

功能条件（封闭环）的名义值、公差范围、概率分布以及每百万分之不良率如图14所示，可知，触头的合格的设置范围是8.7～12.3N；统计法计算得到8.159～11.74N；极限法得到5.25～14.38N；均未满足设计要求；根据统计计算，不良率达到5678/PPM，不符合设计要求（设计要求是不良率小于50/PPM），且触头终压力的值对比设计值是偏小的，需要对相关功能尺寸、公差进行调整。

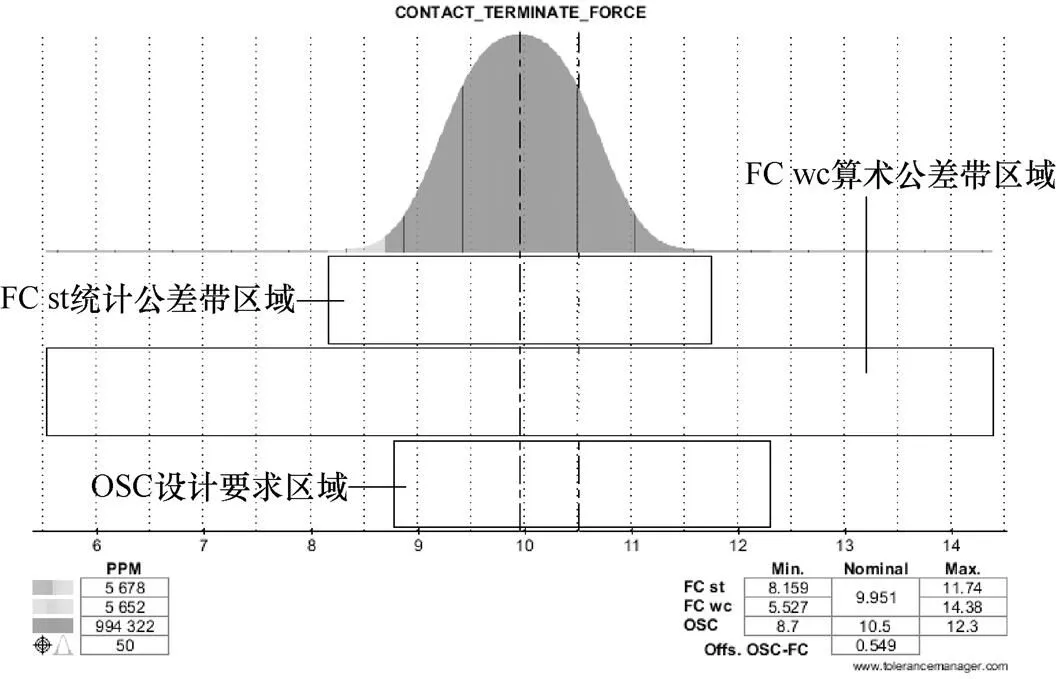
Nominal是名义值

3.3 尺寸链调整与优化

由于触头终压力值是塑壳断路器较为重要的参数指标，故必须适当增加力值，以满足设计要求。

根据初始设计值表1中的敏感度，按绝对值大小重新排列见表2。

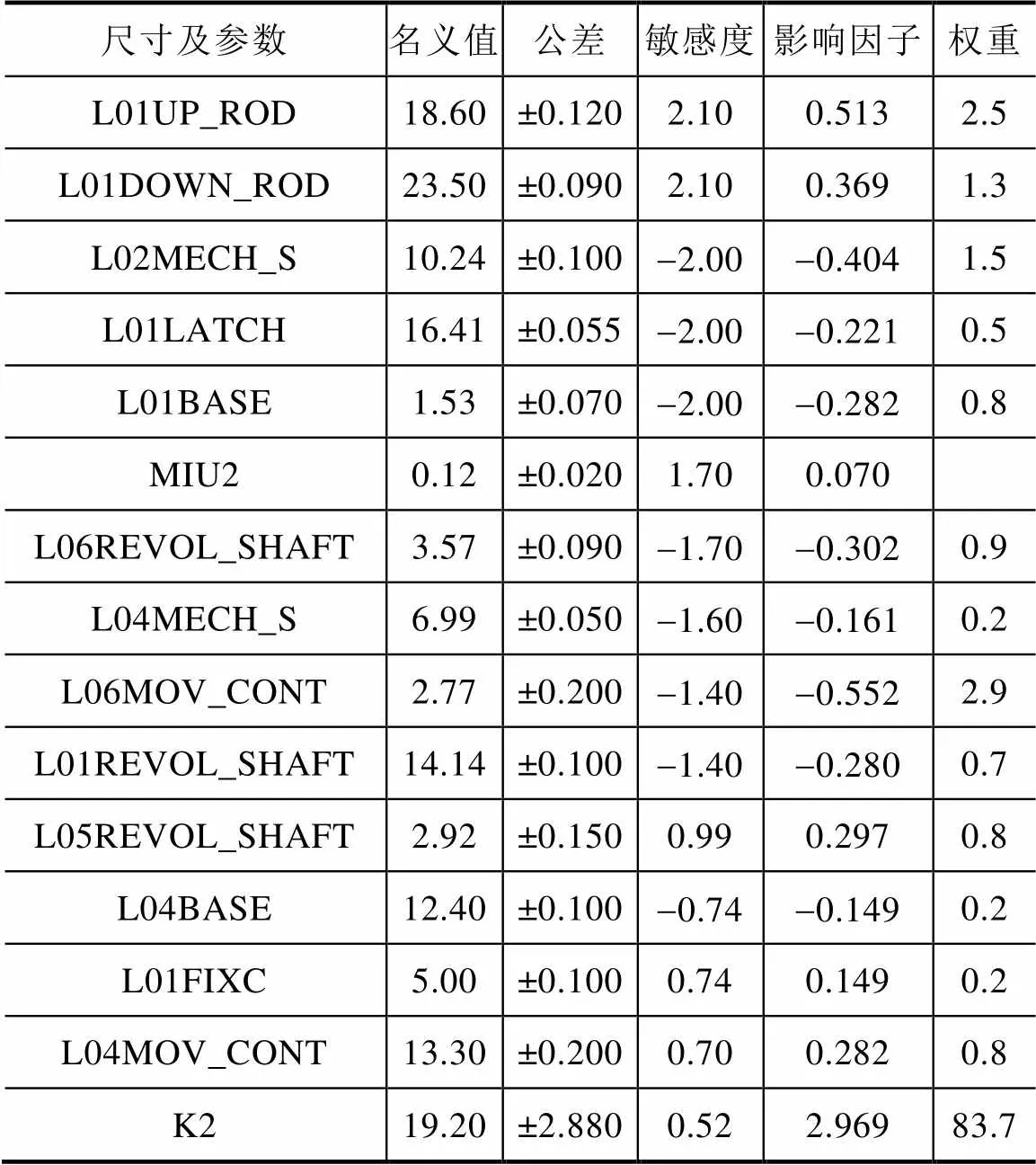
表2 当前尺寸的敏感度大小排列（拣选部分）

从表2中的敏感度值可以知道，对触头终压力值较为敏感的是连杆的孔心距，机构支架的向位置，摩擦因素，跳扣孔心距尺寸。因此，优先调整敏感度大的功能尺寸，调整时应考虑零件的工艺情况、模具情况、借用情况以及是否影响其他功能条件等。文中，首先优化上连杆与下连杆的孔心距。此外，在表2中，还可以看出弹簧刚度系数2的比重很大，因此在连杆调整后，需要酌情对这个参数进行调整，优化前后的尺寸见表3。

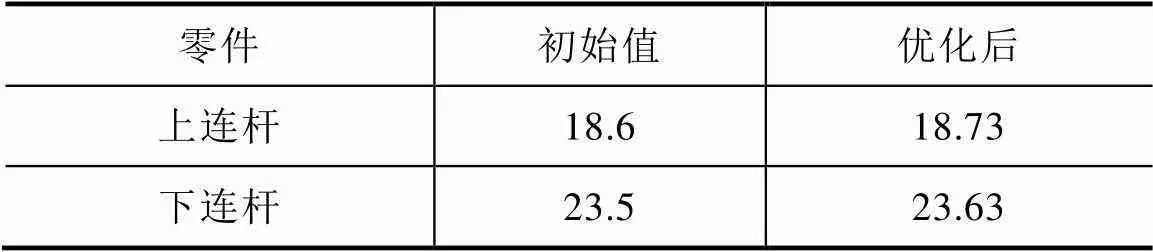
表3 名义值调整

优化后，如表4和图15所示。从图中可以看到，名义值已经符合了，但是公差范围偏大，不良率仍然达到114×10-6，高于设计值50×10-6，此时，不需要调整名义值，而需要某个参数的公差带大小。由表4中可见，弹簧刚度系数2的公差为±2.88，即名义值19.2的偏差比率范围为±15%，因此需要提高弹簧制造精度。

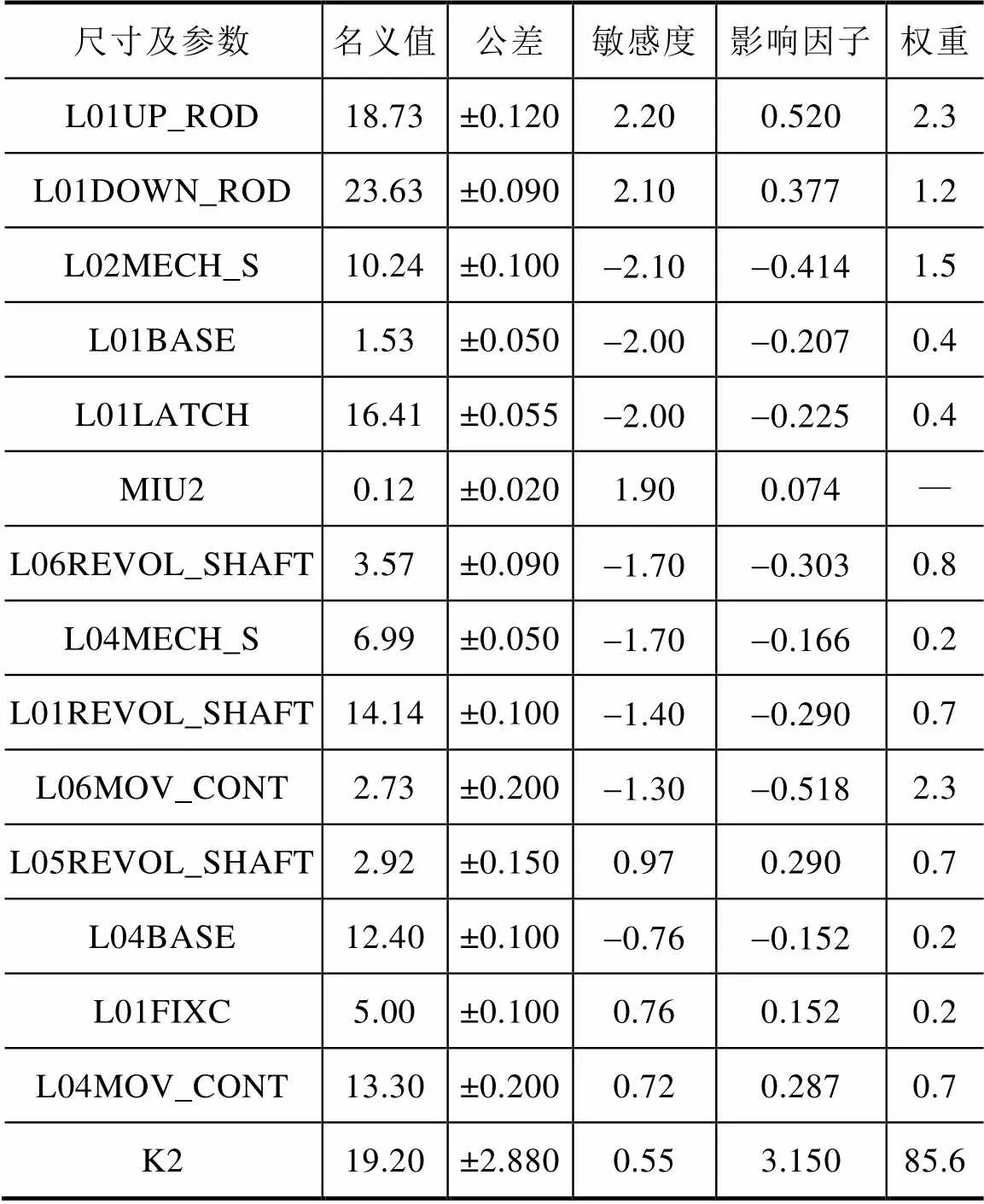
表4 名义值优化后的尺寸表（拣选部分）

上述调整的思想是通过功能尺寸的名义值，将统计公差带中心进行右移，使得触头终压力值增大，达到符合设计要求。

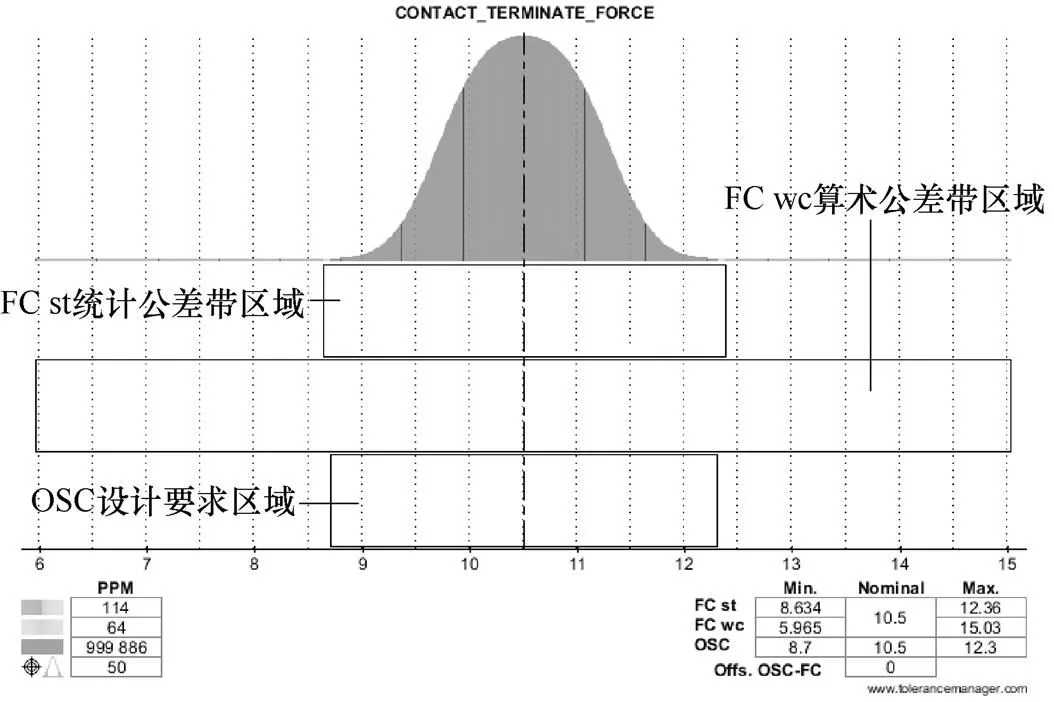
图15 名义值优化后的触头终压力公差分布

因为公差范围还没收紧，所以需要将弹簧刚度系数2的误差比率范围进行优化，控制在±12%以内（即±2.3），结果见表5。可见，此时不良率为2×10-6，小于设计要求50×10-6，合格。当然，优化的值不惟一，公差还可以作适当调整，但余地已经不大。

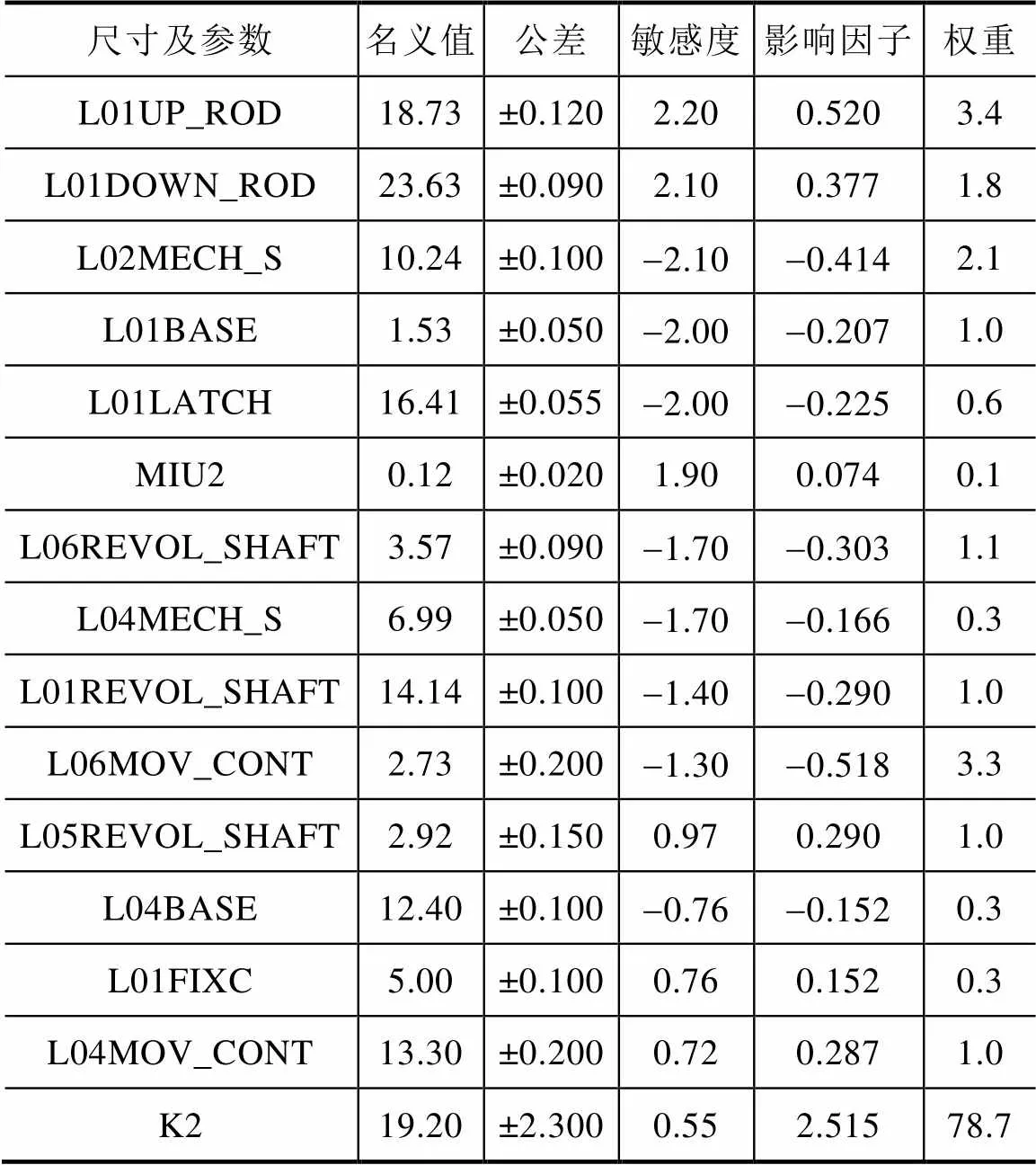
表5 公差调整后的尺寸表（拣选部分）

上述修改的思想是，当名义值满足设计要求时，修改合适的功能尺寸的公差带大小，收紧以符合设计要求。此外，需要说明的是，从图16的FC wc和FC st的范围来看，统计公差（用统计法计算）的范围要比算术公差（用极值法计算）的小，也就是即使相关零部件尺寸及公差都按设计要求做，仍有极小概率可能导致不合格产品事件的发生。当然，若按极值法优化，虽然能够实现完全互换的目标，但对生产成本的增加，则是肯定的。因此，在满足设计要求的前提下，既保证质量，又降低成本是设计师必须做的工作，也是进行尺寸链公差仿真的目的。

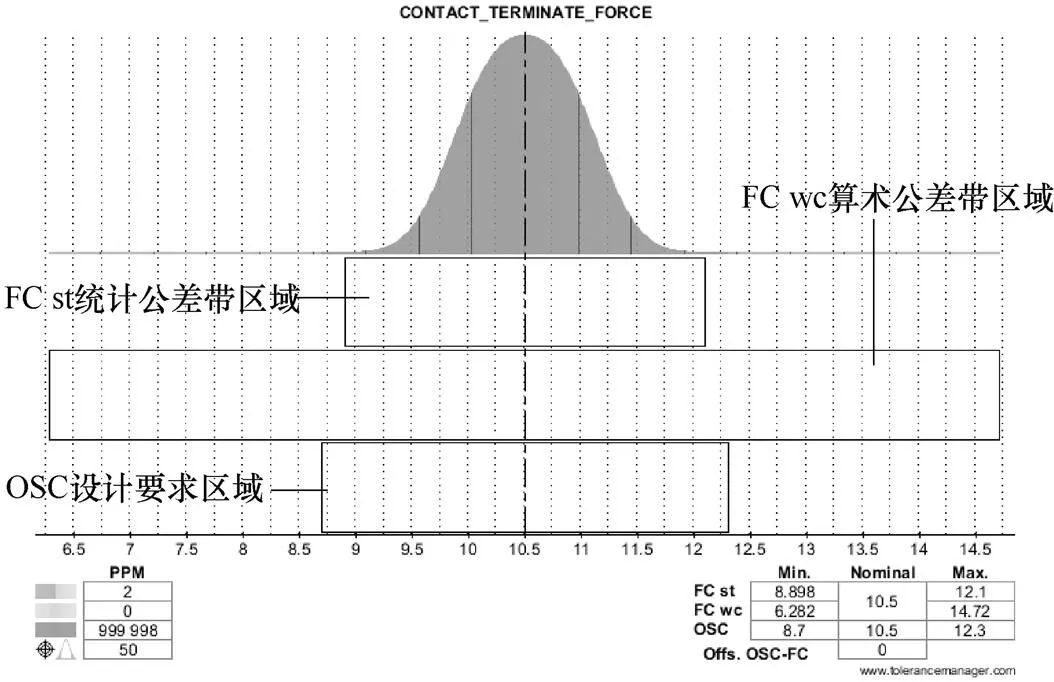
图16 簧刚度误差优化后终压力公差分布

3.4 实测对比

抽样5台产品，测出它的触头终压力，见表6。

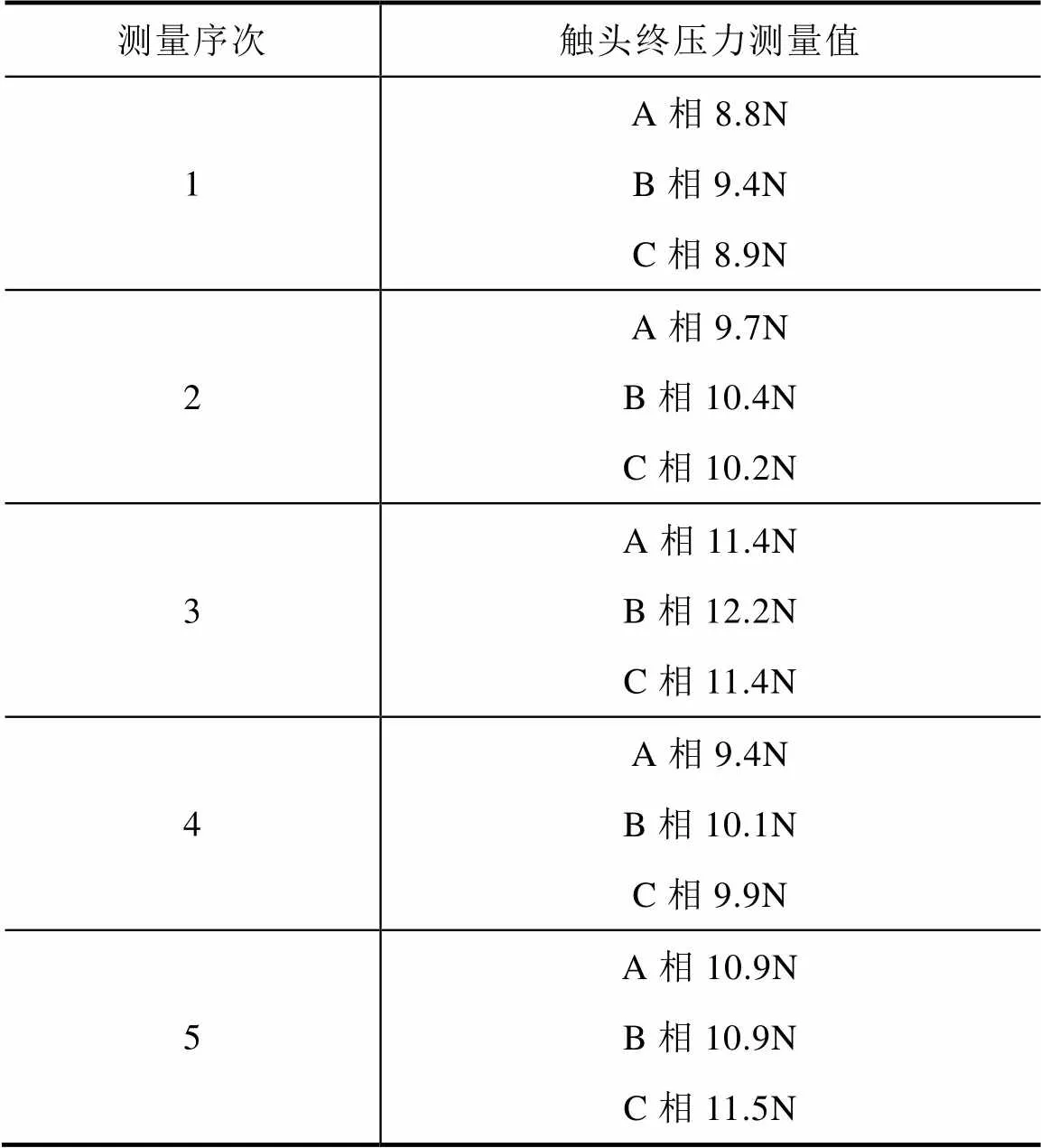
表6 实测量值

通过测量发现，触头终压力的实测值在设计要求允许范围内。统计法计算得到的公差带分布是符合生产实际情况的，在可接受的不良率范围内，能够保证功能条件符合设计要求。有统计数据作为保证，这给设计师提供了有力的理论依据。

4 结论

对制造业而言，借助公差仿真软件进行尺寸链分析，在产品设计、质量控制、问题查找等方面具有非常良好的应用前景。以TM软件为例，其依托良好的人机交互环境，用图形和数字相结合的方式提供设计结果，且结果包含了算术公差与统计公差，与设计要求一起进行对比，直接预测产品量产状态时的合格率。同时，基于草绘模型和静力学平衡模型的前处理，实现了触头终压力尺寸链方程的构建及其公差运算，取代了繁琐的人工求解方法。这款软件综合了微积分、矩阵理论、概率论与数理统计等数学工具，以及参数化和图形化相互驱动的原 理[9]，求解含有静力学参数的非线性尺寸链公差，并结合概率分布，进行公差分配，这是以往人工方法难以企及的。

在优化阶段，按照功能尺寸的敏感度及权重，结合零件的实际工艺情况，按修改零件的成本最小化原则，选择性调整尺寸名义值及公差，使得设计师有了足够的理论依据，也为后续的改进提供了模板。

设计师从本文可以得知，触头终压力与上连杆、下连杆的孔心距、转轴的位置、动触头的位置、操作机构的高度位置以及触头弹簧刚度系数密切相关，弹簧刚度的公差是影响触头终压力公差带宽度的最主要因素。限于篇幅，本文没有罗列其他的功能条件（封闭环）。当多个功能条件同时求解时，设计师会发现，某些功能尺寸对不同的功能条件影响是不同的，这个时候就需要对零件工艺及产品管理方面做一些了解，要联系实际，适当进行取舍，使尺寸链优化有的放矢。有了公差仿真的经历，可以进一步提高设计师对产品的认知水平，抓住产品的关键参数和精髓。

[1] 石振东. 尺寸链理论与应用[M]. 哈尔滨: 黑龙江科学技术出版社, 1993.

[2] 张荣瑞. 尺寸链原理及其应用[M]. 北京: 机械工业出版社, 1986.

[3] 袁亦峰. 塑壳断路器机构静态与动态的稳定性设计[J]. 电气技术, 2013, 14(8): 85-88.

[4] 葛永斌, 杨仕富. 功能设计方法及Tolerance Manager软件在550kV弹簧操作机构设计中的应 用[C]//2013年中国制造业产品创新数字化国际峰会论文集, 2013: 13-24

[5] 秦家爱, 张顺法. 公差分析软件在电气产品设计中的运用[J]. 上海电器技术, 2009(1): 55-59.

[6] 张军化, 徐泽亮, 鲁骞. 计算机辅助公差分析在微型断路器设计中的应用[J]. 低压电器, 2011(10): 53-57.

[7] 赵斐, 汪海贵, 程代玲, 等. 基于TM软件高压真空断路器尺寸链的分析[J]. 新技术新工艺, 2014(3): 57-60.

[8] GB/T 5847—2004. 尺寸链计算方法[S]

[9] 王家海, 周纲. CETOL平台下微型断路器尺寸链及公差研究[J]. 自动化仪表, 2011, 32(9): 14-17.

[10] 孟飙, 王勃. 工程尺寸驱动原理的完善及其在公差分析中的应用[J]. 航空学报, 2014, 35(6): 1740-1749.

[11] 陈佳成. 电器产品机构零部件设计的公差选择[J]. 电气技术, 2014, 15(11): 59-61.

Tolerance simulation analysis of the contact terminate force for molded case circuit breaker

Yuan Yifeng

(Delixi Electric Co., Ltd, Shanghai Branch, Shanghai 201812)

Taking the contact terminate force of molded case circuit breaker as the optimization objective, based on the computer aided tolerance analysis, the stress analysis, dimension sensitivity analysis and weight analysis are introduced to optimize the relative dimension tolerance and the stiffness coefficient of the contact terminate force. The analysis results show that, compared to the previous theory only nominal force value, after considering the stress tolerance analysis, calculation of force not only has theoretical value, but also the tolerance range, and according to the current process, put forward the improvement scheme to optimize the contact terminate force.

molded case circuit breaker; tolerance simulation analysis; contact terminate force

2018-03-19

袁亦峰（1983-），男，浙江慈溪人，本科，工程师，主要从事低压电器仿真技术与尺寸链分析工作。