福州市湿地松人工林树皮厚度模型研究*

严铭海 方静仪 李睿宇 江希钿

(福建农林大学林学院，福建 福州 350002)

树皮厚度受每个树种的遗传因子控制，导致不同树种的树皮厚度往往有差异[1]。Zeibig-Kichas等[2]对加利福尼亚针阔混交林中8种针叶树的树皮厚度进行了研究，发现不同针叶树种之间差异大，8种针叶树中树皮厚度最大的是北美翠柏 (Calocedrusdecurrens)，最小的是美国黑松 (Pinuscontorta)。树皮厚度在树种间变化很大，但一般随直径的增加而增加[3]。有研究结果显示，直径每增加10 cm，树皮厚度约增加1.2 mm[4]。同一树干不同高度对应的直径往往不同，导致树皮厚度也随之变化。Laasasenaho等[5]也认为树皮厚度不仅取决于树种，同时也和树干的不同高度位置密切相关。还有研究表明，针叶树比常绿阔叶树种具有更大的树皮厚度[6]。

国内外学者对树皮厚度进行研究，得出了许多计算树皮厚度的数学模型。其中，胸径通常作为一个很重要的解释变量，此外树高和年龄等变量的加入，也取得了较好的拟合效果[7-10]。但同一树干的不同位置，树皮厚度往往不一样，因此任意树干高度的树皮厚度方程被建立[11-13]。除此之外，相对树皮厚度的方程也被一些学者用来计算树皮厚度[12-14]。较常见的还有去皮直径模型，在求不同高度的树皮厚度时也很方便[15-17]。

湿地松 (Pinuselliottii) 原产于美国东南部，我国从20世纪30年代开始引种，因其具有速生、适应性强、木材用途广和松脂产量高等优良特性，现已成为亚热带地区大面积造林树种，是我国引种的优良速生树种之一[18-19]。湿地松的树皮有不同于松脂的浓厚香味，其树皮提取物不仅可以用于制备改性酚醛树脂胶和胶合剂，还具有治疗平喘的药理作用[20-21]。目前我国湿地松人工林种植面积超过300万hm2[22]，木材和树皮资源量巨大。研究湿地松树皮厚度模型对于木材和树皮资源的生产利用都非常重要，但目前还缺少合适的模型来预估湿地松树皮厚度。基于此，本研究通过收集前人构建的模型和自建模型，应用前期湿地松样木获取的带皮直径 (dob)、去皮直径 (dib)、树皮厚度等数据对模型进行拟合，对比分析不同模型的拟合效果，并筛选出各类树皮厚度预测的合理模型，从而为湿地松材积、出材率和树皮生长量的估测提供参考。

1 研究区概况

研究区为福建省福州市，位于福建省中部东端、闽江下游，全市面积11 968 km2。地处北纬25°15′～26°39′，东经118°08′～120°31′，海拔600～1 000 m。该市属于典型的亚热带季风气候，温暖湿润，雨量充沛，阳光充足，无霜期326 d，年均日照数1 700～1 980 h，年均温20～25 ℃，年均降雨量900～2 100 mm。湿地松是当地重要的造林树种。

2 研究方法

2.1 数据采集

结合伐区木材生产，在福州市湿地松人工林中设置标准地共87块，考虑不同的海拔 (h)、坡度 (s)、郁闭度 (c)、林分年龄 (t)、胸径 (DBH)、树高 (H) 等因素，从标准地中随机抽取217株样木，其所在标准地基本信息详见表1。伐倒样木之后，用皮尺 (精度为0.01 m) 测量全树高和冠长，然后再以1 m为间隔，于树干上0.3、0.5、1.3、1.5、2.5 m等位置处，用钢卷尺 (精度为0.1 cm) 依次读取带皮直径和去皮直径 (剥除树皮后读取)，并计算树皮厚度。

表1 样木所在标准地基本信息Table 1 Information of sample plots

由于需要考虑模型的拟合和验证，故将217株样木按75%和25%的比例随机分为两部分，一部分用于建模 (样木163 株)，一部分用于模型检验 (样木54 株)，样木数据的描述性统计结果见表2。模型变量包括林分年龄、树高、胸径、胸高处树皮厚度 (BBT)、任意树高处树皮率 (z)、相对树皮厚度 (RBT)、树冠率 (CR)、树冠长 (CL)，其中任意树高处树皮率为该处去皮直径与该处带皮直径之比。

2.2 模型形式

通过查阅资料，参考前人建立的14个模型，再加上自行构建的4个模型，共获取18个模型用于本研究，具体模型见表3。树皮模型的分类采用唐诚等[13]的研究结果，依据模型因变量将其归纳为4种。

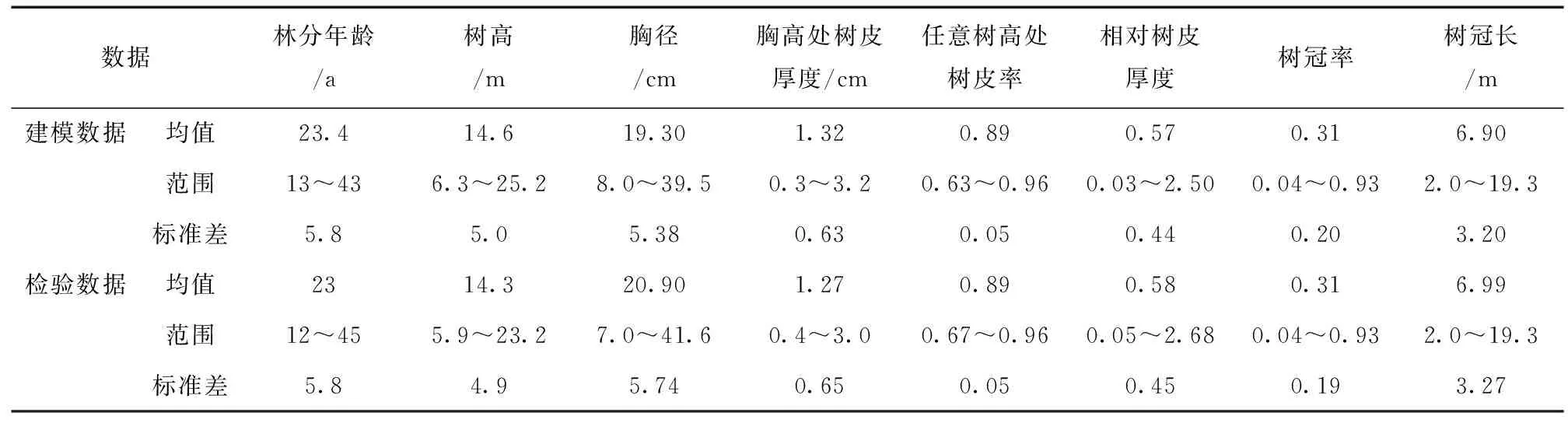
表2 湿地松人工林树皮厚度建模和检验数据Table 2 Fitting and validating data for bark thickness models of P.elliottii plantations

表3 模型形式Table 3 The models form

注：各模型中，BT表示任意高度处树皮厚度；RD表示相对直径；RH表示相对树高；a表示常数；B1、B2、B3表示模型参数。

2.3 模型质量评价指标

4类树皮厚度模型均采用最小二乘法进行拟合，并对模型参数进行显著性检验，满足所有参数均显著的模型，进一步计算赤池信息准则 (AIC)、交叉验证误差 (CVE)、偏差 (B)、绝对偏差 (AB)、决定系数 (R2) 作为模型质量评价的5个指标，其计算方法分别见公式 (1)～(5)。

(1)

(2)

(3)

AIC=-2lnζ+2p

(4)

(5)

在计算交叉验证误差时，将建模数据分为没有重叠的k份 (k=5)[23]。用k-1份去拟合模型，用第k份进行检验，这个过程重复k次，直到每一部分都被抽出做一次模型检验，做k-1次模型拟合，计算k次均方误差 (MSE) 的平均值即得到交叉验证误差值。在R软件中，CVE通过cv.glm函数计算得到。

2.4 模型优选方法

应用相对排序法[24]进行模型优选，分别计算各模型AIC、B、AB、CVE和R2的相对排序值，其计算方法见公式 (6)。

(6)

式中：Ranki为模型i的相对排序值 (i=1, 2, …,w)，其值越小说明模型拟合效果越好；w为参与排序的模型数目;Si为模型i的统计指标值 (分别为AIC、B、AB、CVE和R2)；Smin和Smax分别为Si的最小值和最大值。

偏差均值和AIC都存在有负值，但偏差需取绝对值来计算排序值，而AIC是无论正负，越小越好，故可直接参与排序。对于R2则是越大越好，为了统一越小越好的标准，将1-R2作为排序的统计指标值。最后求出5个统计指标的平均相对排序值，通过比较其大小可判断模型质量的优劣，并筛选出最优模型。

2.5 模型检验方法

对最优模型进行配对t检验来判断预估值和实际值之间差异是否显著，若差异不显著，则说明模型有效性良好。进一步通过方差扩大因子法对其进行多重共线性的诊断，再通过怀特检测其是否存在异方差，如果有明显异方差的模型，则可通过变量变换进行修正[25]。

3 结果与分析

3.1 模型拟合参数检验

以217株样木的相关数据为依托，对18个模型进行拟合，其参数显著性检验结果 (表4) 表明：模型2、5和11均有一个参数预估值与零差异不显著，将不参与进一步分析。分析结果可以看出模型2、5、11中不显著的都是H或lnH的参数，这与唐诚等[13]的研究结果一致。

3.2 模型拟合质量评价

模型拟合质量好坏很大程度上影响着预估的精度，模型统计指标计算及排序见表5。

表4 模型参数及其显著性检验Table 4 Model parameters and its significance test

注：*和ns分别表示模型参数预估值在5%水平与零差异显著和不显著。

表5 模型统计指标计算及排序Table 5 Model statistical index calculation and ranking

模型B值相对排序值AB值相对排序值CVE值相对排序值AIC值相对排序值1-R2值相对排序值相对排序值均值10.000 1.001 0.437 11.408 0.331 1.005 249.161 4.402 0.640 14.000 6.363 30.094 12.293 0.442 11.574 0.208 1.003 186.095 4.379 0.552 12.211 8.292 40.091 11.989 0.443 11.602 0.204 1.003 183.141 4.378 0.534 11.836 8.161 60.108 14.000 0.285 6.445 0.126 1.002 2055.314 5.078 0.375 8.591 7.023 70.093 12.194 0.281 6.320 0.107 1.001 1619.298 4.915 0.318 7.436 6.373 8-0.0001.000 0.229 4.636 0.093 1.001 1246.407 4.775 0.277 6.596 3.60290.000 1.000 0.237 4.884 0.096 1.001 1338.884 4.810 0.286 6.794 3.698 10-0.0001.000 0.227 4.567 0.091 1.001 1174.355 4.748 0.269 6.445 3.552 120.000 1.000 0.108 0.661 0.025 1.000 -2315.266 3.443 0.226 5.563 2.333 130.0001.000 0.118 1.000 0.027 1.000 -2082.532 3.530 0.246 5.981 2.502 140.000 1.000 0.125 1.222 0.032 1.000 -1659.435 3.688 0.288 6.835 2.749 150.021 3.524 0.516 14.000 0.505 1.007 5781.896 6.472 0.002 1.000 5.201 16-0.0001.000 0.508 13.718 0.504 1.007 5771.969 6.468 0.011 1.181 4.675 17-0.043-4.159 0.509 13.773 928.422 14.000 25908.153 14.000 0.008 1.122 7.747 180.003 1.414 0.508 13.736 0.002 1.000 -8846.419 1.000 0.007 1.096 3.649

由表5可知，14个模型中6、7、3和4的偏差值最大，接近于0.1，模型17和15的偏差值为-0.043和0.021，其余9个模型的偏差值均接近于0。拟合去皮直径的4个模型绝对偏差最大，约为0.51；其次是拟合胸高处树皮厚度的3个模型，约为0.44；拟合任意树高处树皮厚度的模型中，模型6和7的绝对偏差最大，其余的模型8、9、10约为0.23；拟合相对树皮厚度的模型绝对偏差最小。模型18的CVE值最小，模型17的CVE最大，剩余模型中CVE最大的是去皮直径模型；相对树皮厚度CVE模型最小，任意树高处树皮厚度模型的CVE值在0.1附近，胸高处树皮厚度CVE值约在0.2～0.3。AIC的排序情况和CVE基本一致。R2以模型15、16、17、18为最高，均接近1。而模型1、3、4的R2则在0.5以下。

从5项指标的综合排序值可以看出，模型3、4、6、7、17的排序值较高，模型12、13、14的综合排序值较低，其他模型居中。同形式模型进行比较，胸高处树皮厚度的3个模型中，模型1拟合质量最好，模型4最差。任意树高处树皮厚度的5个模型中，模型10拟合效果最好，模型6最差。相对树皮厚度的3个模型中，模型12的拟合质量最好，模型15的拟合质量最差。去皮直径的4个模型中，模型18的拟合质量最优，模型17最差。由此筛选出较优模型为1、10、12、18。

3.3 模型检验

运用54株样木的相关数据对最优模型进行配对t检验，模型1、10、12、18的预估值和实际值之间没有显著差异 (表6)。进一步对其进行多重共线性诊断和异方差分析 (图1)。

表6 模型配对t检验Table 6 t test for model paired

图14个模型残差
Fig.1 Residuals of 4 selected models

4个最优模型中的模型1、12、18均只有1个自变量，故不需要考虑共线性问题。而模型10则用方差扩大因子法分析其共线性，其3个自变量的VIF值分别为1.079、2.414、2.361，均小于10，认为模型10的各自变量不存在严重的多重共线性。

从4个模型的残差图 (图1) 可以看出，模型1和12的残差分布均匀且随机，经过怀特检验表明模型1、12不存在异方差，模型10和18则有异方差问题，故通过取对数后回归。变换后模型的残差图 (图2) 和评价指标 (表7) 均有改善。

图2异方差修正后模型残差
Fig.2 Residuals against fitted values for 5 models after correction of heteroskedasticity

表7 原模型与变换后模型统计指标对比Table 7 Statistics indices comparison between the original models and changed models

4 结论与讨论

本研究通过5个评价指标筛选出模型1、10、12和18，分别用于拟合胸高处树皮厚度、任意树高处树皮厚度、相对树皮厚度、任意高度去皮直径，4个模型拟合精度高，不存在多重共线性问题，且模型没有异方差或经过变量变换得到较好的修正。拟合模型所需的数据除了冠长率之外，其余数据在林业生产实践中具有易获取性。在树皮厚度模型中加入冠长率，对于湿地松而言，拟合效果较好。

胸径是拟合胸径处树皮厚度模型的重要自变量，此外，再通过增加一些自变量也可以提高模型的决定系数。本研究中的模型2、4、5增加了自变量树高或年龄，然而因为胸高处树皮厚度与树高不相关，导致模型2、5的参数检验不显著。模型3、4是在模型1的基础上通过变量的对数变换后得到，可以看出其决定系数明显提高，但模型3的实际值和预测值差异显著。剩余的模型中，从模型质量指标综合排序来看，模型1的拟合效果优于模型4。

王晓林等[9]对落叶松的研究中发现，树皮厚度与冠长和冠长率存在着一定相关性，但无法确保其对树皮厚度有显著影响。因此本研究在任意高度处树皮厚度的模型中考虑了冠长和冠长率2个自变量，在模型8中新加入了自变量冠长，模型9和10中新加入了自变量冠长率，结果发现模型参数检验均显著并且决定系数均提高至0.7以上。任意高度的带皮直径是模拟任意高度处树皮厚度的重要解释变量，模型7、8、9、10在模型6的基础上陆续加入RH、CL、CR和RD等自变量，拟合效果均有改善。经过比较模型质量的综合排序值，认为模型10拟合效果优于模型6、7、8和9。

鉴于冠长率在模型10中取得良好的拟合效果，因此尝试在模型14的自变量中增加冠长率，与其他相对树皮厚度模型相比，模型14虽然参数检验显著，但相比较而言决定系数较低。模型11也因为自变量有树高，导致模型参数与零相比不显著。在拟合相对树皮厚度时，有学者认为模型12中的B2会因树种差异而不固定[16,25]。Johnson等[14]对辐射松 (Pinusradiata) 的研究发现，B2赋值4.0时拟合效果良好；唐诚等[13]对西南桦 (Betulaalnoides) 的研究表明，B2赋值约1.0时效果最好；对于湿地松而言，B2约1.7时拟合效果最佳。比较同类模型的综合排序值，模型 12的拟合效果略优于模型13、14。

任意树高的去皮直径在森林经营和木材加工过程中非常重要，Marshall等[26]研究发现去皮直径的预测误差会导致高达11%的木材价值损失,同时去皮直径也是木材企业生产时关心的问题。去皮直径主要通过带皮直径来拟合，本研究中用来拟合去皮直径模型的R2都接近1。模型15的B1常称为树皮因子，模型17是在模型15的基础上对变量进行平方变换来的。模型16和模型18分别在模型15的基础上增加常数项和参数B2。综合比较各统计指标值，认为模型18的拟合效果最佳。

树皮厚度除受直径、冠长、冠幅、树高、年龄等因子的影响外，还可能受生长速率的影响。有学者的研究表明，不同树种的生长速率往往不同，生长较快的树种一般树皮略薄[2]。Stängle等[27]对德国西南部云杉 (Piceaasperata) 树皮厚度估测模型的研究中，发现立地条件对树皮厚度的影响很大，立地质量较好，相对应的树皮厚度较小。立地质量有时也会影响树木的生长速率，同时也是影响树皮厚度的重要因素。但本研究中未考虑立地因子，在往后的研究可以尝试加入立地因子来提高模型精度。目前，树皮厚度方面的林业数表很少，如果有条件可基于树皮模型的研究构建相对应的林业数表，也是对林业数表的一种补充。此外，树皮厚度在森林动态模拟中的其他方面应用，还有待深入研究。