贝叶斯分类模型在学生成绩预测中的应用研究

韩丽娜

（咸阳师范学院图形图像研究所 咸阳 712000）

1 引言

贝叶斯分类方法是一种基于统计的学习方法，它利用概率统计进行学习分类，如预测一个数据对象属于某个类别的概率，主要算法有朴素贝叶斯分类算法，贝叶斯信念网络分类算法等。贝叶斯分类方法能够充分利用领域知识和先验信息，显示计算假设概率，而且分类结果是领域知识和数据样本信息的综合体现［1～2］。随着信息化技术的不断发展，高校积累了大量的学生信息，因此希望通过建立贝叶斯分类模型对已有学生数据进行挖掘分析，预测学生成绩分布情况，及时反馈教学效果，进而对学生的行为进行个性化指导，不仅有利于教师改进教学方式，而且对学生的管理工作也提供了有用的参考信息。因此应用贝叶斯分类模型进行学生成绩分析具有重要的现实意义。

2 贝叶斯分类模型理论

2.1 贝叶斯定理

贝叶斯方法采用计算每一个样本属于每一类的概率，然后将样本划分为具有最大概率的那一类中。即已知样本x的条件下，计算其属于某一类的概率［1～3］。

2.2 贝叶斯公式中的相关概率

先验概率P(cj)：表示训练样本数据前cj(类别)拥有的初始概率。P(cj)常被称为cj的先验概率（prior probability）［4～5］，通常采用用样例中属于 cj的样例数 ||cj与总样例数 ||D 的比值来近似表示［2～3］。如式（1）所示：

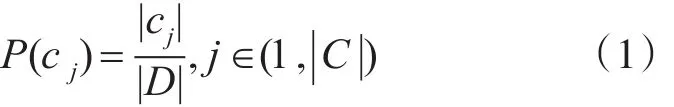
类条件概率（似然概率）P(X | cj)：指当已知类别为 cj的条件下，出现所考察样本 X 的概率［4，6］，若设 X=a1,a1,…,am，则如式（2）所示：

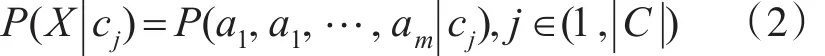
后验概率P(|cjX)：指当给定数据样本 X，属于cj类的概率。P(|cjX)被称为cj的后验概率（posterior probability），它反映先看到数据样本 X后 cj成立的置信度［4，7～8］。使用贝叶斯公式计算后验概率，如式（3）所示。

贝叶斯公式：

由于P(X)对所有类都是相同的，因此在实际的应用中我们只需计算贝叶斯公式分子部分，求取最大值［8～9］，如式（4）所示，然后把X就分到最大值对应的类ccmp中。

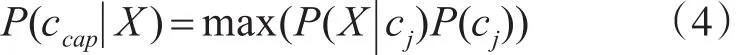
2.3 朴素贝叶斯分类器

由于计算式（2）相当困难，所以朴素贝叶斯分类器假设：在给定样本的目标值时属性之间的相互条件独立。即式（2）求取的类条件概率就是每个单独属性对应的概率的乘积［3～4，10］，如式（5）所示。

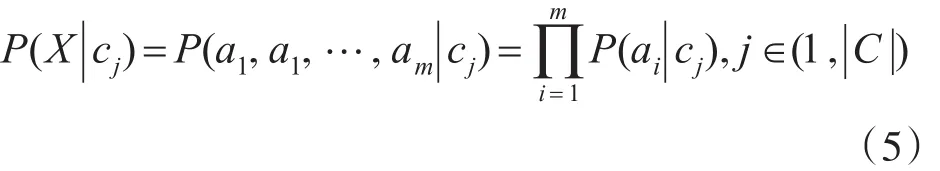
因此，对于朴素贝叶斯学习方法就是从训练样本中估计不同的P(cj)和P(ai|cj)，针对新的待分样本实例，采用式（4）、式（5）进行计算给出分类结果。

2.4 应用贝叶斯分类模型预测学生成绩

2.4.1 数据准备

Characteristics of Ship Domain in Typical Inland Waters

本次数据信息以某学院某专业38名同学《程序设计基础》期末上机考试成绩为基础，结合学生的平时成绩（考勤，回答问题，作业完成）以及学生的调查数据信息（课程的兴趣，每周上机时长，试卷难易程度，学生自评）等对学生信息采用贝叶斯分类模型进行数据挖掘分析［11～12］。训练样本有23个数据，属性有3个，包括考勤，上机时长，课程兴趣［13］。如表1所示。

表1 23个训练样本

2.4.2 求解先验概率和类条件概率

表2 类别为cj及在cj条件下Ai取ai的样本数统计

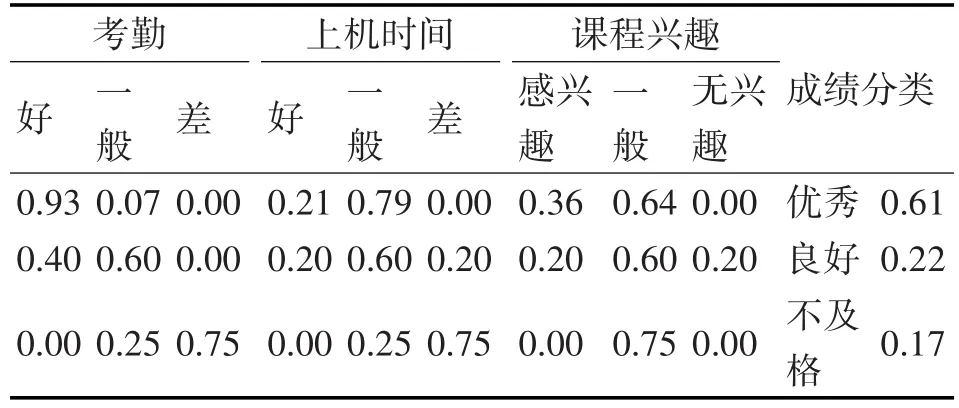
表3 先验概率P(cj)和条件概率P(ai|cj)

2.4.3 贝叶斯模型的应用

现在假设有一学生样例，统计他的3个属性：考勤，上机时长，课程兴趣，具体的取值为X={ }

一般，一般，一般 ，预测该学生成绩的分类情况。

根据贝叶斯式（4）、（5）：

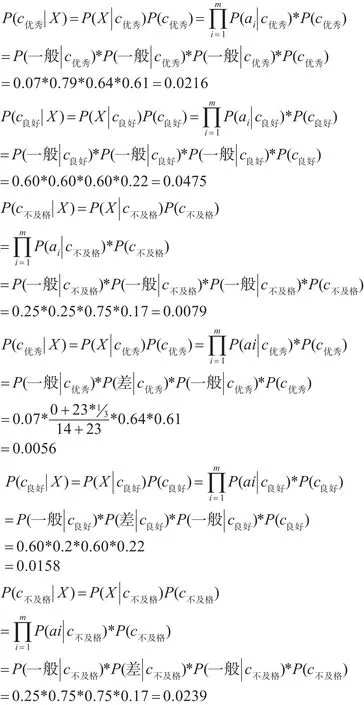
在表3对样本计算条件概率时，一般情况下它是对其真实概率的一个良好估计，但我们发现有包含第i个属性的取值ai时，它的条件概率值为0，如果待估样例中属性取值为ai的话（条件概率为0），那么贝叶斯公式整个的结果即为0。

例如，我们将样例改为 X={一般,差,一般}，那么计算的后验概率中有1个值为0。为了更加准确地计算条件概率，可以采用m-估计来解决这个问题［13～15］。它的含义是将 nj个实际观察扩大，加上m个按Pi分布的虚拟样本，其中m是等效样本大

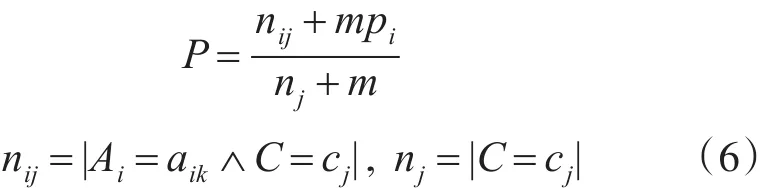
因此，对于样例 X={ }一般，差，一般 ，采用式（6）重新计算条件概率和后验概率。

因此，P(ccap|X)=max(0.0056,0.0158,0.0239)=0.0239，所以预测该学生的分类为不及格。与前期采用决策树算法进行成绩分析的结果一致［13］。

2.4.4 模型评估

基于23个训练样本，采用贝叶斯分类模型进行某班学生学习成绩的预测分类，是否对其它样本集有效呢？将12个测试样本数据按照此贝叶斯模型重新计算分析，10个学生数据符合模型的结果，准确率达到了83%。采用其它类似专业同门课程的学生信息数据进行测试，准确率也达到了80%以上，因此该模型是有效的。通过对学生成绩的预测分析，我们可以看到，考勤差的学生成绩预测基本为不及格，考勤较好的同学不管对课程是否感兴趣成绩预测基本都是良好以上，上机时长对学生的影响不大，这与学生、课程性质都有关系，值得代课教师好好深思，进而为以后的教学工作起到指导作用。贝叶斯分类模型意义比较明确，便于理解，它的时间复杂度低，可以应用大型数据库，而且易于实现增量。

3 结语

文章论述了贝叶斯模型的基本理论，采用贝叶斯分类器对学生成绩问题进行了分析研究。选取影响学生学习成绩的主要因素作为属性，通过使用训练样本计算出先验概率和类条件概率，然后对待测样本数据进行计算。通过分析，学生考勤是影响学生成绩的主要因素，说明上课听讲对学生掌握本门课程是非常重要的。通过使用样本数据对模型进行测试评估，准确率达到了83%。不足之处该模型中样本数据较少，考虑影响学生成绩的因素不够全面，而且贝叶斯分类模型需要知道先验概率，并假设属性之间相互独立，因此当属性个数较多或属性之间相关性较大时，分类效率比不上决策树模型。