动态旅游行程规划的标签校正算法
2018-10-23荆怀芳
荆怀芳
(咸阳职业技术学院财经学院 咸阳 712000)
1 引言
近年来,中国举办了APEC峰会,多种商业展览等多种观光和展览活动,但很多游客在一个或多个日子里访问了一个地区或城市[1]。到处游览是不可能的,游客想要选择他们认为最有吸引力的兴趣点(POI)[2]。他们的选择可以根据网站的信息,杂志上的文章或书店中的指南来进行。一旦做出决定,游客将决定访问每个点的时间并选择点之间的路线。然而由于许多因素,例如许多地方拥挤,交通事故可能发生或道路正在建设中或关闭,这些将导致旅行计划的不确定性[3],因此游客难以设计时间表。游客的目标是在有限的时间内尽可能多地访问POI的旅行计划。以往的研究大多是在静态网络中解决旅游行程问题,这将不可避免地造成不合理的结果[4~6],基于静态网络的传统旅游行程设计已经不能满足日益增长的行程规划需求。综合移动和感知技术并考虑到实时交通信息,建立基于动态网络的旅行者出行设计才能为游客提供个性化和高质量的服务。
目前,旅游行程设计问题(TTDP)常被视为定向问题(OP)的延伸[7]。OP也被称为选择性旅行销售员问题(STSP)[8],背包问题[9],最大收集问题(MCP)[10]和银行劫匪问题[11]。此外,OP可以归结为资源受限TSP问题的特例(RCTSP)[12]。由于这些问题都是NP难题,大多数研究集中利用启发式算法,例如引导式局部搜索[13],蚁群算法[14]等。动态行程设计主要依靠移动通信技术来提供基于旅游位置的实时快速导航服务。同时,它还可以帮助游客选择目标点并找到到达目的地的最短路线。这类移动导航包括百度地图,高德地图和谷歌地图等[15]。然而,随着生活质量和审美情趣的不断提高,游客的喜好也随之变化。静态行程设计不考虑游客的具体情况,例如,旅游者的开始和结束访问时间,当前时间,预期总时间和天气状况等。因此,基于情境和位置的个性化移动导航成为必然趋势。文献[16]设计了一个动态性的旅游指南来决定在一段时间内参观一座城市,通过语义匹配算法接收兴趣匹配点。文献[17]提出了移动导游个性化的旅游行程设计算法。通过结合人工智能和引导式本地搜索启发式方法,为使用移动设备的游客提供快速决策支持。
上述研究只是在基于起点,终点和预算时间内的静态网络研究TTDP,而不涉及动态时变网络中的旅游行程设计问题。旅游出行网络在实际中是依赖展览或旅游时间。例如,展览中高峰时间和低谷时间的旅游时间差异显着。随着先进的传感器网络,信息系统和数据库的发展,在旅游行程规划中融入动态交通信息是有效提升用户个性化需求的方式。因此,在研究时变网络中制定旅游出行问题时,本文在时间聚合图的基础上提出了一种数学规划模型,并建立了一种标签校正算法(LCA)来解决动态旅游行程设计问题。
2 问题描述
2.1 问题假设
时变网络中的旅游出行设计问题可以表示为给定一组访问点和游客偏好值,每个访问点都有一个平均停留时间且每个访问点只能访问一次。这个问题的目标是如何决定访问每个点的时间并选择点之间的路线,以最大限度地在给定的预算时间内提高游客旅行的总效用,即所有选择的访问点的偏好值的总和。本文将基于以下假设解决时变网络中的旅游出行设计问题:
假设1:在时变网络中,边缘上的旅行时间取决于进入的时间,即一旦进入边缘,旅行时间由进入的起始时间给定。
假设2:游客对每个访问点都有一个优先值,它被设定为一个随机整数。这个数值代表游客对这一点的兴趣。在实际应用中,利用移动导航设备的信息检索或语义识别技术来获得该偏好值。
假设3:游客根据时间表决定行程计划,确定预算时间是固定不变的。
假设4:一般来说,一个旅游者不止一次去旅游点,所以每一个景点最多只能被访问一次。
假设5:不考虑旅行道路上的返程和回合现象。
假设6:考虑到交通传感器网络,信息系统和数据库的广泛使用,离散时间的旅行时间被设置为动态且可用的。
2.2 时间聚合网络
给定网络G=(V,E),其中V={V,i=1,2,…,n)是节点集,E={eij|Vi,Vj∈V)是边缘集,如果Vi与Vj相邻,则存在一个边eij在它们之间,|E|=m。由于边缘和边缘上的旅行时间是时变的,则不容易在每个边缘上表示游客移动。因此,使用时间聚合图来表示每个时刻的网络变化[18]。
在时间聚合图中,每个弧具有两个属性:时间序列ETij表示它们出现的时间点,而旅行时间序列TTij表示各个时刻的旅行时间。ETij=[1,2,…,T]代表每一时刻弧线的存在状态,且弧线连接时的一组对应时间表示网络拓扑随时间变化。旅行时间序列TTij=(Tij(1),Tij(2),…,Tij(T))表示边缘存在时的旅行时间,Tij(t)表示当入场时间是t时边缘eij上的旅行时间。如果边缘eij在时间t时没有入场,则Tij(t)=∞,这意味着该边缘不能通过并且必须等待。例如,在时刻t=1,2,3时的时变网络如图1所示。
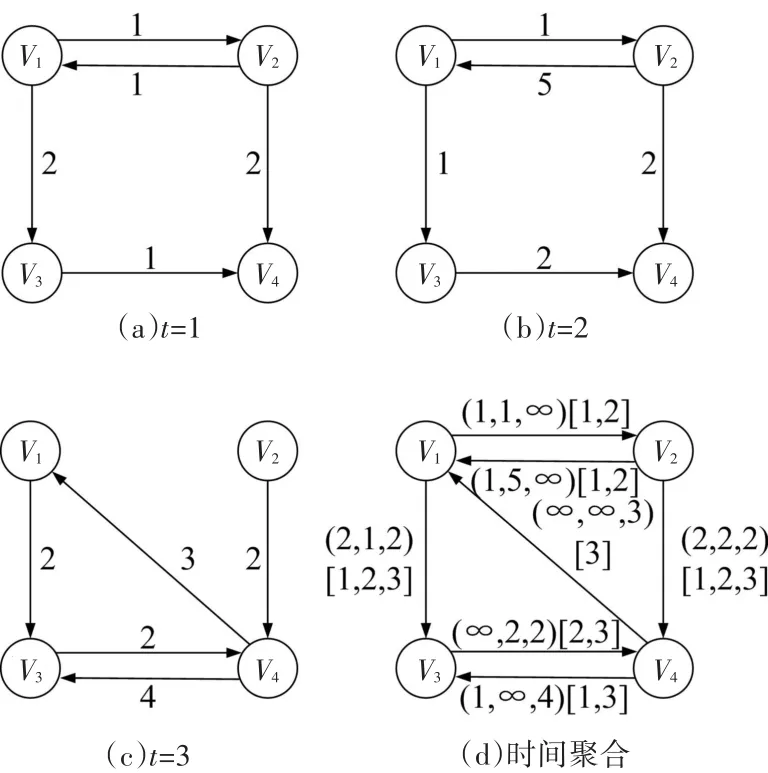
图1 基于时间聚合图的时间相关网络
该网络的拓扑结构和传播时间随时间而变化。对于边缘e21,其在时间t=1,2处出现,但在时间t=3处消失,即不通过。此外,边缘e21的行进时间在时间t=1时等于1,并且在时间t=2时等于5。这个时间聚合图如图1(d)所示,其中边e21有两个序列属性:[1,2]表示边存在时的时间序列,行程时间序列(1.5,∞)表示在时刻1和2的旅行时间。
2.3 旅行演示
在时变网络中,游客旅行利用时间和空间维度来刻画,其中,时间可描述为离散单位,空间可表示为V={Vi|i∈[1,|V|]}。因此,旅游行程可以表示为包含元素Vi(ti)的列表,其中,Vi(ti)表示在ti时刻到达节点Vi。即旅游行程表示为P(V1,Vn)={V1(t1),…,Vn(tn)},其中,V1是源节点,Vn是目地节点。根据时间聚合图原理,如果节点Vi处的停留时间为vti,则边缘eij处的最早到达时间为te=min{t|t≥ti+vti,t∈ETij}。 对于边缘 eij上的两个节点Vi(ti)和Vj(tj),时间约束表示为tj=ti+vti+Tij(te)。
2.4 数学模型
模型问题的目标是最大化总效用,建立如下的混合整数规划:

游客的流量守恒约束为
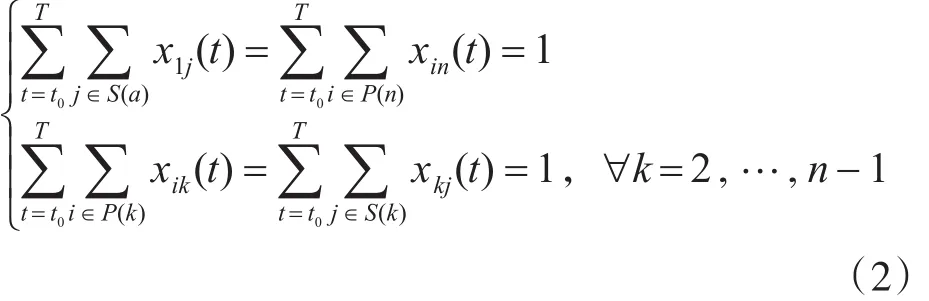
确保每个点最多访问一次:

在给定的旅行中,如果一个边缘被访问,那么沿着节点的边到达时间就是先前到达时间,访问时间和边缘旅行时间的总和。

约束开始时间和结束时间:

约束变量:

其中,G=(V,E)代表时变网络,P(i)和S(i)分别表示节点Vi的前驱节点集合和后继节点集合,T表示旅行的总时间预算,t0表示旅行开始时间,pi,vti和ti分别表示节点Vi的旅游偏好值、停留时间和到达时间,矩阵tij(t)表示在入场时间为t时的边缘eij上的行程时间:

3 标签校正算法
3.1 算法思想
时变型旅游行程设计问题的目标是在考虑到游客偏好和时变网络的情况下,在时间预算内确定旅游者的总效用最大化的最佳旅程,并通过移动设备向游客提供实时导航服务。在这个动态网络中,行程设计和行程时间取决于源节点的开始时间[19]。因此,从最佳时间开始产生最佳旅程以帮助游客在时间预算内访问其感兴趣的旅游点。本文提出了一种标签校正算法(LCA)[20]来解决动态旅游行程设计问题,该算法可以产生最佳旅行计划并在给定的时间预算内实现最大效用。
下面定义了算法中使用的一些符号:
定义1:Q是要处理的节点优先级队列,并满足先进先出(FIFO)原则。
定义2:Ci(t)是时刻t处源节点Vi的代价,代表时刻t从节点Vi到目的节点的旅行时间。
定义3:Uˉi(Vj,t)表示在时刻t到达节点Vi的总效用t(t∈ETij),其中Vi是后继节点(Vj∈S(i))。
鉴于开始时间是可变的,为了寻求最佳的开始时间和旅行路线,本文使用从目的地节点到源节点的标签校正算法。由于边缘旅行时间序列表示每个时间单位的边缘旅行时间,因此标签会记录每次从当前节点到目的地节点的旅行时间和总效用。该算法计算节点的出行效用和更新预节点的标签,重复上述迭代直到得到最优路径的最佳开始时间。
3.2 算法步骤
根据网络规划和动态规划的思想,本文提出了一种新的标签校正算法。
步骤1:初始化,给定每个边缘的两个属性:边缘时间序列ETij和旅行时间序列TTij。V1是源节点,Vn是目标节点。 pi表示旅游者对每个旅游点Vi的偏好值,停留时间为 vti,令 p1=pn=0,vt1=vtn=0。
步骤2:对于目标节点Vn,Cn(t)=0,=pn,t=1,…,T ,其中Vn+1是源节点Vn的虚拟后继节点,Q={Vn}。
步骤6:旅游路线的总效用最大化,根据最大效用的标签可以得到最佳的开始时间tbest。然后根据这个开始时间返回,将获得从源节点V1到目的节点Vn的最优路线,即 P(V1,Vn)={V1(tbest),V2(t2),…,Vn(tn)}。如果有多条路线的总效用最大,则选择最小C1(t)的路线作为最终的最优路线。
3.3 算法的时间复杂度分析
根据算法的步骤,可以看到当节点的旅行时间和标签是标量时,最坏情况下的时间复杂度为O(|V|2|E|)。由于每个标签是在时间序列长度为T时生成的,因此总计算时间为O(|V|2|E|T)。以上分析表明,本文的算法是一个多项式算法,可以满足实际应用。
步骤3:处理优先级队列Q中的节点:
1)对于Q中的Vj,从Q中删除Vj;
2)对 于 Vi∈P(j),计 算 Ci(t)=Cj(t+vtj+Tij(t))+Tij(t)+vtj,∀t∈ETij。 如 果 ci(t)>T ,则Tij(t)=∞,否则如果ci(t)≤T,则转到步骤3);
3)计算游客的总效用和标签,在时间t计算源节点Vi到目标节点的总效用。Uˉn(Vj,t)=Uˉj(Vk,t+vtj+Tij(t))+Pi,Vj∈S(i) ,Vk∈S(j) ,∀t∈ETij,标签为 (Vj,t,Ci(t),Uˉn(Vj,t));
4)节点Vi加入到Q中并进行更新;
步骤4:判断是否所有节点都已处理完成,如果Q≠φ,则转到步骤3,否则转到步骤5;
步骤5:计算路线的总效用,计算Uˉ(V1)=
4 数值仿真
该算法的效率和可行性将通过数值示例来仿真。假设给定一个如图2所示的游客游览图,其中V1是入口(源节点),V6是出口(目的节点),其他节点是访问点;每个节点的第一个数字表示停留时间,第二个数字表示游客的偏好值。旅行的时间预算是T=10,边上的数字是旅行时间序列。为了简化问题,边上的所有时间序列被设置为ETij=[1,2,…,T]。 ∀eij∈E ,如 果 t>T ,那 么Tij(t)=Tij(T)。本文将使用所提出的标签校正算法来解决上述例子,并且详细计算最优旅行。
给定在每条边eij上的时间序列ETij和旅行时间序列TTij,V1是源节点,Vn是目的节点。对于每个节点Vi,优先级值为 pi,停留时间为 vti,p1=pn=0,vt1=vtn=0。对于目的节点Vn,Cn(t)=0 ,Uˉn(vn+1,t)=pn,t=1,2,...,T ,假设Vn的后继节点为Vn+1(虚拟节点),Q={Vn}。优先级队列Q中的每个节点按照顺序处理,标签的轨迹如表1所示。

图2 时间相关的展览图
由表1可得每个节点的标签表示为三元数组{Sub,TS,TU},其中Sub表示子标签节点后继的索引,TS是标签节点到目的节点的旅行时间序列,TU是标签节点到目的节点的总效用,对于每个旅行时间系列,如果旅行时间在任何时间超过时间预算,则表示为“—”。
根据源节点V1的标签,最大总效用为Uˉn(V1)=17,最佳开始时间为tbest=3。在基于节点标签的路线获得最佳路线如下:

从上述算法的实现中可以明显看出,所提出的标签校正算法对于确定最佳开始时间是有效的,并且为提高游客满意度提供了最佳旅程方案。
5 结语
中国的城市旅游、商业展览、主题公园等各种观光展览活动发展迅速,对促进经济增长起到了重要作用。旅游行程设计问题不仅是旅行计划的重要内容,也是为游客提供优质服务的关键。随着移动通信技术的发展,移动导航能够根据地理位置为游客提供实时和个性化的服务。以往的研究忽视了展览网络中时变的特征。旅游交通网络是一个复杂的系统,具有很大的不确定性。展览网络中的旅游时间可能由于诸多因素而改变。因此,本文通过引入时间聚集图建立了基于时变网络的旅游出行设计模型,并提出了一种标签校正算法求解动态旅游行程设计问题,最后通过数值算例说明算法的有效性和可行性。下一步的研究将集中在多天的多次旅行设计问题上,这为旅客提供更满意和高质量的服务,同时将考虑到更多的现实因素,例如景点开放时间和容量限制。

表1 标签校正算法的标签追踪
