基于匹配圆的一种Smith圆图分区算法
2018-10-23孟恩林李丽华
孟恩林 刘 桐 李丽华
(海军工程大学电子工程学院 武汉 430033)
1 引言
短波通信是利用短波通过天波或地波传播的方式进行的通信,它具有设备体积小,隐蔽性好,战时抗毁能力强的特点,因此短波通信始终是军事指挥的重要手段之一。而天线调谐器是短波通信系统的重要组成部分,主要完成短波天线的输入阻抗与发射机输出阻抗之间的良好匹配,短波天线的输入阻抗随频率的变化而变化,而发射机功率级的输出阻抗是相对不变的[1~2],要想快速实现天线和发射机之间的阻抗匹配,天线的自动调谐就成为迫切需要解决的问题。
本文在参考文献[3]的基础上提出了针对Π型匹配网络在Smith圆图上的新分区调谐算法,并利用该算法对Π型网络元件的参数进行优化,达到了较好的调谐效果。
2 匹配网络
为使发射机的信号功率最大限度地通过天线辐射出去,天线的输入阻抗要与发射机的输出阻抗良好匹配。由于在短波频率范围内,天线阻抗随频率的变化比较大,而发射机功率级的输出阻抗是相对不变的,要想实现两者的阻抗匹配,需要在天线与发射机之间引入阻抗匹配网络。如图1所示,Z0为发射机输出阻抗,Za为天线输入阻抗,Zin为接入匹配网络后天线的输入阻抗。阻抗匹配网络通常采用电容电感等无耗元件来实现对天线的阻抗变换,从而减少功率损耗,提高辐射效率。
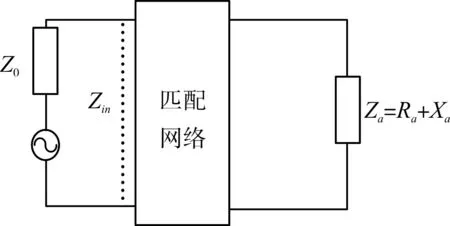
图1 天线阻抗匹配原理图
阻抗匹配网络通常采用电容电感等无耗元件来实现对天线的阻抗变换,从而减少功率损耗,提高辐射效率。常用的匹配网络有Γ型和反Γ型,Γ型网络用来匹配低于输入端阻抗的负载,反Γ型则用来匹配高于输入端阻抗的负载,两者都存在调谐盲区不能实现对所有天线的匹配,但将Γ型和反Γ型按不同方式级联构成的Τ型和Π型网络,理论上就能够实现对所有天线的匹配[3~7]。本文选用Π型网络作为调谐网络进行研究,如图2所示L1、C1、C2构成主调谐网络,为抵消杂散电感的影响,提高调谐效率,在电感L1后串联电容C3。

图2 Π型阻抗匹配网络简化结构
L1、C1、C2、C3是由一系列二进制离散值构成,调谐时通过控制继电器来改变接入网络的元件参数[8~14]。在设计射频电路时,经常利用Smith圆图代替复杂的计算来实现阻抗匹配[3]。Smith圆图是由很多阻抗圆和导纳圆交织在一起形成的一个圆,当并联电容C2时,A点沿着等电导圆顺时针移动到B点,再串联电感L1,B点会沿着等电阻圆顺时针移动到C点,最后并联电容C1,C点沿着等电导圆顺时针移动到D点,实现阻抗匹配。匹配网络的调谐过程如图3所示。
3 分区调谐算法
3.1 调谐分区
天线调谐器在实际应用中很难将天线阻抗精确调谐到Z0,一般要求驻波比达到一定程度时就认为已经匹配了[9]。本文中取驻波比VSWR≤1.2为阻抗匹配的条件,在Smith圆图中这一区域如图3所示是以Z0为圆心,VSWR=1.2为半径的圆内部区域,调谐时只需要将天线阻抗变换到该圆内即可。


图3 Π型网络的调谐原理

图4 匹配圆

根据以上分析和Π型网络的特点,将Smith圆图分为如图5所示的6个区域进行调谐。

图5 Smith圆图图分区
1区:Ga<G1,Ra<R1,Xa>0
2区:Ra>R1
3区:R2<Ra<R1,Xa<0
4区:Ra<R2,Xa<0
5区:Ga>G2
6区:G1<Ga<G2,Xa>0
3.2 调谐流程
天线调谐器开始调谐时,需要对天线阻抗进行实时精确检测,矢量检测技术能够满足分区调谐的要求。矢量检测获得Za的精确值后,匹配网络各元件的值是可以直接计算的,但由于L1、C1、C2、C3的值是离散的,只能参照计算值来接入调谐元件[10]。首先利用检测值判断天线阻抗所属区域,再按照不同的判断结果进入相应的分区调谐,具体流程如图6所示。

图6 调谐流程
1)1区调谐
1区调谐有两种方式,可以通过串联C3直接进入匹配圆或6区,也可以通过并联C2进入3区或4区调谐。计算天线阻抗相对于6区的电抗偏差ΔX:

2)2区调谐
计算将天线阻抗(Za=Ra+jXa)变换到3区的最小电纳值ΔB:

理论上应并入的最小C2为

若C2的组合值大于C2min,则将电容值大于C2min的电容依次并入,再进行阻抗检测确定所处分区;若不存在C2的组合值大于C2min,则说明无法将天线阻抗旋转到3区或4区,调谐失败。
3)3区调谐
3区调谐也有两种方式:直接串联L1将天线阻抗沿阻抗圆旋转到匹配圆内或并联C2将天线阻抗变换到4区进行调谐。
4)4区调谐
计算将天线阻抗(Za=Ra+jXa)变换到6区内的最小电抗值ΔX:
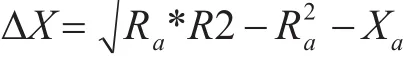
比较电感L1的最大值是否满足条件:ωL1max≥ΔX,若满足则串入相应的L1将天线阻抗沿阻抗圆旋转到6区;若不满足则并入C2,测量天线阻抗并重新计算ΔX,重复上述步骤,若最终仍不能将天线阻抗变换到6区,则调谐失败。
5)5区调谐
串入L1将天线阻抗沿阻抗圆旋转到6区,若串入L1最大值仍不能旋转到6区则调谐失败。
6)6区调谐
测量天线阻抗Za=Ra+jXa,计算天线阻抗到匹配圆的电纳偏差ΔB:

比较电容C1的最大值是否满足条件:ωC1max≥ΔB,若满足则并入相应的C1,将天线阻抗沿导纳圆旋转到匹配圆内;若不满足则调谐失败。
4 匹配网络参数
1)参数估算
匹配网络的参数对整个调谐过程起到关键的作用,因此需对网络参数进行估算。根据文献[15]介绍的Π型网络参数估算方法,本文以5m鞭天线作为调谐对象进行参数估算,结果如表1。

表1 匹配网络参数估算
2)参数优化
考虑到匹配网络的调谐性能主要与L1、C1有关,L1min和C1min的大小影响匹配轨迹圆进入匹配圆的“深度”[15],取值越小,匹配精度将越高,但在匹配范围不变的情况下会导致元件数量增加,电路控制难度加大;取值越大,匹配轨迹圆不能进入或超出匹配圆,降低调谐精度。因此,需对估算的网络参数进行仿真验证,确定匹配元件的最小值和元件个数。结合上文的分区调谐算法和网络参数估算,本文进行了Matlab仿真来优化网络参数。
(1)基于 C1min=10pF保持不变,L1min分别取0.02μH、0.03μH和0.04μH,仿真结果如图7所示,分析结果表明调谐后天线驻波比随着L1min减小而减小,在频率大于20MHz的频段改善效果明显。当频率f较小时,改变L1min对旋转轨迹移动步长(ΔXmin=ωL1min,ω=2πf)影响不大,但在高频段,改变L1min对旋转轨迹移动步长影响就很明显。当L1=0.02μH时,天线驻波比均低于1.2,调谐效果明显优于其它两个取值,但在中频段(5MHz~20MHz)调谐效果改善不明显。在低频段(3MHz~5MHz)出现调频失败,主要是改变了最小取值,元件个数不变,L1的取值范围减小不能实现对低频段天线的调谐,但可以通过增加L1的个数来改善天线驻波比。

图7 L1最小值对调谐结果的影响

图8 C1最小值对调谐结果的影响

表2 匹配网络优化后各元件参数
(2)L1min=0.02μH保持不变,C1min分别取10pF、15pF、20pF、30pF,仿真结果如图12所示。比较图中四条曲线,可以发现减小C1min对改善调谐驻波比效果并不明显。为了减少元件数量,降低硬件电路复杂度,取C1min=20pF,此时网络中电容C1的个数为9个。结合优化结果,最终确定匹配网络各元件参数如表2所示。
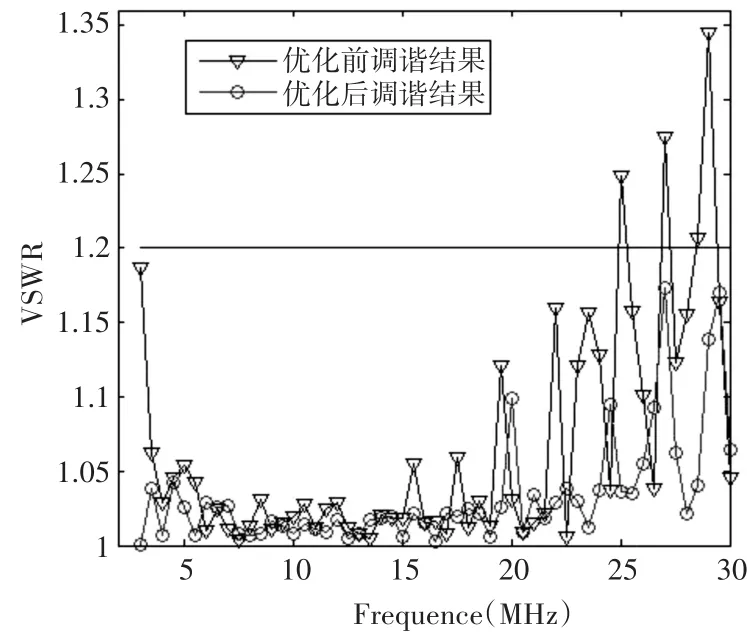
图9 参数优化调谐结果比较
由图9可知,在整个短波频段优化后的驻波比满足VSWR<1.2,明显优于优化前的匹配效果,整体的调谐匹配性能较好。
5 结语
本文在分析Π型匹配网络特点的基础上,提出了一种新的分区调谐算法,能准确地根据阻抗特性调整网络参数,调谐后天线驻波比为1.005~1.2,匹配性能好。通过对网络元件参数的估算和优化,为后续的电路设计及整体性能指标设计提供了参考。
