基于双图结构标签传递算法的高光谱数据分类
2018-10-23王小攀
王小攀 胡 艳
(重庆市地理信息中心 重庆 401121)
1 引言
高光谱遥感数据具有“图谱合一”的特性,能反映地物本质的物理化学特性[1]。利用高光谱遥感图像进行地物分类,可以判别地物的微小差别,常用于精细分类。高光谱遥感数据具有很高的维数,在样本点不足时会严重影响分类效果[2]。然而,高光谱遥感数据的类别标签信息需要经过实地考察和专家人工标注,需要耗费大量的人力、物力和时间代价[3]。
半监督分类算法利用少量标记数据和大量无标记数据构建分类模型,能够有效克服分类时样本点不足产生的问题。国际上对半监督分类算法已经开展了一定的研究,尤其是基于图的半监督分类算法是近年来研究的热点[4~5],并成功应用到高光谱遥感数据分类中[6~7]。常见的基于图的半监督分类算法包括最小分割(Mincut)[8],高斯随机场和调和函数(Gaussian Random and Harmonic Functions,GRHF)[9],局部和全局一致性(Local and Global Consistency,LGC)[10]算法,线性邻域传播(Linear Neighbor Propagation,LNP)[11]算法,基于非负稀疏表达的标签传递(Non-negative Sparse Representa⁃tion based Label Propagation,NSRLP)[12]算法等。这些算法的核心思想是构造一个图模型G(V,E),图中数据点作为顶点,数据的相似程度作为边权值。其中数据节点包含了少量有标记的数据和大量无标记的数据,边权值反映了数据点之间的相似程度,权值越大表示数据点间越相似,反之越不相似。基于图的半监督分类算法通常在图构造上应用某种策略,来实现对图结构的优化。
传统的图构造方法通常包括两个步骤:1)确定图的邻接结构;2)计算图上边的权重。K近邻(K Nearest Neighbor,K-NN)[13~15]是确定图的邻接结构中最常用的方法,其构造的K-NN图具有对称、稀疏等特性,很容易获得连通的图。Mincut、GRHF、LGC、LNP等基于图的半监督分类算法均采用K-NN策略选择图中的近邻点。采用K-NN确定图的近邻结构时,往往仅根据样本点相似性关系来寻找k个近邻点。然而,构造K-NN图对数据间的相似性度量算法异常敏感[16];NSRLP采用一种基于稀疏表达的近邻点选择方法,通过求解l1正则化最小平方问题得到稀疏系数向量[17],其中稀疏系数不为0,则表示数据点是近邻,稀疏系数图中边权值可以由稀疏系数表示。利用稀疏表达确定近邻点的方法能够有效避免相似性度量带来的不确定性,但是当样本点不足时,依然不能较好地保证近邻点具有同种类别,样本点近邻结构中一旦包含了来自其他类的邻居类别的数据点,很容易造成标签的错误传递甚至累积扩大。
为了有效地解决上述问题,提高图结构对高光谱数据内在几何流形描述的准确性,本文提出一种基于属类概率的方法来确定图的邻接关系。将属类概率图与K-NN图通过拉普拉斯矩阵线性组合起来,构成双图结构。双图结构具有K-NN图和属类概率图共有的特性和优点,能更准确地获取样本点间的邻接结构,提高图的性能。将本文提出的双图结构嵌于标签传递算法框架中,得到一种基于双图结构的标签传递算法(Couple Graph based Label Propagation,CGLP)。将CGLP算法应用于高光谱遥感图像分类中,实验结果表明在标签传递算法框架下,组合图的构图效果要明显优于K-NN图和稀疏系数图,有效提高了高光谱遥感图像分类精度。
2 图的构造
2.1 K-NN图
构造K-NN图的主要步骤包括:1)根据数据点间的灰度相关性,采用k近邻策略确定图的邻接关系。当数据点xi是xj的k近邻,或者xj是xi的k近邻时,这两个点被认为是邻居,其中k为正整数;2)计算近邻点间的边权值Wij,常用的边权值计算方法包括二值函数,高斯核函数等。其中高斯核函数计算边权值方法如下:
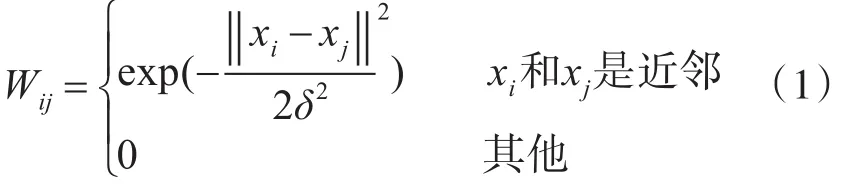
其中,‖‖表示样本点xi是xj的距离,K-NN图的邻接关系对距离度量方法较敏感。δ为尺度参数,当δ→∞时,热核函数权重就变成为二值权重,且如果xi和xj是近邻,Wij=1,否则Wij=0。相似图权值的矩阵形式记为:(W)i,j=Wi,j;令 L=D-W,其中 L表示相似图拉普拉斯矩阵,D是相似图权值矩阵W的对角元素之和
2.2 属类概率图
构造属类概率图主要步骤包括:1)计算属类概率,确定图的邻接关系;2)高斯核函数计算图的边权值,构造属类概率图。其中属类概率通过求解l1正则化最小平方问题得到。构造属类概率图的基本步骤如下:
Step1稀疏向量求解。假设数据有C个类别,C={1,…,c},令 A=[A1,A2,…,Ac]代表原始的训练样本集,其中Ai∈A表示训练样本集中属于第i类的子样本集。YL∈Rl×c表示数据的真实标签信息,当数据点 xj的标签 Yj=i,i∈ C 时,(YL)j,i=1,否则(YL)j,i=0。X0表示测试数据,通过求解最小化l1范数问题,对X0在训练样本集A上进行稀疏编码,得到稀疏向量 αˆ:
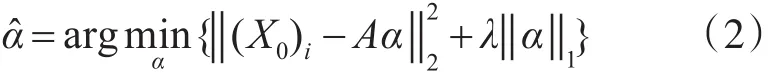
其中,λ是尺度参数,α为测试样本在训练集A上的投射系数向量,得到的解αˆ是一个稀疏向量,即只有少数元素不为零。此时,测试数据X0可完全或近似地由非常少的一组样本的线性组合表示。
Step2利用稀疏向量计算属类概率。令P((X0)i)=[P((X0)1,i),…,P((X0)c,i)]T∈ R1×c表示测试数据点(X0)i属于每个类别的概率向量。其中,P((X0)c,i)表示数据点(X0)i属于类别c的概率,c∈C。我们可以得到数据点(X0)i属于每个类别的属类概率向量:

对数据属于每个类别的概率信息进行归一化处理,归一化后的属类概率表示为
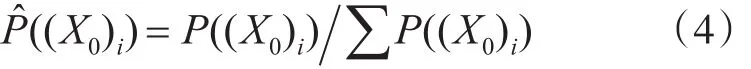
令P(xi,xj)表示数据点xi和xj属于同一类别的概率。假设xi和xj是两个独立的样本点,且不能同时具有标签信息。xi和xj属于同类的概率P(xi,xj)可以通过以下概率公式计算:
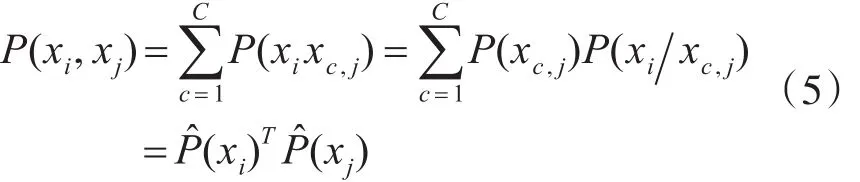
Pˆ(xi)和 Pˆ(xj)可由式(3)计算得到。此外,当数据点xi和xj具有相同的标签时P(xi,xj)=1,反之,xi和xj具有不同的标签时P(xi,xj)=0。因此,属于同类的概率可以表示为如式(6)所示:

P(xi,xj)是描述数据间相似关系的概率矩阵。P(xi,xj)越大表示数据点xi和xj越相似。
Step3计算邻接点的边权值,构造属类概率图。传统的图构造方法采用“k-NN”策略来选择近邻点,我们采用这个代表数据相似性的概率矩阵来选择近邻点。设定一个阈值T(0<T<1),当xi和xj的相似概率小于等于阈值T时P(xi,xj)≤T,表示xi和 xj两点不是近邻,且 Si,j=0,当 xi和 xj的相似概率大于阈值T时P(xi,xj)>T,表示xi和xj两点是近邻,且Si,j=1。属类概率图权值矩阵W˜可以由热核函数(Heat Kernel)计算得到。
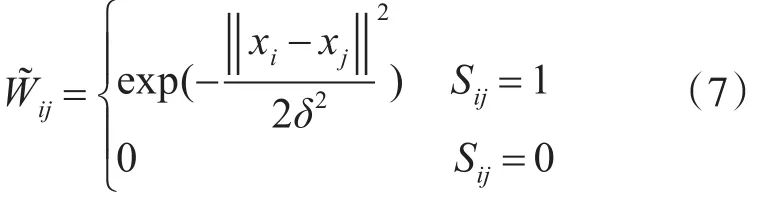
由于W˜是非对称矩阵,按照非对称矩阵的拉普拉斯计算方法[18],表示稀疏图的行拉普拉斯矩阵,表示稀疏图权值矩阵W˜的行和表示稀疏图的列拉普拉斯矩阵,表示稀疏图权值矩阵W˜ 的列和。表示稀疏图的拉普拉斯矩阵。
3 基于双图结构的标签传递算法
将K-NN图与属类概率图嵌入标签传递算法框架中,获得一种基于双图结构的标签传递算法。GCLP算法能够更好地描述数据结构,使得算法能够更好地利用数据的相似性进行分类。GCLP算法需要最小化目标函数:
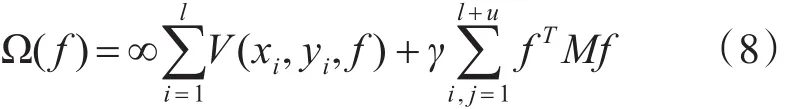
其中γ是一个调整参数,第一项是损失函数。第二项是平滑项。M表示混合的图拉普拉斯矩阵,由k-NN图拉普拉斯矩阵L和稀疏图拉普拉斯矩阵L˜线性组合表示:
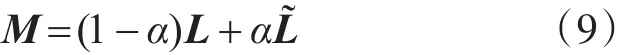
其中α是调整参数。混合图拉普拉斯矩阵M反映了数据组合的图结构。平滑项可展开为
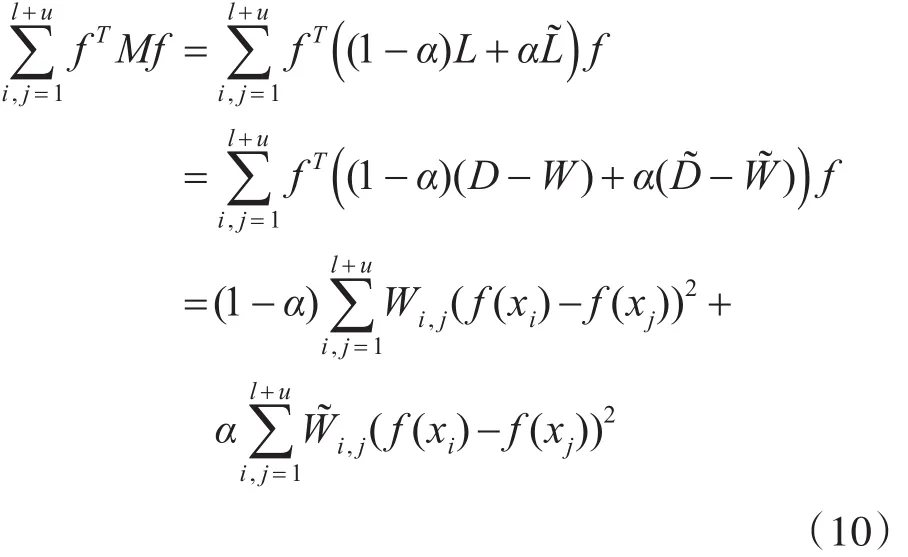
其中α是K-NN图和属类概率图间的调整参数,f代表数据集的预测结果。
下面我们来求解其收敛式。令 f=[f1,…,fl,…,fN]T∈RN×c代表数据集…,xN}的一种分类结果,样本点xi的标记为。 定 义 Y=[Y1,…,Yl,…,YN]T∈RN×c为数据集 X的初始标记矩阵,如果xi的标记为yi=j,则 Yi,j=1,否则 Yi,j=0,j∈ C;将无标记样本的Yi,j设置为0。将 f和Y转化成分块矩阵其中fL和YL分别是标记样本的预测标签矩阵和标签矩阵,fU和YU分别是未标记样本的预测标签矩阵和标签矩阵。标记传播算法不允许改变标记样本的真实标记,因此限制fL=YL。将混合图拉普拉斯矩阵 M从l行,l列分成四个小矩阵块设置γ=1/2,并在式(8)左右两边对f求导,即Δf=0。算法预测无标签数据收敛式可表示为
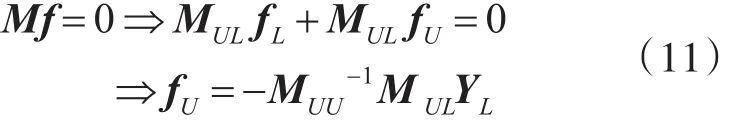

表1 CGLP算法描述
4 高光谱遥感数据实验结果与分析
4.1 数据描述
为了验证本文算法对高光谱数据分类的有效性,实验两组高光谱遥感数据:第一组采用了EO-1卫星搭载的Hyperion高光谱遥感数据,于2001年5月在Okavango Delta,Botswana(BOT)地区采集,其空间分辨率为30 m×30 m,光谱分辨率10 nm,具有242波段的去除未校准波段、噪声波段以及光谱重叠波段,剩余145个波段。实验中,采用BOT数据全部9个类别(C1~9)数据进行分类实验;第二组实验数据是1996年3月在美国肯尼迪航天中心(KSC)拍摄的高光谱图像,具有个224波段,光谱范围是400nm~2500nm,光谱分辨率10nm,空间分辨率18m×18m。KSC数据的13个标记类别分别采样于湿地和高地区域,存在较严重的光谱混合。实验数据所包含的地物类别如表2所示,其中,类别名称下括号中的数据表示该类别实验数据的个数。
4.2 参数分析
本文算法共有5个自由参数,分别是调整参数α(0<α<1),相似图中近邻点的个数k以及热核函数的尺度参数δ1,不相似图中热核函数的尺度参数δ2以及阈值T(0<T<1)。k取值范围从10到50每隔5采样一次;δ1和δ2的取值范围是{0.001,0.01,0.1,1,10};α的取值从0.1~0.9,每间隔0.1采样一次;阈值T的取值范围从0~0.9,每隔0.1采样一次。本实验采用穷举法,遍历每个可取参数,取最优参数作为实验结果。为提高实验的可靠性并对本文算法的分类效果进行有效评估,对3组高光谱遥感图像数据集进行了重复实验,随机产生10次有标记数据和未标记数据的划分,并取这10次划分上的平均分类率作为最终的结果。每次实验,我们分别从每类样本中随机选取3、5、10、20、30的样本点作为训练样本点,其余的作为测试样本集。在高光谱数据实验中,选择光谱信息散度作为样本点间的距离度量算法,能够较好地适应高光谱数据的高维特性。
4.3 实验结果分析
实验将本文算法CGLP与GRHF、LNP、NSRLP算法对高光谱数据的分类精度进行了对比分析。其中GRHF、LNP和NSRLP算法均为标签传递算法框架下的半监督分类算法,但图构造方法不同。非负稀疏表达(Non-negative Sparse Representation Classification,NSRC)[19]算法是一种有监督的分类算法,与NSRLP、CGLP算法类似,都通过求解l1正则化最小平方问题得到稀疏系数向量,NSRC算法将稀疏系数最大的类作为测试数据的标签。因此,我们还将NSRC算法与本文算法进行对比。CGLP算法与GRHF算法构造K-NN图的方法是一致的,当调整参数α=0时本文算法CGLP等价于GRHF算法。
图1、图2分别展示了是BOT数据C1-9全类和KSC数据C1-13全类的分类结果比较,图中记录了本文算法与GRHF、LNP、NSRC、NSRLP算法十次实验的平均分类精度和分类误差,以及在不同训练样本数情况下的分类结果变化趋势。表3、表4分别给出了上述5种算法在不同训练样本数时,BOT数据C1-9全类、KSC数据C1-13全类的总体分类精度(Overall Accuracy,OA)以及Kappa系数比较(十次实验结果的平均值)。结合图1、图2、表3、表4可以得到几点结论:

图1 BOT数据C1-9全类在不同训练样本数时平均分类精度与分类误差比较
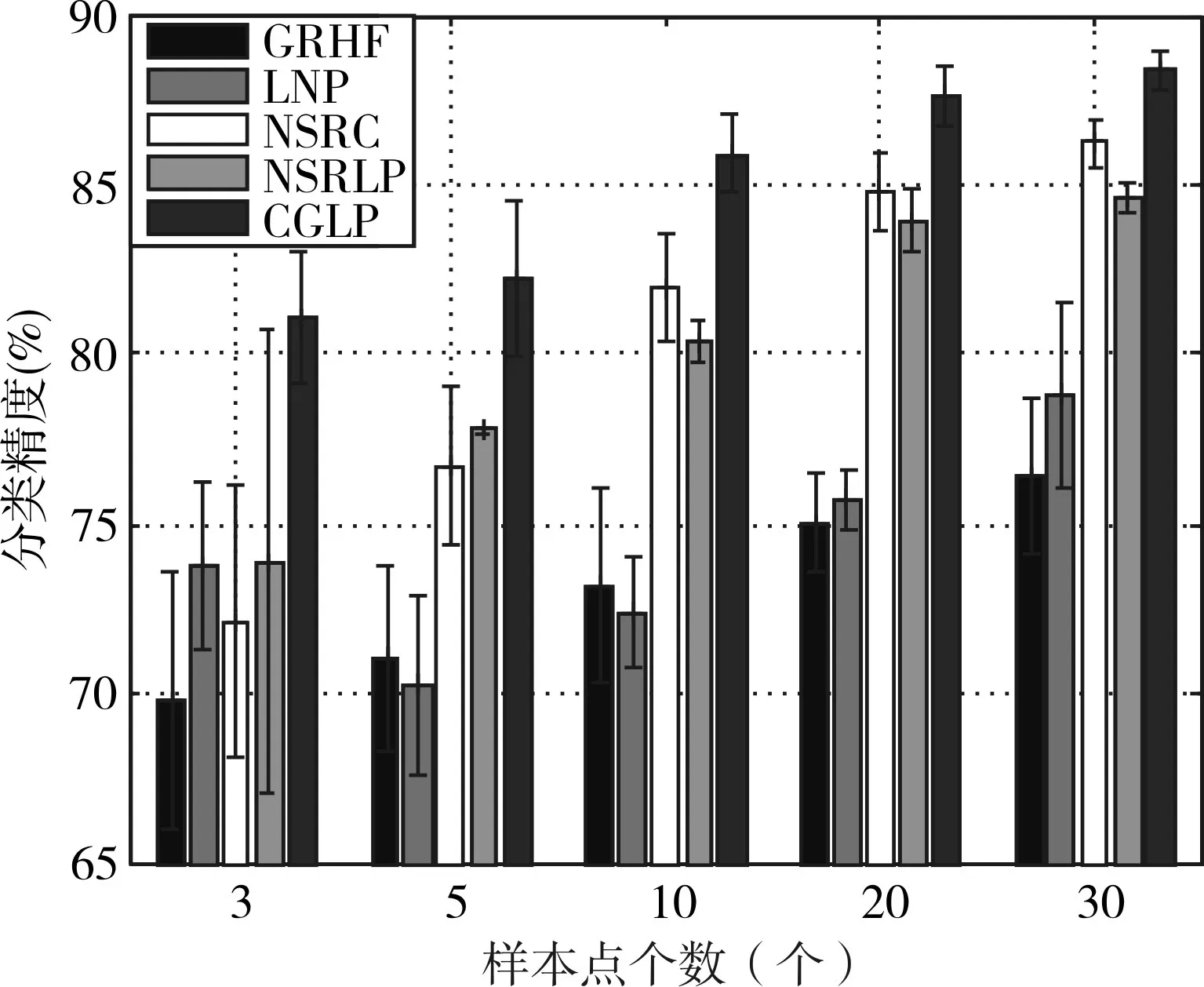
图2 KSC数据C1-13全类不同训练样本数时平均分类精度与分类误差比较
1)对BOT数据C1-9全类和KSC数据C1-13全类的分类结果来看,CGLP算法的分类精度均明显优于GRHF算法,表明采用K-NN图结合属类概率图的双图结构能够更好地挖掘高光谱数据的特性,对分类效果有明显提高;
2)在选择不同训练样本数量的情况下,CGLP算法对BOT数据C1-9全类和KSC数据C1-13全类的总体分类精度和Kappa系数均明显优于其他四种分类算法;
3)对于BOT数据C1-9全类,随着训练样本数的增加,CGLP算法分类精度优于其他四种算法程度越明显。当每类训练样本数为3时,CGLP较算法分类精度次优的GRHF算法,分类精度提高不到1%,随着训练样本点数量的增加,当每类训练样本数达到30时,CGLP算法较分类精度次优的NSRC算法,分类精度提高接近2%;
4)对于KSC数据C1-13全类结果,训练样本数越少,CGLP算法分类精度优于其他四种算法程度越明显。当每类训练样本数为3时,CGLP算法较分类精度次优的NSRLP算法,分类精度提高超过7%,随着训练样本点数量的增加,当每类训练样本数达到30时,CGLP算法较分类精度次优的NSRC算法,分类精度提高不到4%;
5)NSRC算法作为一种有监督的分类算法,在样本点少的时候分类精度不好,但随着训练样本数增加,分类精度有很大提高,甚至优于NSRLP、GRHF、LNP等半监督的分类算法,也验证了半监督的分类算法更适用于样本点较少的情况。
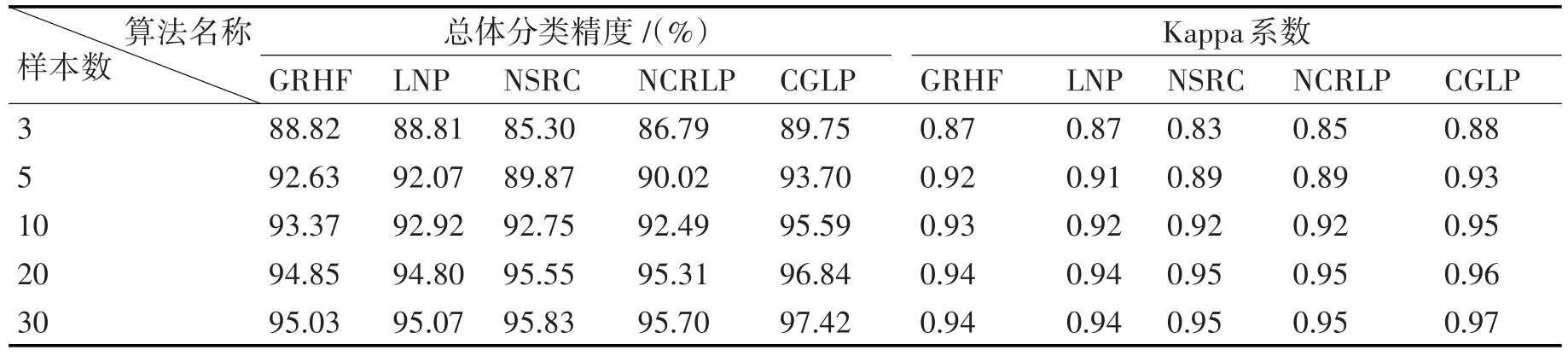
表3 BOT数据5种算法在不同训练样本数时总体分类精度和Kappa系数的比较

表4 KSC数据5种算法在不同训练样本数时总体分类精度和Kappa系数的比较
5 结语
本文提出了一种基于属类概率选择近邻结构的图构造方法,与基于稀疏表达确定近邻点的图构造方法相比,能够在样本点不足的情况下依然在同一流形中保持相同的类别,进而减少标签传递过程中错误的累积甚至扩大。为了更好地挖掘数据间的内在联系,本文将这种属类概率图与K-NN图组合起来,并嵌入到标签传递算法框架中,得到一种双图结构的标签传递算法。将CGLP算法应用到两种高光谱数据上,分类结果表明CGLP算法能有效提高高光谱数据的分类精度。本文的研究工作还存在很多有待改进的地方,例如双图的组合方法上不仅局限于线性的方法,还可以采取其他的组合方法;此外基于多图结构的半监督分类算法也是下一步研究的方向。
