多无人机协同任务分群方案研究
2018-10-23谢瑞煜杨利斌赵建军
王 毅 谢瑞煜 杨利斌 赵建军
(海军航空大学 烟台 264001)
1 引言
多UAV联合起来协同完成搜索、侦察、监视、打击等作战任务,已经在军事上有初步应用,显示出十分良好的应用前景,受到越来越多研究者的关注。多UAV对海及对地协同侦察是很有代表性的问题。侦察问题中,由多UAV同时对给定区域的多个任务点进行侦察,由于侦察任务较多,需要事先进行任务分群和任务分配,任务分群不仅可以较清楚地反映战场态势,而且可以减少系统的计算量。使UAV之间相互协作,依据具体的指标要求提高整体的侦察效率[1]。
2 多UAV协同侦察任务分群
2.1 侦察任务分群建模
多UAV侦察任务分群问题的数学语言描述为,将任务集合T={T1,T2,…,TM}按一定原则划分为一系列任务簇A={A1,A2,…,AS},Ai中成员为{Ti1,Ti2,…,Timax} ,i=1,2,…,S ,【2】满足:
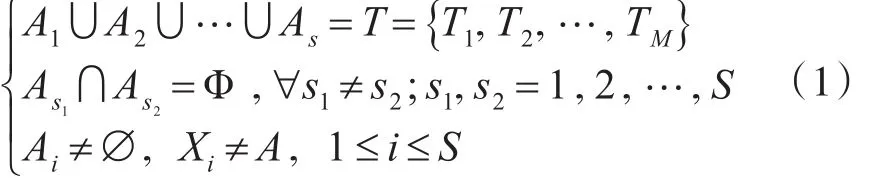
将UAV集合V={V1,V2,…,VN}划分为不同编队F={F1,F2,…,Fk},满足:
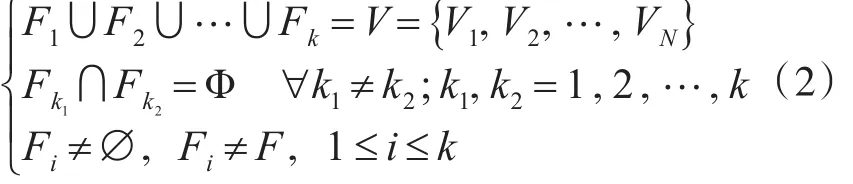
定义“编队-任务簇”分配矩阵:

2.2 任务分群性能优化指标分析
2.2.1 任务群分布指标

2.2.2 任务数量均衡指标
定义任务数量均衡率:
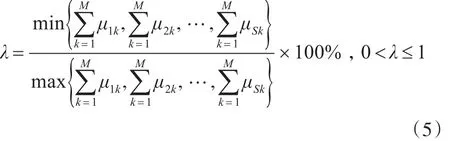
2.2.3 巡航时间均衡指标
要达到比较均衡,应使每架飞机的巡航时间基本相同,根据分类算法得到的子图分别运用禁忌搜索算法求得其最短侦察路径ψi,i=1,2,…,S和最短侦察时间 t(ψi),i=1,2,…,S[4]。
定义任务执行时间均衡率:

若η接近于1,则上面划分的任务就可以接受。否则的话,根据t(ψi),i=1,2,…,S的大小用局部搜索算法调整,从而调整各分区内点的个数,直至任务达到均衡。
2.2.4 总体优化函数建模
针对任务分群性能优化指标[5~7],得到任务分群的总优化函数值计算方式:

2.3 K均值动态聚类任务分群算法
聚类分析就是按照一定的规律和要求对事物进行区分和分类的过程,在这一过程中没有任何关于分类的先验知识,没有教师指导,仅靠事物间的相似性作为类属划分的准则。聚类属于无监督机器学习的范畴。K均值算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。若不正确,就要调整,在全部样本调整完后,再修改聚类中心,进入下一次迭代。如果在一次迭代算法中所有的样本被正确分类,则不会有调整,聚类中心不会再有变化[8]。
K均值算法能够使得聚类域中所有样品到聚类中心距离的平方和最小,其原理为算法首先随机从数据集中选取k个点作为初始聚类中心,然后计算各个样本到这k个聚类中心的距离,把样本归到离它最近的那个聚类中心所在的类。计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心,直到新的聚类中心与上一次的中心没有任何变化,则样本调整结束[9]。数学模型描述如下:
假设任务集合T={T1,T2,…,TM},按一定原则划分为一系列任务簇A={A1,A2,…,AS},且满足:

K均值动态聚类法实现步骤如下:
Step1:选择k个初始凝聚点,作为类中心的估计;
Step2:对每一个样本,按照最短距离原则划归某个类中;
Step3:重新计算各类的重心;
Step4:跳转到Step2直到各类重心稳定。
2.4 K均值聚类算法优化
基本的K均值算法目的是找到使目标函数值最小的K个划分,算法思想简单,易实现,而且收敛速度较快。如果各个簇之间区分明显,且数据分布稠密,则该算法比较有效,但如果各个簇的形状和大小差别不大,则可能出现较大的簇分割现象,此外,在K均值算法聚类时,最佳聚类结果通常对应于目标函数的极值点,由于目标函数可能存在很多的局部极小值点,这就会导致算法在局部极小值点收敛,因此初始聚类中心的随机选取可能会使解陷入局部最优解,难以获得全局最优解[10]。
基于模拟退火思想对K均值聚类算法进行优化,模拟退火算法是一种启发式随机搜索算法,具有并行性和渐近收敛性。理论上证明它以概率1收敛于全局最优,因此,用模拟退火算法对K均值聚类算法进行优化,可以改进K均值聚类算法的局限性,提高算法性能。基于模拟退火思想,将内能E模拟为目标函数值,将基本K均值聚类算法的聚类结果作为初始解,初始目标函数值作为初始温度T0,对当前解重复“产生新解→计算目标函数差→接受或舍弃新解”的迭代过程,并逐步降低温度,算法终止时当前解为近似最优解,该算法开始时以较快的速度找到相对较优的区域,然后进行更精确的搜索,最终找到全局最优解[11~12]。
2.5 基于模拟退火思想的改进K均值聚类算法
算法实现步骤如下:
Step1:对样本进行K均值聚类,将聚类划分结果作为初始解A,根据当前聚类划分的总类间离散度指标,计算目标函数值;
Step2:初始化温度T0,令T0=JA。初始化退火速度a和最大退火次数;
Step3:对于某一温度t,随机扰动产生新的聚类划分A',即随机改变一个聚类样品的当前所属类别,计算新的目标函数值JA';
Step4:算新的目标函数值与当前目标函数值的差ΔJ=JA'
-JA,判断ΔJ是否小于0;Step5:若ΔJ<0,则接受新解,保存聚类划分A'为最优聚类划分,JA'为最优目标函数值,将新解作为当前解;
Step6:若 ΔJ≥0,根据Metropolis准则,以概率p=eΔJ/Kt接受新解,K为常数;
Step7:判断是否达到最大退火次数,是则结束算法,输出最优聚类划分,否则根据退火公式对温程序设计流程图如图1所示。
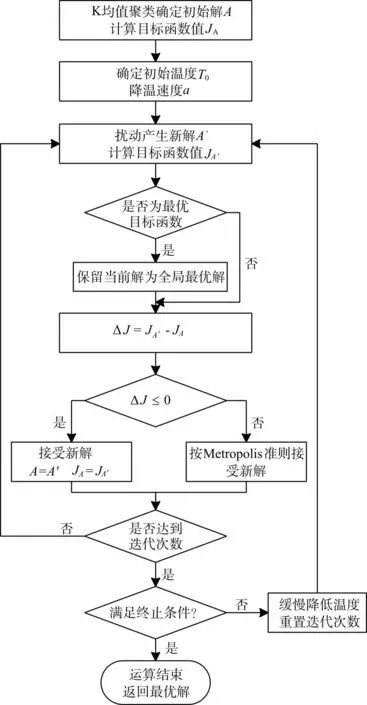
图1 基于模拟退火思想的改进K均值聚类算法流程
3 仿真分析
假设敌方100个任务点的GPS经纬度坐标如表1所示。
100个任务从左到右按列排序,由于给定的是地理坐标(经度和纬度),我们必须求两点间的实际距离。设A,B两点的地理坐标分别为(x1,y1),(x2,y2),过A,B两点的大圆的劣弧长即为两点的实际距离。以地心为坐标原点O,以赤道平面为XOY平面,以0°经线圈所在的平面为XOZ平面建立三维直角坐标系。如图2所示。

表1 100个任务点的GPS经纬度坐标

图2 GPS经纬度坐标转三维直角坐标示意图
则A,B两点的直角坐标分别为
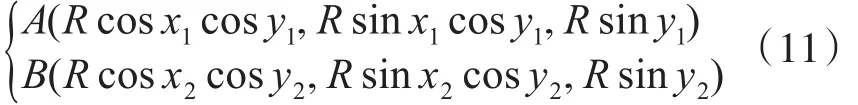
其中地球半径R=6370km。
A,B两点的实际距离:

我方有三个基地,经度和纬度分别为(10,60),(30,60),(50,60)。假设我方所有无人侦察机的速度都为1000 km/h。三个基地各派出一架飞机侦察敌方任务
首先用K均值聚类法通过聚类分析得到初始分群结果,再采用基于模拟退火思想的改进K均值聚类法得到优化分群结果,如表2所示。
规划出无威胁情况下算法改进前后的最短航路,为了显示的直观方便,选用经纬度坐标。
这样划分任务方案,使得巡航时间最短,目标群分布群内比较集中,群间比较分散,且各UAV任务分配比较均衡。

表2 算法改进前后最优任务分群方案表
其中,1代表该任务分配给UAV1,在图中以○表示;2代表该任务分配给UAV2,在图中以△表示;3代表该任务分配给UAV3,在图中以☆表示;()内代表优化后的分群方案。

图3 算法改进前后任务分群与任务规划方案
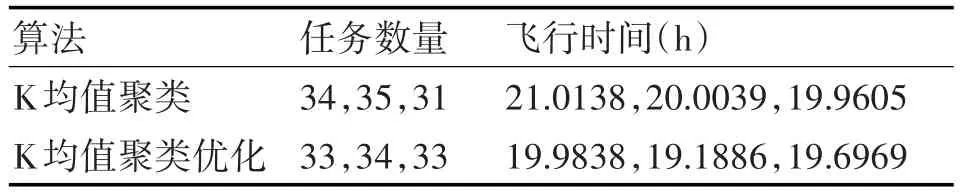
表3 任务分群与各无人机巡航时间表
4 结语
文中针对多UAV协同侦察任务分群问题,建立了侦察任务分群模型,提出了评价任务分群性能好坏的3个优化指标,这些指标代表群内聚集,群间分散,以及任务数量均衡和巡航时间均衡等性能。采用基于模拟退火思想的改进K均值聚类算法进行任务分群和寻找最短路径。仿真结果表明,基于模拟退火思想的改进K均值聚类算法能够有效解决任务分群问题,符合部队的实际情况。
