连续相位调制通信系统性能分析及仿真实现

刘翠海 魏 冉 周航程

（1.海军潜艇学院航海观通系 青岛 266199）（2.海军潜艇学院研究生队 青岛 266199）（3.中国人民解放军91033部队 青岛 266199）

1 引言

在现代通信中，随着资源的日益紧张和数字通信技术在各个领域的广泛应用，如何在带宽资源有限以及信道非线性条件下更快、更可靠地传输数据信息，成为迫切需要解决的热门问题。

连续相位调制（Continuous Phase Modulation，CPM）信号是一类恒包络、相位变化连续调制信号的总称，具有较高的频谱利用率和功率利用率，是由最初的相移键控（PSK）调制技术发展而来，根据内部状态和输入符号向信道发送相位连续的恒包络波形，在具体应用时，可以有多种形式。由于包络恒定，它对功放的非线性特性不敏感；而相位连续的特性，使得其带外辐射小，从而产生较小的邻道干扰。与其他调制信号相比，其优越的性能使得其特别使用于移动通信、卫星通信、军用短波电台及战术数据链当中。

2 CPM调制原理

2.1 CPM信号表达式

CPM信号通常定义为

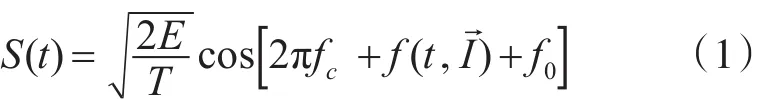
式（1）中E为信号码元能量，T为码元周期，fc为载波频率，f0为初始相位，代表时变调制信号信息的时变相位函数。表达式为

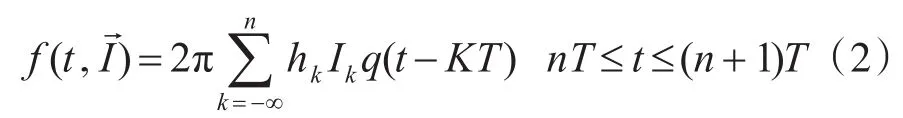
式（2）中 I={Ik}，k为整数，Ik表示M进制（常取M=2p，P为 1，2…）符号，取值为｛±1，±3，…±（M-1）｝；调制指数h常定义为h=m/p，m与h互素且为整数；T为码元周期，q(t)为响应函数，它是脉冲函数g（t）的积分，即：。式（2）的含义为CPM的相位由从0时刻开始的所有符号的某种累加构成，每个符合对相位的贡献在q()t控制下从零逐渐增大，直至几个符号周期后保持恒定，调制指数h控制相位变化的快慢程度。

虽然脉冲函数g（t）是不连续的，但对它的积分q（t）却是连续的，因此q（t）的连续性也决定了调制信号相位 f(t,的连续性。g（t）在区间t∈（0，LT）内为非零值。根据L取值范围不同，有下列情形：

1）当 L=1 时，即t＞T 时，g（t）=0，称为全响应CPM信号；

2）当L＞1时，即t＞T时，g（t）≠0，称为部分响应CPM信号。

这里L称为部分响应长度或关联长度。

2.2 调制状态

CPM信号的频率脉冲响应函数g（t）是表征的重要参量，与信号质量息息相关。根据g（t）的不同，会有不同的CPM定义，常见的脉冲函数g（t）有两种较常用的脉冲形状：矩形脉冲REC和升余弦脉冲RC，它们的表达式分别为

故式（2）可以表示为

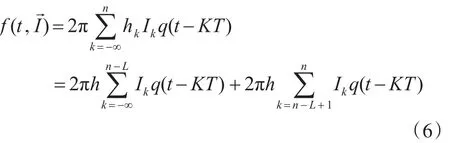
对于调制指数h的CPM信号，在nT≤t≤（n+1）T时间段内即第n个码元间隔内，当k≤（n-1）时，有t-kT≥LT。此时，式（5）中表示为

2.2.1 相位状态

相位状态θn是一个迭代累加值，它的轨迹可在t=nt时刻确定相位终值，在这种情况下，限制调制指数h为有理数，定义h=m/p（m、p为互素整数），θn经过模2π计算得到全响应CPM信号终值相位状态：

1）当m为偶数时：

2）当m为奇数时：

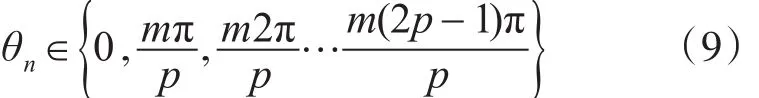
当m为偶数时，有p个累计相位；而当k为奇数时，有2p个累计相位。

2.2.2 关联状态

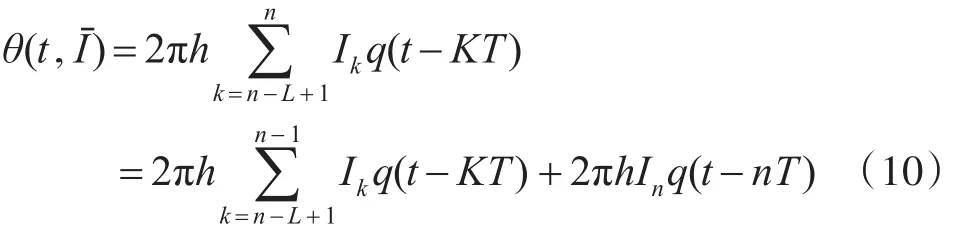
上式中，等式右边第一项由信息符号(In-1,In-2,…,In-L+1)决定，称为相关状态向量，此项表示相应于最终值的信号脉冲的相位项。式中2πhInq(t-nT)表示最近的符号In的相位贡献，只与当前时刻的输入符号In有关。因此，t=nt时刻，CPM信号的相位状态由关联相位及累计相位θn共同决定，记为

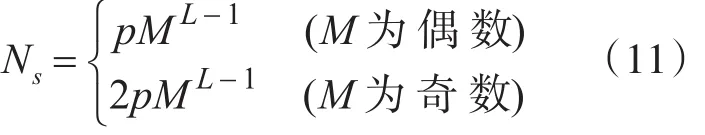
上式中，p为相位个数，L为关联长度。

对CPM调制信号波形表达式，进行变换，并将相 位 状 态

上式中，fc为载波频率，f(t,+f0是载波相位，f0是初始相位，Ik是M进制的输入信号符号，Ik取值范围为Ik∈{± 1,±3,…±(M-1)} ，h为调制指数，h=m/p，T为码元间隔宽度，q(t)是响应函数。

3 参数选择对CPM信号的影响

3.1 调制参数h对CPM信号的影响

在分析调制系数h对功率谱密度影响之前，需要先确定其它的调制参数，本文选取M=2、L=3，调制脉冲为RC的CPM信号，以载波频率为100HZ的单指数CPM信号为例，采用M=2、L=3，频率脉冲为REC，四个不同的调制指数分别是1/16、4/16、5/16、9/16，结果如图1所示。

从方针结果来看，不同调制指数的CPM信号均满足恒包络特性。但仅从图观察，指数越小，其波形类似频率变化的特征越不明显，则CPM信号质量越好，越不容易被识别出来，反之，越明显。

图1 调制参数h对CPM信号的影响

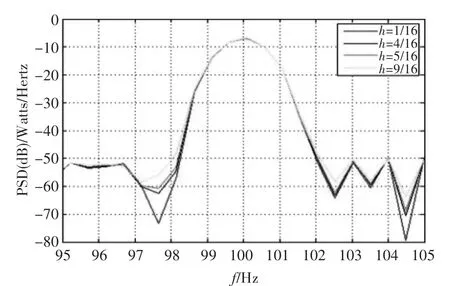
图2 CPM调制信号s（t）的功率谱密度

如上图所示，四个不同单指数CPM的频谱，可见，功率谱均较集中，指数越小，占用频带越窄，信号能量越集中，过渡带也越窄，越利于信号在更窄的信道上传输；指数越大，与其相反。但是，指数越小，相位变化越不明显，会增大解调判决的复杂度。综合考虑，单指数时，一般选择

3.2 关联长度L对CPM信号的影响

关联长度L是CPM信号的重要参数之一，它与累计相位和关联相位密切相关。仅从原理上分析，L越大，单位符号持续时间内包含信息也越多。总相位状态数NS=PML-1与L呈指数相关。L变长，导致计算复杂度呈现指数增加，且L越长会致使相关脉冲之间的差别越小。因而，L变长，解调难度越大，误码率也越高。

从上图可知，L越长，其信号频谱的频带越窄，信号能量越集中。

3.3 进制M对CPM信号的影响

进制M直接影响每个符号持续时间内所携带的信息量。M越大，单位符号持续时间内所携带的信息量越多，但解调判决时分析更困难，解调也更复杂。从前面提及的相位状态Sn可知，其相位总数NS=PML-1，是以M为基的指数关系，也印证了随着M增大，其解调的计算复杂度急剧增加。因此，在工程实践中，采用M=2的情景最普遍，如采用GMSK和GSM系统，其次，在一些特殊的场景下，会采用M=4 或 8。再高阶时，解调的计算复杂度和时延都难以接受。

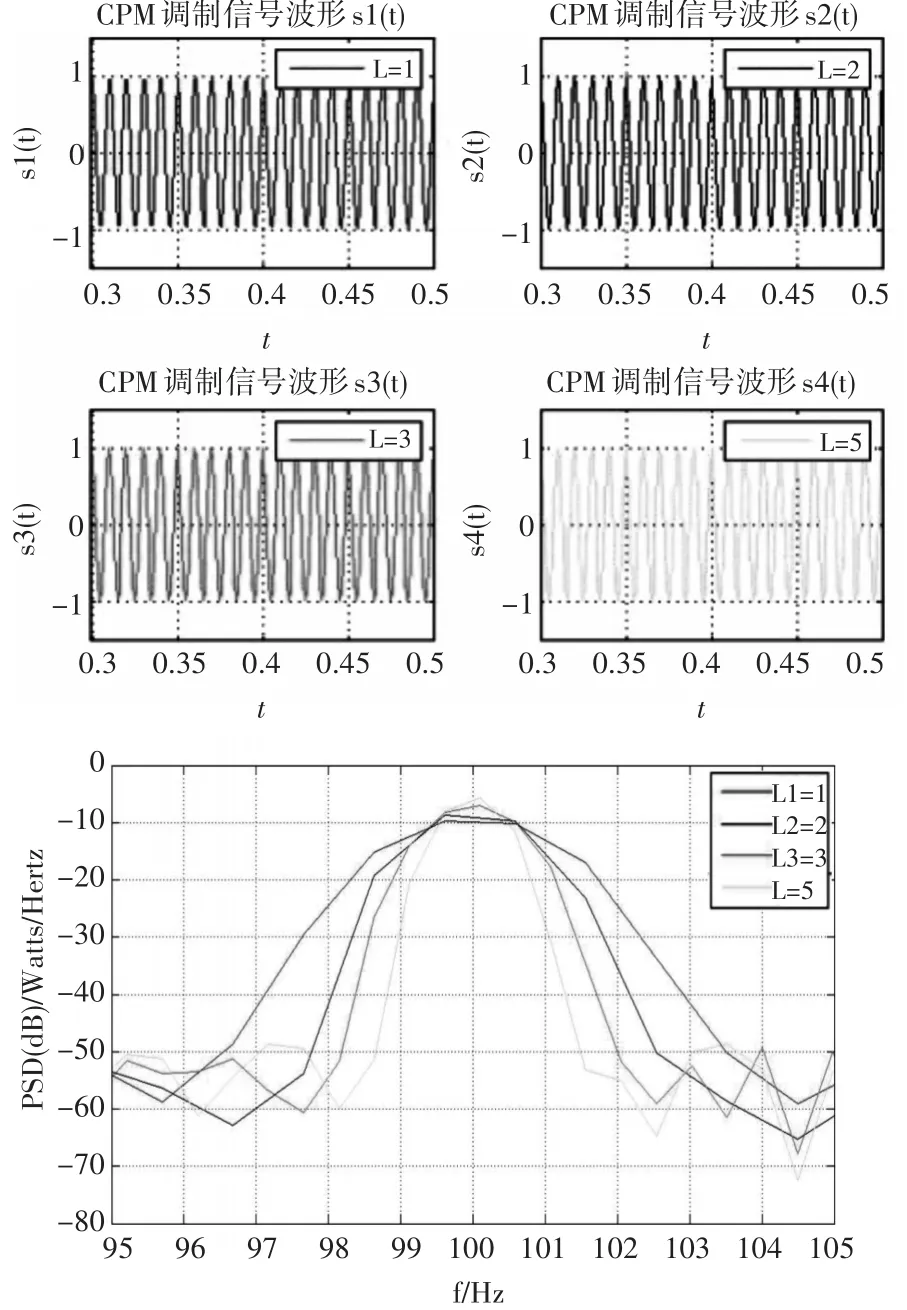
图3 关联长度L对CPM信号的影响

3.4 频率脉冲响应选择对CPM信号的影响

频率脉冲是影响CPM的性能参数之一。由仿真结果，选择不同频率脉冲对CPM信号的频谱影响不大。但是采用矩形脉冲且关联长度L为偶数时，在部分符号持续时间内，关联数据映射后是符号相反的序列，则该符号持续期间实际相位为某一恒定值，这对整体解调影响不大。若信息序列映射后都是符号相反交替出现时，就会导致实际相位为恒定值。一旦未同步或者同步错误，就会导致解调完全错误。因而，在关联长度L为偶数时，应避免选择矩形脉冲。而多指数则不存在这种困扰。此外，解调信息时，频率脉冲会影响解调匹配度，尤其在噪声信道下，频率脉冲越复杂，误码性能越好，最常用的是升余弦脉冲。

图4 频率脉冲响应选择对CPM信号的影响

4 结语

从以上的仿真结果与实际应用情况看，在多进制CPM调制技术中，CPM参数对调制性能影响很大，存在以下规律：调制指数h影响CPM频谱特性，h越小，频带利用率越高；关联长度L越大，接收信号检测的正确性越高，但计算量及解调复杂度急剧上升；多进制数M增大，每个信息符号携带的比特数越多，会使得信息传输的比特率得到提高，但同时也会带来误码率性能的下降。除进制数M，调制指数h相互影响外，其他参数相互独立，选择相关参数时，要考虑效率与效果的匹配，尽量做到兼顾。选择合适的参数会让系统性能最优，同时也可使检测和解调复杂度最优。