基于最近航迹迭代的目标航迹对准关联算法

宋 强 周万宁

（海军研究院 北京 100037）

1 引言

雷达对目标进行探测时不可避免地存在着探测系统误差［1］，在雷达组网系统中，可靠地目标航迹关联需要首先对系统误差进行准确估计［2～3］，而准确估计系统误差又建立在可靠获得航迹关联基础上［4～5］。因而，在精确系统误差配准和可靠航迹关联之间就存在着互为前提和条件的矛盾问题。

为此，人们对雷达存在系统误差情况下的目标航迹关联问题（本文称其为航迹对准关联问题）开展了一些研究［4～9］。由于雷达系统误差只是使得各雷达目标航迹间发生一定程度的整体旋转和平移，而未对目标间的拓扑结构产生影响，基于此，文献［4～7］利用拓扑信息或关系来研究解决上述问题，但这些方法仍存在众多限制条件。

为解决上述问题，借鉴图像匹配中广泛应用的最近点迭代（ICP）思想，本文构建基于最近航迹迭代（ICT）的航迹对准关联算法。

2 ICP基本思想

ICP算法是一种刚体图形匹配算法，其是由Besl和McKay于1992年提出的［10］，目前已在计算机图形匹配与医学图像配准中得到了广泛的研究和应用［11～13］。

假 设 图 形 点 集 A={a1,a2,…,ap}和B={b1,b2,…,bq}之间存在旋转和平移刚体变换。

定义第l步时的点集为 Al（l=0,1,2,…，且A0=A），假设在l-1步时已经获得一组平移和旋转估计分别为且对于每个点。而在第l步时，对于各点，在B中寻找距离该点最近的点，使得其满足

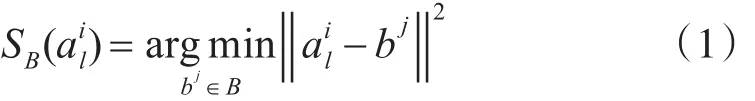
其中‖‖·表示欧氏统计距离。

定义B中满足上述最近邻准则的所有点构成新的点集为SB(Al)，则有

SB(Al)也表示第l步时点集 Al中所有点在B中最近点的集合，且集合SB(Al)与Al中的点构成一一映射，即点。

假设l时刻Al和SB(Al)间仍然存在某种残余的旋转R与平移T，定义代价函数，也即变换后图形点集间的第l步不相似度为

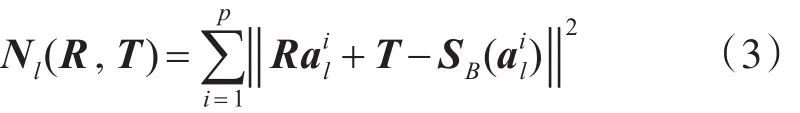
通过最小化代价函数Nl(R,T)，可获得此变换关系下刚体变换参数R和T的最优估计

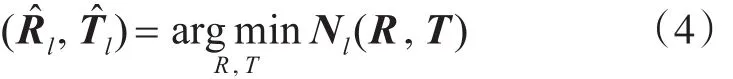
也即表示在旋转 Rˆl与平移Tˆl下，图形点集 Al和SB(Al)具有最大相似度。

3 基于ICT的航迹对准关联算法模型

3.1 系统描述

假设由两部二坐标雷达A、B组成雷达组网系统，雷达A和雷达B在笛卡尔坐标系中的坐标分别为（0，0）、(xBs,0)；两雷达的测距系统误差分别表示为ΔrA、ΔrB，而测方位角系统误差分别为ΔθA、ΔθB。

假设雷达A、B的上报目标航迹号集合分别为UA={1,2,…,nA}，UB={1,2,…,nB}，其中，nA、nB分别为两雷达上报航迹数。设在公共笛卡尔坐标系中，两雷达上报航迹中对应于同一目标的k时刻位置状态估计分别记为

在雷达存在系统误差情况下，两雷达的上报目标航迹间将产生旋转和平移，这里假设两雷达航迹间的旋转量为φ，而平移量为(Tx,Ty)，则两雷达目标状态间存在以下刚体变换关系

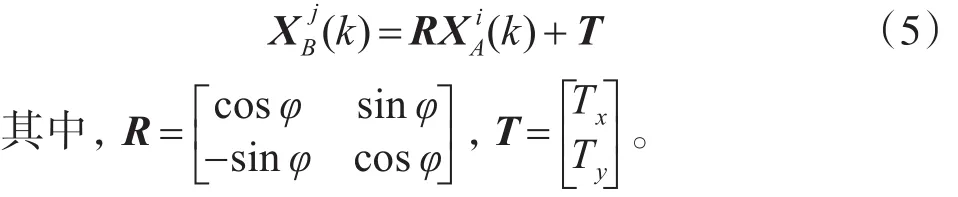
3.2 航迹关联映射搜索

由于雷达存在系统误差时将造成目标航迹发生整体旋转和平移，在这种情况下对目标航迹进行对准关联，也可归纳为对目标航迹间进行匹配对准以及搜索航迹相互映射关系的问题，因而可借鉴ICP思想来进行目标航迹对准关联。

为此，定义雷达A、B的航迹集分别为

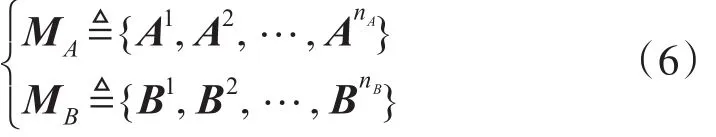
其中 Ai、Bj（i∈UA，j∈UB）分别表示雷达A、B航迹集中第i、j目标航迹，且

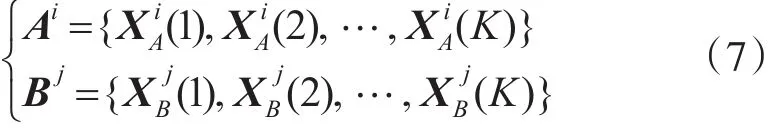
假设在第l步时，已经获得前l-1步的平移和旋转估计 Rˆs（对应 φˆs）和 Tˆs（ s=0,1,2,…l-1）。定义经第l-1步平移和旋转后获得的航迹集为，那么，对于每条航迹，经第l-1步平移和旋转后将得到航迹，其中航迹点表示为，因而有

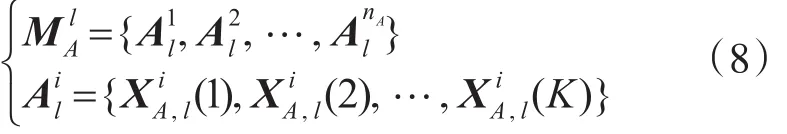
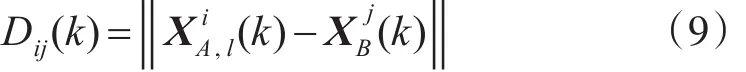
由于系统误差通常不会过大，也可获知系统误差的大致范围，因而可根据该信息定义雷达目标航迹间的距离阈值为Dmax，即若来自雷达A、B的k时刻目标点迹间的欧氏距离满足Dij(k)≤Dmax，且在所有满足该条件的航迹点中为最近邻点，则认为两航迹点可能来自同一目标，即k时刻两目标航迹点试验关联成功。

而∀k=1,2,…,K，取正整数I，在各时刻检验过程中，利用计数器mij(k)计数，如果k时刻两雷达的目标航迹点试验关联成功，则计数器加1，即mij(k)=mij(k -1)+1，(mij(0)=0)。

而若在L次关联检验完成后，计数器所计值满足mij(L)≥I，则判决航迹为可行关联对，也即存在可能映射关系。如果∀j∈UB都有mij(L)＜I，则认为雷达B航迹集内无与航迹可关联航迹。

将满足MB中上述意义下与相关联的航迹表示为

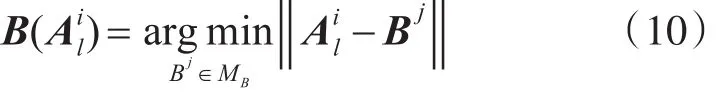
3.3 平移与旋转参数估计

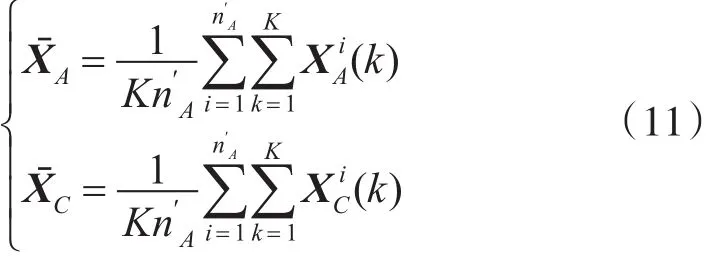
这样，代价函数可化为

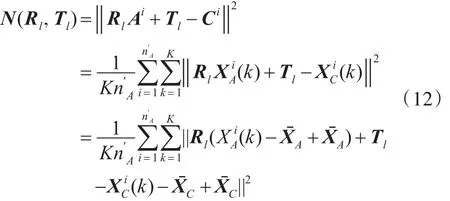
记

则经过展开，式（12）可表示为

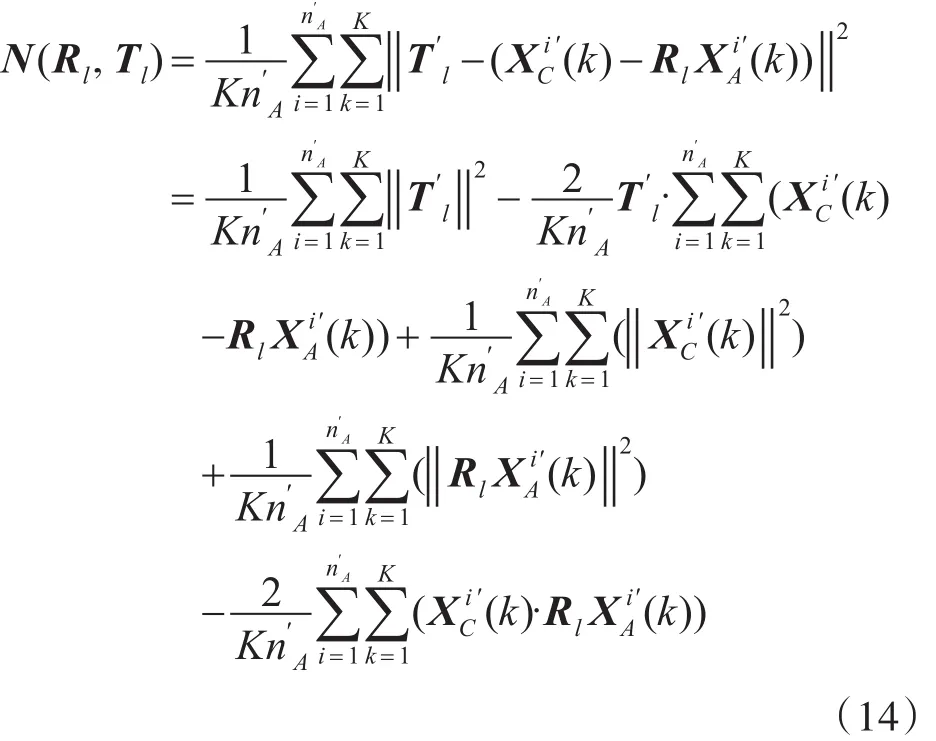
结合式（11），可知上式第二项中

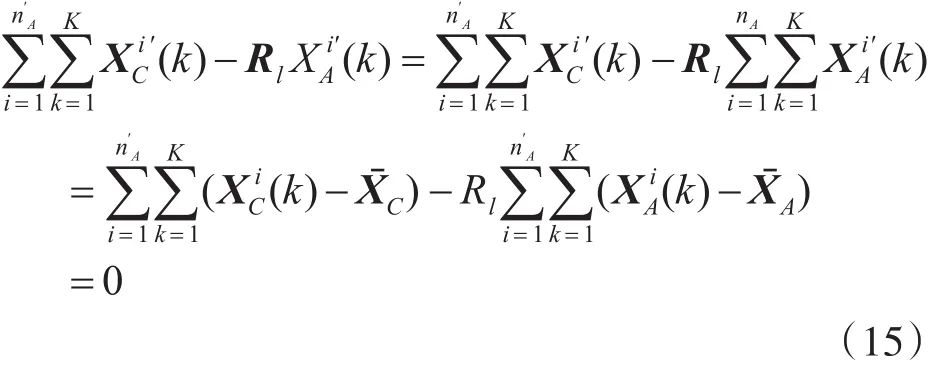
关系时，能够使得代价函数最小化。

而将下式带入式（14）

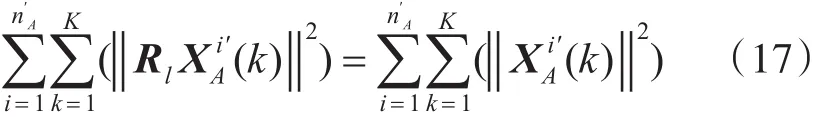
则第三、四项均与旋转变换无关。

因此，式（14）仅需考虑最后一项，令

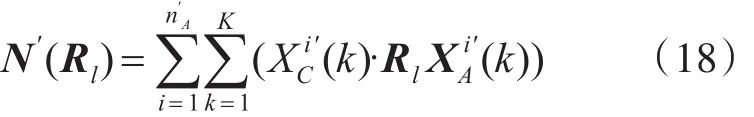
这样，为使得原代价函数N(Rl,Tl)最小，需要使得N′(Rl)最大化，也即求取使得其最大化的旋转变换 Rˆl或其对应的旋转角 φˆl。

展开式（18），有

为使上式取极大值，不难获得第l步φl的估计值为

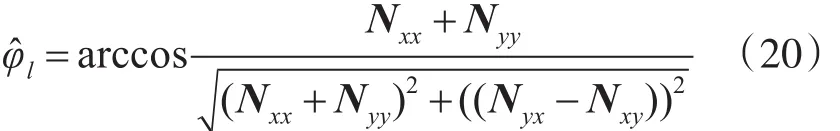
而相应的平移变换 Tˆl则可结合估计值 φˆl，根据式（16）求得。

3.4 ICT对准关联算法流程

综上，ICT航迹对准关联算法采用上述航迹关联映射关系搜索与平移旋转参数估计两步迭代进行，其基本流程简要可描述如下：

1）初始化

2）获取映射航迹集

3）更新旋转与平移变换

各航迹之间的对应关系不变的情况下，利用3.3节所述方法计算使第l步代价函数N(Rl,Tl)最小的变换估计，并令其为(Rˆl,Tˆl)，参与下一步迭代；

4）终止与迭代

当迭代步数超过一预先给定数时，亦终止迭代更新，宣布对准关联失败。

否则，继续2）、3）步，迭代更新映射航迹集与旋转与平移变换参数。

假设算法在第L步终止迭代，则航迹集间旋转角和平移量最终估计分别为

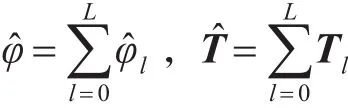
4 算法仿真分析

假设由两部2D雷达A、B所构成的雷达组网系统，两部雷达的坐标分别为（0，0）、（150km，0）。两雷达均具有测距100m、测角1°的随机量测误差，分别具有测距1km、测角1°与测距1km、测角-1°的探测系统误差。

目标在一个两维平面上进行匀速直线运动，具有可以认为在速度上变化的过程噪声，初速和初始航向分别在30m/s～80m/s和0prad～2prad之间均匀分布。各批目标的初始位置分别在由（65km，65km）、（65km，85km）、（85km，85km）、（85km，65km）四个端点所划分的矩形区域中按均匀分布产生。

设定蒙特卡洛仿真次数设为100次，仿真时长为150s。在以下四种环境中进行三个算法的仿真比较：

环境1：假设进入两雷达公共观测区域的目标数设为20批，且其中存在5批相互间距设置为1km的编队目标；

环境2：假设进入公共观测区域的目标数设为40批，且其中存在10批相互间距设置为1km的编队目标；

环境3：假设进入公共观测区域的目标数设为20批，且其中存在5批相互间距设置为1km的编队目标；两部雷达均存在对目标的漏跟现象，且都设定为各存在对1批目标的漏跟，而两雷达漏跟目标不对应同一目标；

环境4：假设进入公共观测区域的目标数设为40批，且其中存在10批相互间距设置为1km的编队目标；两部雷达均存在对目标的漏跟现象，且都设定为各存在对1批目标的漏跟，而两雷达漏跟目标不对应同一目标。

假设各算法仿真所得正确、错误及漏关联航迹对总数分别为Nc、Ne及Ns，本文中定义航迹正确关联概率为Ec=Nc/(Nc+Ne)、航迹错误关联概率为 Ee=Ne/(Nc+Ne)、航迹漏关联概率为Es=Ns/(Nc+Ne+Ns)。

仿真结果如下表1所示，给出了在上述四种仿真环境中（为简便起见，表1中“环境”将用“Env”代替），采用ICT算法与采用文献［2］、［7］以及文献［9］算法的航迹正确、错误及漏关联概率。

通过对在4种环境中各算法结果的对比不难看出，本文所提ICT算法所获得的关联效果均最好。其中，在环境1、2中，由于雷达对目标的良好跟踪效果，各算法都能获得很好的目标航迹关联效果，但ICT算法所获得的正确关联概率最高，文献［9］算法的性能稍差，且两种算法均没有漏关联的现象；相比而言，文献［2］、［7］算法的性能最差，但航迹正确关联也达到了90%以上，该算法漏关联概率较高。而在环境3、4中，由于两部雷达都存在对目标的漏跟现象，使得本文算法的正确关联概率比环境1、2概率有所下降，但也只相应下降了两个百分点左右，其关联性能仍是几种算法中最好的。这是由于本文算法在设计时，已经有效地考虑了雷达对目标漏跟或虚警等情况，所以能够保证算法性能下降不大，且亦能获得很高的正确关联概率。但是同等条件下，其它文献算法所得的正确关联概率下降幅度非常大，基本已经不能获得正常的航迹关联效果，说明这些算法对目标漏跟以及虚警情况的严重不适应性。。

通过对在环境1、3与环境2、4中的各算法关联概率的对比可以发现，这几种算法对于目标密度的影响均较小，说明这几种算法对于目标密度均有较好的适应性。

ICT算法仅经过几步迭代就能够获得最佳航迹映射关系，且在三种算法中耗时最少，没有出现因迭代次数超出规定次数而导致对准失败的现象，这说明了本文算法具有良好的实时性。

5 结语

为解决在雷达网存在系统误差时的航迹关联问题，本文提出了一种基于最近航迹迭代的目标航迹对准关联算法。

由蒙特卡洛仿真结果对比可得，本文算法在雷达存在系统误差、密集目标以及雷达存在对目标漏跟等各种情况下均能取得很好的航迹对准关联效果，且具有算法结构简单以及工程实用性较强等特点。