基于改进空间平滑算法的复杂多信号测向技术研究
2018-10-23林彬
林 彬
(中国船舶重工集团公司第七二三研究所 扬州 225001)
1 引言
空间谱估计是阵列信号处理的重要研究方向之一,其以空间多传感器阵列为基础,通过先进的数字信号处理手段对空间信号的参数进行估计。由于其优越的波达角估计(DOA)性能,因而在雷达、电子侦察、声纳、通信等相关领域中都有着广泛应用[1~4]。
到目前为止,涌现出大量的DOA估计算法,如多重信号分类(MUSIC)法[5~6]、信号参数估计方法(ESPRIT)[7-9]等。这些算法在DOA 估计上有着非常高的测向分辨率,但这些算法都是建立在信号不相干假设的基础上,因此无法适用于相干的信号环境。而对于低角测向跟踪的舰载或地基雷达/电子侦察设备,经常会面临来自多路径效应带来的干扰信号,这些多径干扰信号与直达回波是相干的。尽管目前有人提出基于空间平滑算法的解决办法,但是该算法只适用于高斯白噪声环境,但在实际应用环境中,这样的假设并不总是成立的,大量色噪声的存在会使得该算法的性能急剧下降。此外,该算法要完成对N个相干信号源的测向,至少需要2N个阵元,并且在低信噪比条件下该算法的性能较差[10~12]。
针对空间平滑算法无法在有限阵元数目下实现多相干信号源的测向等问题,本文提出一种基于改进的空间平滑算法,该算法通过在前后向平滑算法中引入传播算子(PM)算法,一方面可以在色噪声环境获得优异的测向性能,另外该算法可以降低对阵元数目的要求,并且还适用于非相干、相干和混合信号源等的复杂多信号环境。
2 空间平滑MUSIC算法的基本理论
MUSIC是最经典的超分辨谱估计算法,它是首先对阵列接收数据的协方差矩阵进行特征值分解,把对应的特征矢量分成信号子空间和噪声子空间,利用两个子空间的正交性,对信号进行谱估计。
对于M元各向同性均匀线阵,阵源间距为d,当位于θk(k=1,2,...P)处有P个窄带点源。则各阵列接收的快拍数据为

式中 X(t)为 M×1快拍数据矢量,X(t)=[x1(t),......xM(t)]T。 N(t)为M×1阵列阵元噪声矢量,且是与信号源不相关的高斯白噪声,均值为 0,方差为,N(t)=[n1(t),......nM(t)]T。 S(t)为输入信号矢量S(t)=[s1(t),......sM(t)]T。 A(θ)为阵列的导向矢量矩阵,为
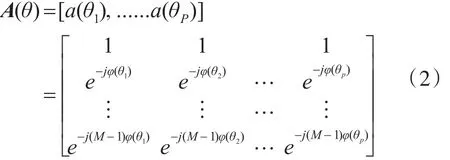
当空间信源互不相干时,对协方差矩阵R进行特征分解,构造信号子空间和噪声子空间,令其特征值分解

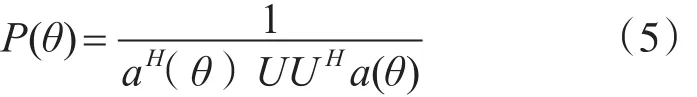
由于MUSIC算法是基于信号不相干的前提,因此无法完成对相干信号的DOA估计,为了解决这一难题,可以先通过空间平滑算法对信号进行去相干处理。具体为将天线阵列分成相互交错的P个子阵,每个子阵包含的阵元数为m个,即满足M=p+m-1。信号源数为N。
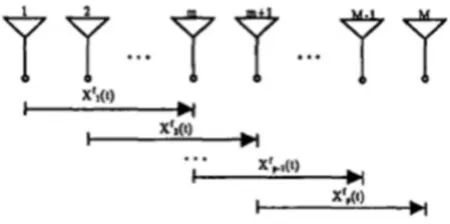
图1 空间平滑算法的原理图
如图1所示,取第一个子阵(最左边的子阵)为参考子阵,那么各个子阵的输出矢量分别为
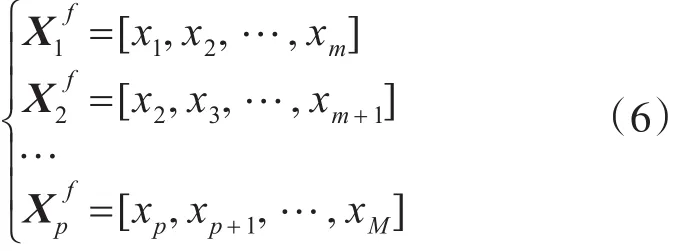
对于第k个子阵有:
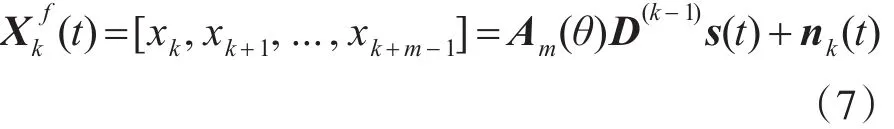
其中:
那么该子阵的数据协方差矩阵为
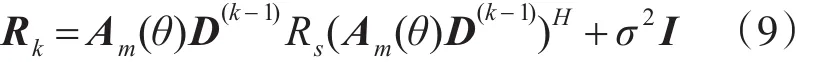
其中,Am是一个m×p的参考子阵(通常取第一个子阵)的导向矢量矩阵。
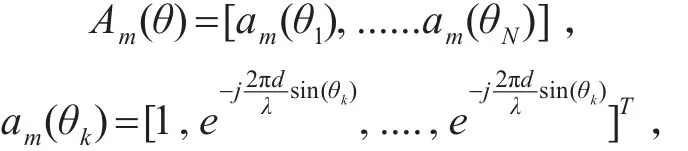
Rs为信号的协方差矩阵,Rs=E{ssH}。
前向平滑修正的协方差矩阵为

同理可得后向空间平滑修正的数据矩阵Rb,取前向平滑和后向平滑数据协方差矩阵的平均,即前后向空间平滑的数据矩阵,即

图2为天线阵元为8,相干信号源数目分别为3和5下,经典MUSIC和前后向空间平滑MUSIC算法的DOA估计功率谱。
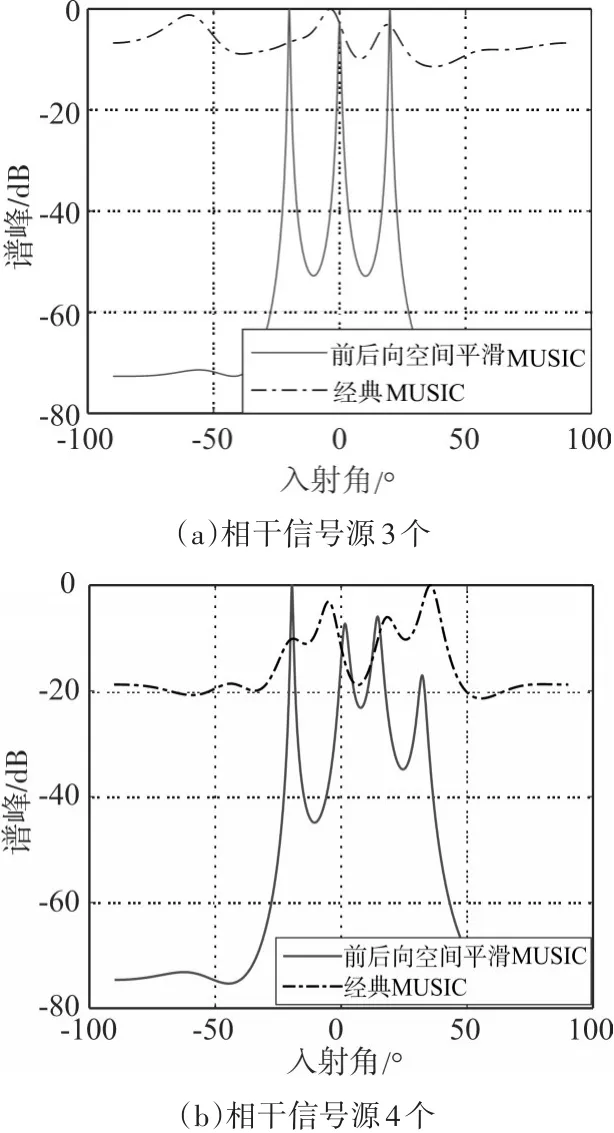
图2 DOA估计的功率谱
由图2可以看出,在相干信号源的情况下,经典MUSIC无法形成正确的功率峰,在相干信号源数目为3时,前后向空间平滑MUSIC算法能给出了精确的DOA估计,但当相干信号源为5时,前后向空间平滑MUSIC算法DOA估计的性能急剧下降,估计的角度只有两个正确,其他均出现偏差,这是由于该算法要完成对N个相干信号源的测向,至少需要2N个阵元。
3 改进空间平滑MUSIC算法的基本理论
在色噪声环境下,式(1)的协方差矩阵可以写为
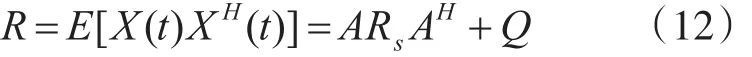
式中Q为噪声的协方差矩阵,Rs为信源的协方差矩阵。
阵列接收到的所有信号协方差矩阵的估计值为
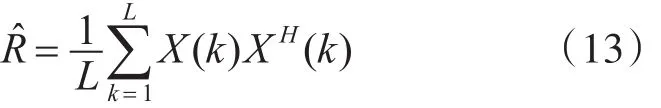
当R满足正定矩阵矩阵,也即式(14)成立:

式中J为变换矩阵,它的反对角线对应数值为1,其他数值为0,*为复共轭。
在这里我们仍然沿用前后向空间平滑算法,这样子处理主要是将快拍数据量加倍和去相关,此时前后向空间平滑处理后的协方差矩阵为
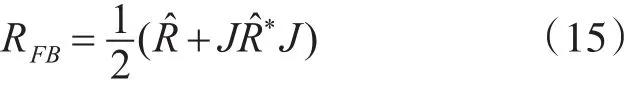
对于协方差为对称Toeplitz矩阵的噪声,前后向协方差矩阵RFB与后向协方差矩阵的厄米矩阵之差为
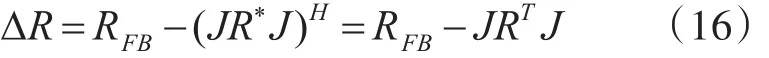
将式(12)、式(15)代入上式整理可得:
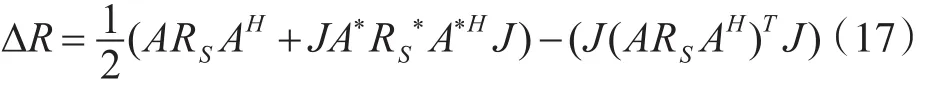
引入传播算子(PM)算法,可以将式(17)写为以下形式:

其中G和H分别代表ΔR的前K和后M-K列:
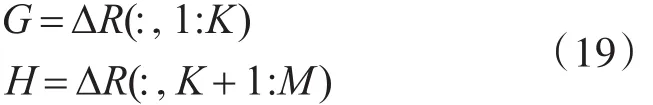
因此存在线性算子F使得下式成立:

因此,有:

其中,G#为广义逆矩阵,G#=(GHG)-1GH。
此时存在M×(M-K)矩阵E:

使得

其中I(M-K)为M-K维单位矩阵。
阵列的导向矢量矩阵可以写成:

最终可以得到信号的功率谱为[14~15]

上式中E不是在传统的子空间方法中使用的噪声子空间的任何特征向量,因此,所提出的方法不需要任何特征分解,其复杂度小于子空间方法。
4 改进空间平滑MUSIC算法的数值仿真
为了对比分析改进空间平滑MUSIC算法和前后向空间平滑MUSIC算法的性能,下面对天线阵元为8,信号源数目为6,针对色噪声环境下全为非相干信号、全为相干信号、非相干和相干混合信号等三种情况进行仿真,其中6个信号源的空间位置分别为[20°、30°、40°、50°、60°、70°]。
1)非相干信号源的仿真
图3为6个信号源相互独立,非相干情况下,信噪比分别为-10dB和15dB下DOA估计的功率谱。
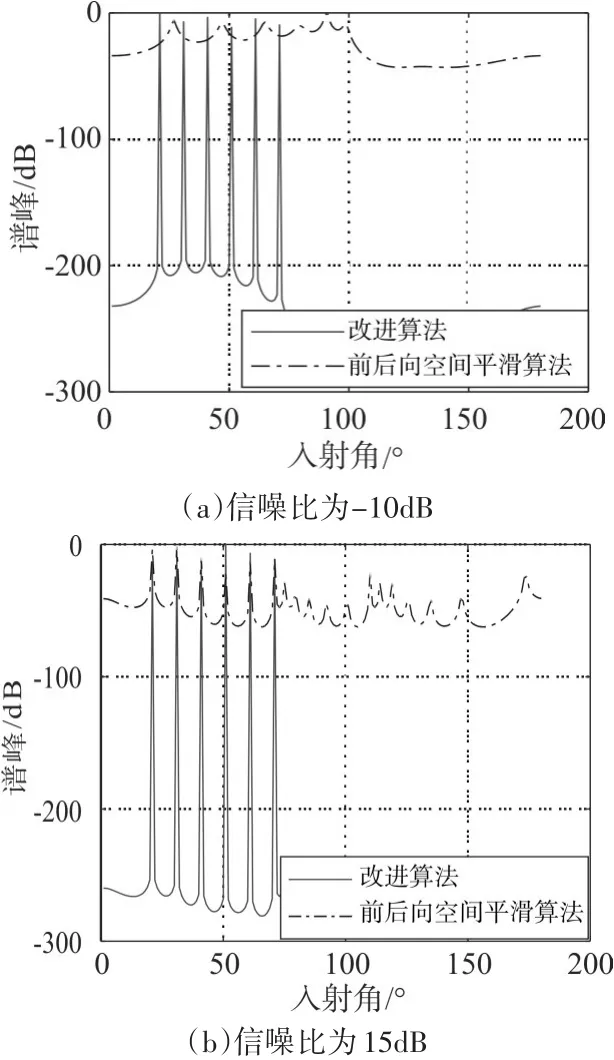
图3 非相干信号源下的DOA估计功率谱
由图可以看出,改进空间平滑MUSIC算法对六个非相干信号源都能给出了精确的DOA估计,在 20°、30°、40°、50°、60°和70°上形成六个尖锐的峰,并且在信噪比较低时也能获得非常好的检测性能。而前后向空间平滑MUSIC算法只能在信噪比为15dB时才能检测六个信号源,谱峰不够尖锐,当信噪比降低到-10dB时,该算法无法检测到目标正确位置,这是由于低信噪比和阵列数量不足导致的。
2)相干信号源的仿真
图4为6个信号源为相干信号源,这种情形在多径反射时经常存在,其信噪比分别为-10dB和15dB下DOA估计的功率谱。

图4 相干信号源下的DOA估计功率谱
由图可以看出,改进空间平滑MUSIC算法对六个相干信号源都能给出了精确的DOA估计,在20°、30°、40°、50°、60°和70°上形成六个尖锐的峰,并且在信噪比较低时也能获得非常好的检测性能。而前后向空间平滑MUSIC算法只能在信噪比为15dB时才能检测六个信号源,谱峰不够尖锐,当信噪比降低到-10dB时,该算法无法检测到信号源正确位置,这是由于低信噪比和阵列数量不足导致的。
3)混合信号源的仿真
图5为6个信号源为混合信号源,其中2、3、4、5为相干信号源,1和6与之不相干且互不相干的信号源,为这种情形在实际环境中也经常存在,其信噪比分别为-10dB和15dB下DOA估计的功率谱。
由图可以看出,改进空间平滑MUSIC算法对六个混合信号源都能给出了精确的DOA估计,在20°、30°、40°、50°、60°和70°上形成六个尖锐的峰,并且在信噪比较低时也能获得非常好的检测性能。而前后向空间平滑MUSIC算法在混合信号源的情况下,在信噪比为15dB时,也无法形成正确的功率峰,即在混合信号源下该算法无法检测到目标正确位置。
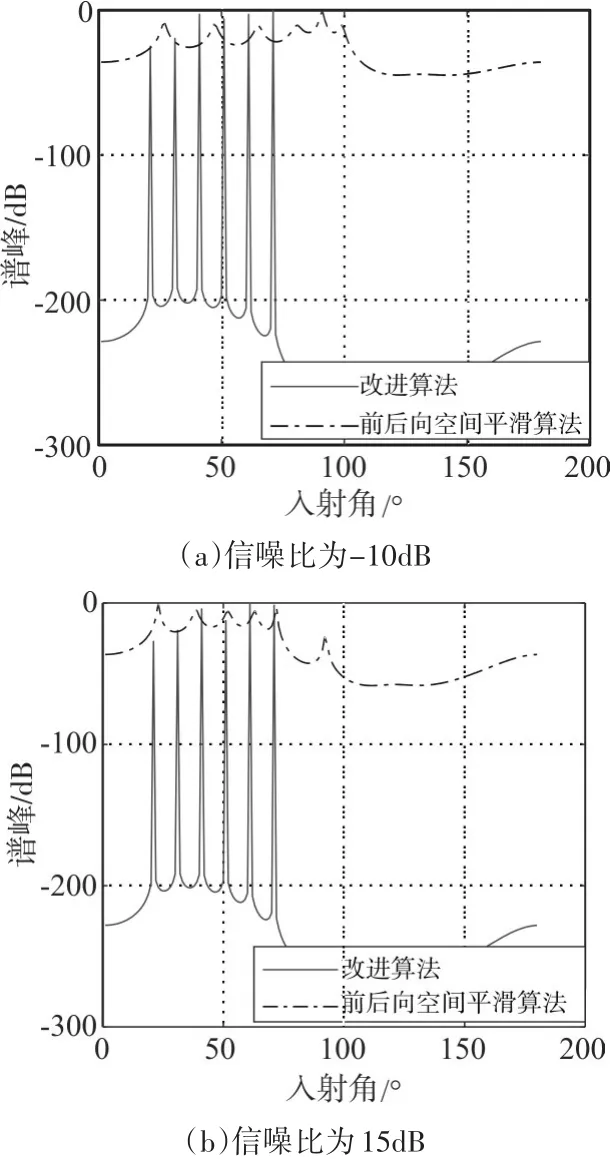
图5 相干信号源下的DOA估计功率谱
5 结语
本文针对空间平滑算法无法在有限阵元数目下实现多相干信号源的测向等问题,提出一种基于PM的改进空间平滑MUSIC算法,该算法降低DOA估计对阵元数目的依赖,仿真结果表明该改进算法可以适用于非相干、相干和混合信号源等的复杂多信号环境。
