基于WEKA平台的决策树算法比较研究

杨小军 钱鲁锋 别 致

（国防大学联合勤务学院后勤与装备信息资源教研室 北京 100858）

1 引言

决策树算法是数据挖掘领域广泛研究和应用的一种分类算法，具备计算量小、速度快、分类准确率高、分类规则容易被人理解等优点，主要的决策树算法有ID3、C4.5、CART、SLIQ、SPRINT等。在数量众多的决策树算法中，不同的决策树算法在处理数据类型、建模机制的选取、决策树构建方法、分类规则表达方式等方面存在很大的区别。对于这些各具特色的算法，该如何比较和评定它们的性能好坏呢？用来比较和评估决策树算法性能优劣的指标主要有以下五个［2］：

l）预测准确率。模型正确地预测数据类别的能力；

2）速度。产生和使用模型的计算时间花费；

3）强壮性。模型对数据包含噪声或有空缺值时正确预测的能力；

4）可伸缩性。对于大型数据集，能有效构造模型的能力；

5）可解释性。模型是否易于理解。

WEKA是新西兰Waikato大学开发的数据挖掘系统，实现了基本的决策树分类算法，提供了适用于各类数据集的数据预处理以及算法性能评估方法，具有很强的扩展性和兼容性。本文对WEKA平台中的三个经典的决策树算法C4.5、CART和NBTree算法进行算法性能分析和比较。

2 三种决策树算法实现原理

用决策树算法对训练样本数据集进行挖掘后会生成一棵形如二叉树或多叉树的决策树。该决策树的叶子节点代表数据的某一类别，非叶节点代表某个非类别属性的一个判断，判断的一个结果形成非叶节点的一个分枝，从根节点到叶子节点的一条路径形成一条分类规则。如此一棵决策树就能够转化为若干条分类规则，再根据这些生成的分类规则就可以快速地对未知类别的数据样本进行预测。构造一棵决策树的通用算法描述如下［3］：

BuildDecisionTree（Training Dataset E）

if（E满足某个中止条件）Then return；

For（i=l；i＜=E中属性的个数；i++）

评估每个属性关于给定的属性选择度量的分裂特征；

找出最佳的测试属性并据此将E划分为E1和E2；

BuildDeeisionTree（E1）；

BuildDeeisionTree（E2）；

EndIf

算法的终止条件一般有三种情况［3］：

1）训练数据集E中所有的样本都属同一个类，则将此节点当作一个叶子节点，并以该类标记此节点；

2）无属性可以作为测试属性；

3）训练样本的数量少于用户提供的阈值。

后两种情况中一般以训练样本中占优势的类标记该叶子节点。属性选择度量有信息增益、信息增益率和Gini指数等。通常，一棵能完全分类训练样本集的决策树并不是最好的，因为这样的树对训练样本集过于敏感，而训练样本集均无可避免地存在噪声和孤立点。需要对生成的树进行剪枝，以去除过分适应训练样本集的枝条，避免过拟合现象产生。C4.5、CART和NBTree三种决策树分类算法的不同之处在于属性选择标准各异。

2.1 C4.5算法

C4.5决策树算法是基于ID3算法改进而来的，假设样本集E分为C类样本训练集，每类样本数量为 pi，i=1，2，…C。如果用属性A为测试属性，属性A的v个不同的值分别为{v1，v2，…vv}，用属性A将样本集E划分为v个子集{E1，E2，…Ev}，假设Ei中含有第j类样本数为 pij，j=1，2，…C，子集 Ei的熵为

属性A的信息熵为

一棵决策树对一样例作出正确类别判断所需要的信息为

属性A的信息增益为

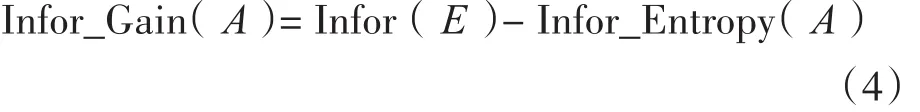
信息增益是ID3算法的属性选择标准，ID3算法具有存在着只能处理离散属性，构造的决策树与数据之间容易过拟合，对噪声敏感等问题。在ID3算法的基础上进行改进形成以信息增益率为属性选择标准的C4.5算法。属性A的信息增益率计算如下：

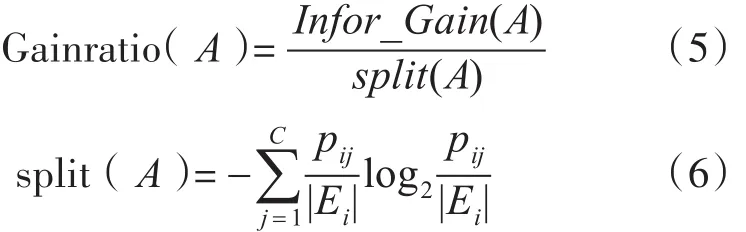
C4.5算法以信息增益率为标准决定决策树分支的准则，寻找最佳分组变量和分割点，从而建立决策树。其具备分类规则易于理解、算法复杂度低等优点。C4.5算法克服了ID3算法属性偏向的问题，增加了对连续属性的处理，通过剪枝，在一定程度上避免了过拟合现象。但是该算法将连续属性离散化时，需遍历该属性的所有值，效率有所降低。

2.2 CART算法

CART算法全称为分类回归树，既可以处理分类问题又能处理回归问题，本文只关注其处理分类问题的能力。CART算法进行分类时采用Gini指数作为测试属性的选择标准。Gini指数计算如下：

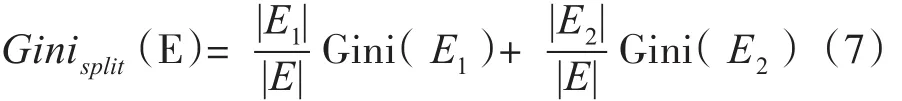
其中 |E|，|E1|，|E2|分别是样本集E、E1和 E2中的样本个数。

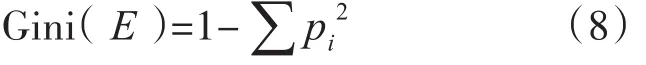
其中 pi是类别i在样本集E中出现的概率。CART算法生成的决策树精度较高，但随着决策树复杂度的提高，分类精确度会有所降低，用该算法建立的决策树不宜太复杂。

2.3 NBTree算法

NBTree算法是朴素贝叶斯和决策树算法两种分类技术的融合，提取了两种算法的优势。该算法在树的构建过程中，对产生的每个结点构建朴素贝叶斯分类器，并循环这个过程，直至所有结点都成为叶子结点，最后对每一个叶子结点都构建一个朴素贝叶斯分类算法。NBTree算法的分类标准为，对于属性（A1，A2，…，An），计算各属性 Ai的效用μ（Ai），取得效用最高为μ的属性。当μ不能显著优于当前结点的效用时，则为当前结点构造一个朴素贝叶斯分类算法，再返回。根据各属性上的效用测试来划分样本集。NBTree算法优点为，首先，算法过程清晰、直观；其次，在计算复杂度不高的前提下能保持较高的分类正确率。

3 算法性能分析实验

本文试验中的数据来自于UCI数据集，UCI数据集是美国加洲大学尔湾学院公开的科研数据集，本文从UCI数据集中选取了8个样本数据集，用于决策分类算法的比较分析，这些数据集需要经过简单的预处理：去除具有唯一值的ID和Name属性，将序数型的类标转化为标称型。完成预处理后的数据集基本信息如表1所示。使用WEKA平台中现有的 C4.5（J48）、CART（SimpleCart）和 NBTree算法对实验数据集进行分类，实验采用10折交叉验证法。实验机器选用联想台式机，具体配置：处理器为Intel i5-4590 3.30GHz处理器；4G内存；64位windows操作系统。实验最终的结果体现在表2、表3、表4和表5四个表格中。

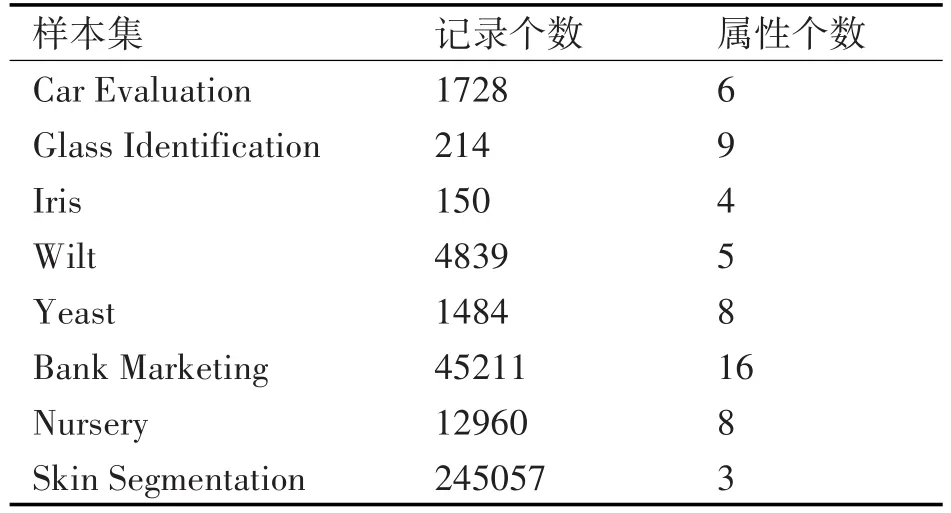
表1 WEAK平台下决策树算法性能分析实验数据基本信息

表2 算法分类准确率比较

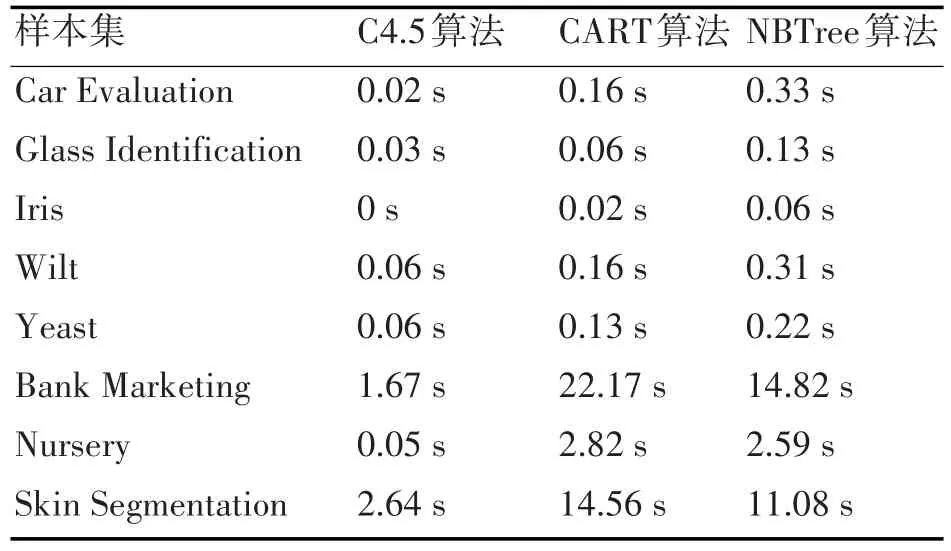
表3 算法建模时间比较

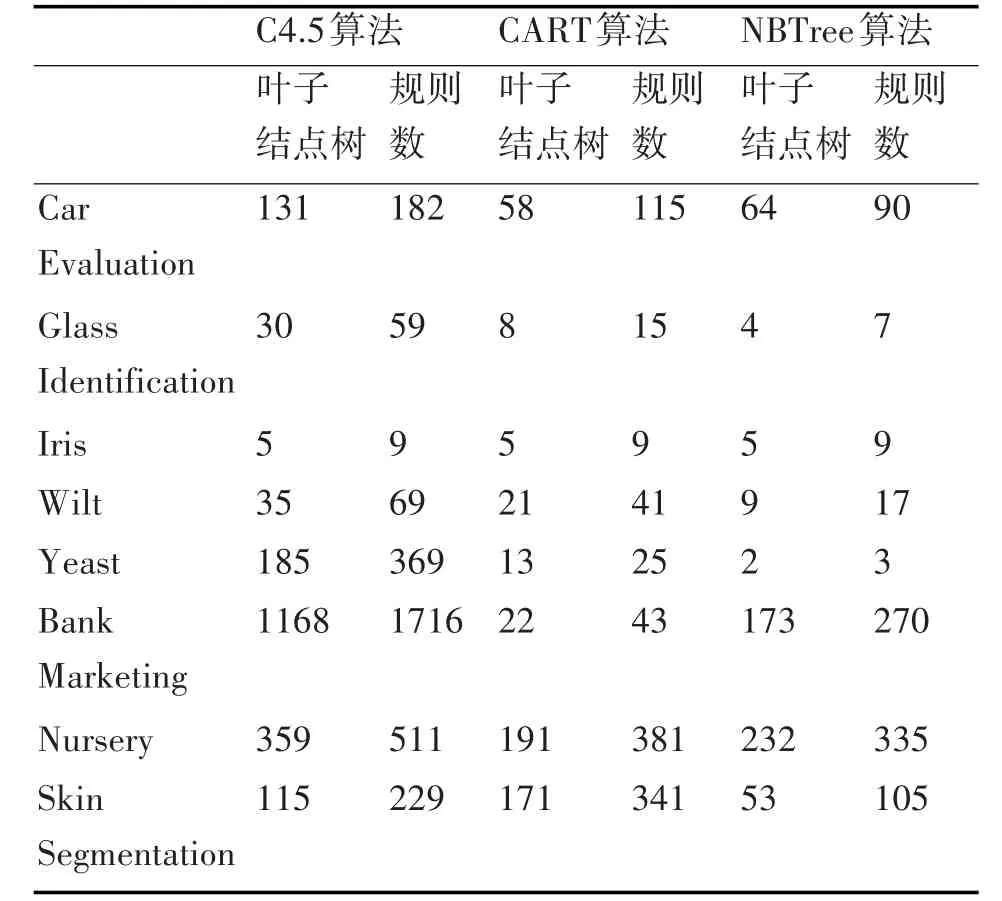
表4 算法生成决策树情况

表5 规则数目与叶子节点数目的比值情况

4 实验结论分析

根据表3的实验结果，从建模速度来看，大部分情况下，三种算法中C4.5算法的建模速度最快，CART算法建模速度次之，NBTree算法建模速度最慢。但在 Bank Marketing、Skin Segmentation、Nursery三个数据集上，NBTree算法建模速度要优于CART算法，在Bank Marketing和Skin Segmentation这两个数据集上表现得更明显，原因于这三个数据集的记录数量分别为45211、245057、12960，是实验所用的八个数据集中最大的三个，随着数据集中数据量的增长，CART算法的建模速度有所下降，不及NBTree算法。

从分类的效果来看，依据表2，大部分情况下，CART算法准确率最高，NBTree算法次之，C4.5算法准确率最低。个别情况下，如在Iris和Skin Segmentation两个数据集上，C4.5算法无论建模速度还是分类准确率都是最好的。从表1我们可以看出，Iris数据集的属性数量只有4个，Skin Segmentation数据集的属性数为3，数据之间的关系相对简单，C4.5算法在简单数据集上的分类准确率比NBTree算法和CART算法都要高。

一个算法，如果能以较少的叶子结点生成较多的规则，则算法的可解释性强，根据表5，当数据量不大且数据之间关系相对简单时，C4.5算法的可解释性最好，CART算法次之，NBTree算法的可解释性最差。当数据量和数据的复杂程度提高时，CART算法的可解释性最好，C4.5算法次之，NBTree算法的可解释性仍旧最差。以上是三种算法的总体情况，由于进行比较的八个数据集都是成熟的公开科研数据集，数据集规模不大，只有个别的数据集有少量的噪声数据，本文没有从可伸缩性和强壮性方面来对这三个算法进行实验比较。

5 结语

C4.5算法、CART算法和NBTree算法是三种经典的决策树分类算法，面对不同的数据集时，分类准确率、建模速度和可解释性都在发生变化，因此不存在可以解决所有分类问题的理想算法，进行分类时，需要根据数据集的情况，具体问题具体分析，选择合适的算法。当数据量不大或是数据关系比较简单时，优先采用C4.5算法。当数据量增长或是数据关系比较复杂时，优先采用CART算法，NBTree算法可以作为替补。本文讨论的三种算法均是基于内存构造树，针对的是百万条记录以下的数据集，在大规模数据情况下，需要加以改进，增强算法的可伸缩性。