一种改进的多基线相位干涉仪解模糊算法

居 易,张学成,邵文建

(中国船舶重工集团公司第七二三研究所,江苏 扬州225101)

0 引 言

无源定位技术是电子战侦察系统中的关键技术,而对辐射源的精确测向是实现准确定位的前提条件,因此精确测向对电子战侦察系统具有非常重要的意义。在现有的测向体制中,干涉仪测向具有精度高、结构简单、观测频带宽的优点[1-3]。受阵元本身物理尺寸的限制,在最小半波长的空间内无法安装2个阵元,只能采用阵元间距大于半波长的几何配置,并且多基线相位干涉仪测量相位存在周期性,因此会带来相位干涉仪的相位差模糊问题[4]。如果在解相位模糊时得到错误的模糊数,会导致测向误差超差,因此解模糊是多基线相位干涉仪测向的关键问题。

本文基于参差基线解模糊算法原理[5],利用最长基线鉴相精度,提出了一种解模糊的改进算法。与传统的解模糊算法相比,其具有计算量较小、适合实时计算以及正确概率较高的优点,适合工程应用。

1 多基线干涉仪测向原理

设N元天线组成的一维相位干涉仪阵列[6]如图1所示,相邻阵元间的基线长度分别为D1,D2,…,Dn,雷达信号的波长为λ,则基线Dn的相位差Φn为:

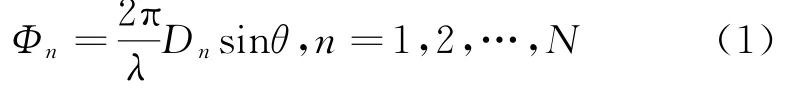
当Dn＞λ/2时,会出现相位模糊,理论测量相位差ϕn为:

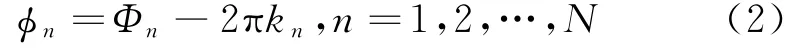
式中:kn为基线Dn的模糊数。

通过相位差Φn,就可以得到信号的入射角θ。测量相位ϕn在[-π,+π]范围内变化,由于相位差是以2π为周期,超过该范围,将出现多值模糊。

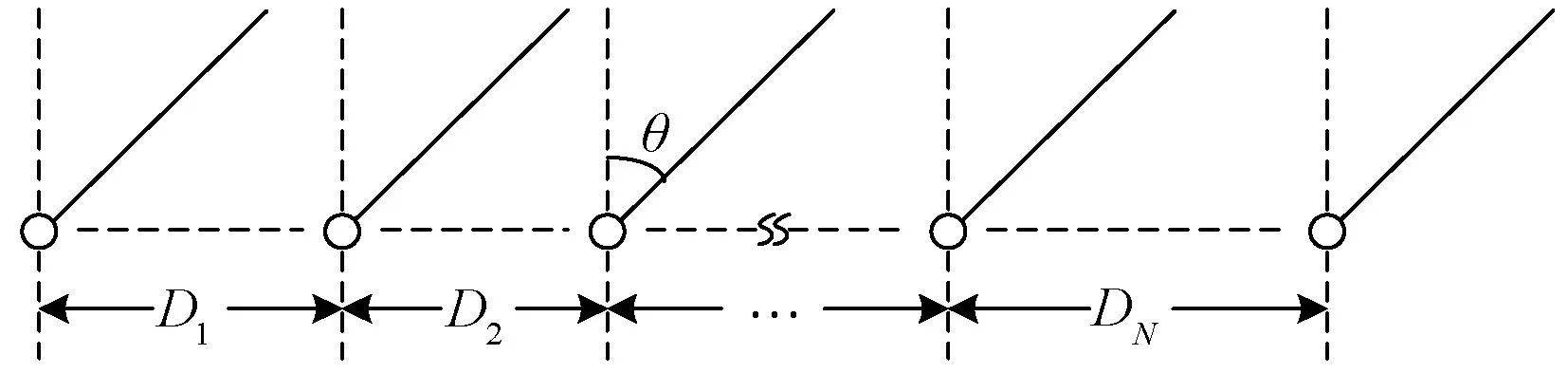
图1 一维相位干涉仪阵列示意图

入射角θ为:

天线单元间的基线长度Dn为基本基线长度d的整数倍,假设基线长度Dn=pnd,n=1,2,…,N,则有:

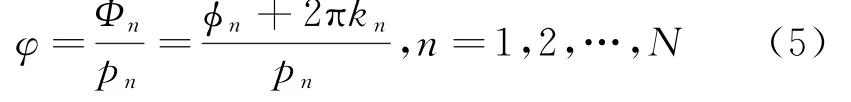
式中:kn取值范围为0,1,…,pn-1。

因此需要求解kn,计算基本基线相位差φ,从而计算入射角θ。

2 传统的干涉仪解模糊算法

2.1 逐级解模糊算法

逐级解模糊算法是一种经典的算法,主要原理是依靠较长基线的相位精度,并通过较短基线来解算较长基线的模糊值,算法要求每一步计算基线比例都为整数,并且最短基线为基本基线,不存在相位模糊,Φ1=ϕ1。

逐级解模糊算法简洁,计算量小,缺点是未充分利用所有基线参与解模糊计算[7],容差能力较差。在实际工程应用中,天线间距往往大于λmin/2,需要采用虚拟基线,使容差变小,解模糊错误概率较高。

2.2 参差基线解模糊算法

当存在噪声时,可以在最小二乘准则下对式(2)构成的方程组进行N-1维整数搜索[5],求得各个模糊数,具体计算公式为:

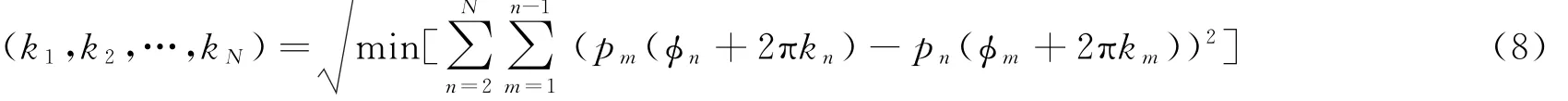
由于相位差Φn在[-πpn,+πpn]范围内变化,因此:

各个基线长度比值须满足:

该方法是满足最小二乘准则下的最优解,正确概率高,然而当天线阵元较多时,计算量大,无法实时计算。

3 改进的解模糊算法

考虑各个基线测量的相位差,则式(2)改写为:

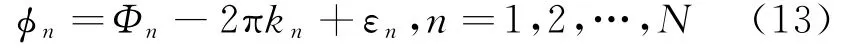
式中:εn为测量相位误差,服从相同的概率分布。

对于每个基线计算基线相位差,则:

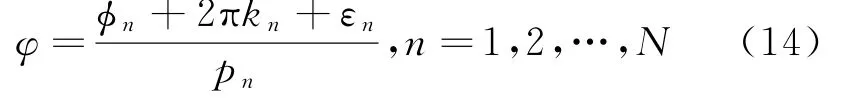
因此,当基线长度越长,pn越大,基线相位差φ计算误差越小,从而入射角θ计算误差越小。所以传统的干涉仪解模糊算法,无论是式(7)还是式(12),均以最长基线的相位差来计算,其中式(12)是以所有基线的长度之和作为最长基线。

基于参差基线解模糊算法原理,引入基线长度之和作为最长基线,记为D,为基本基线长度的P倍,模糊数为K。并记到达基线D的相位差为Φ,理论测量相位差为ϕ,测量相位误差为ε,则:

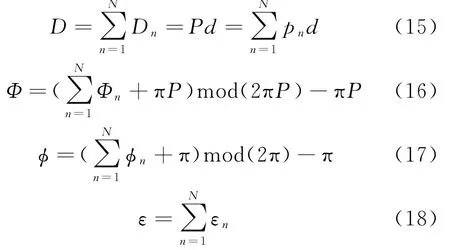
由于没有虚拟基线,最长基线测量相位误差ε与各个基线测量相位εn服从相同的概率分布。

由于相位差Φn在[-πP,+πP]范围内变化,因此:

因此K取值范围为:

则式(12)改写为:

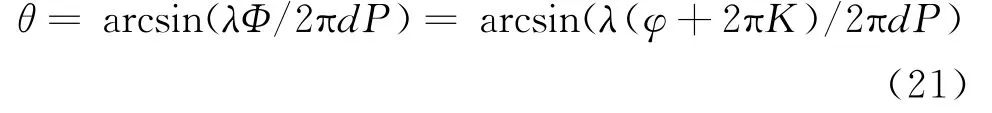
因此,只需要求得对K的正确估计,就能得到入射角θ。在最小二乘准则下对式(2)进行搜索,求得模糊数K,具体计算公式为:

kn取值范围满足式(10),K取值范围满足式(20)。

由于搜索维度相对式(8)低,因此式(22)的计算量远小于式(8)。并且式(22)由最小二乘准则下,对最长基线模糊值的最优估计,因此正确概率高,并且算法应用了最长基线的鉴相精度,测向精度高。

4 算法复杂度比较

下面来分析比较逐级解模糊算法、参差基线解模糊算法以及本文的改进干涉仪解模糊算法的复杂度。

对于具有稳定水位的透水性地层，地下水浮力可按理论静水压力进行计算，但是地下水的补给和地层的渗透性不同，实际地下水压力可能会低于静水压力值。因此，对于基底下的弱透水性地层来讲，采用排水抗浮设计时，要根据渗流定律对水压力值作适当折减。但是，该工程的地下室外墙回填土是粉质土，透水性高，补充了地下水，因此，水浮力采用静水压力计算还是比较合理的。

4.1 算法复杂度比较假设

假设逐级解模糊算法级数、参差基线解模糊算法基线个数、本文的改进解模糊算法基线个数相等,均为N。并且由于式(7)、式(12)和式(21)计算复杂度相当,且不属于解模糊的范畴,不参与比较。并且,加法与减法统一为加法运算,乘法、除法以及取模运算统一为乘法运算。

4.2 逐级解模糊算法复杂度

对于逐级解模糊算法每一步,根据式(6),需要2次乘法运算和1次加法运算。因此,逐级解模糊算法共计需要2N次乘法运算和N次加法运算。

逐级解模糊算法计算量非常小,适合实时计算。

4.3 参差基线解模糊算法复杂度

式(8)等价为:

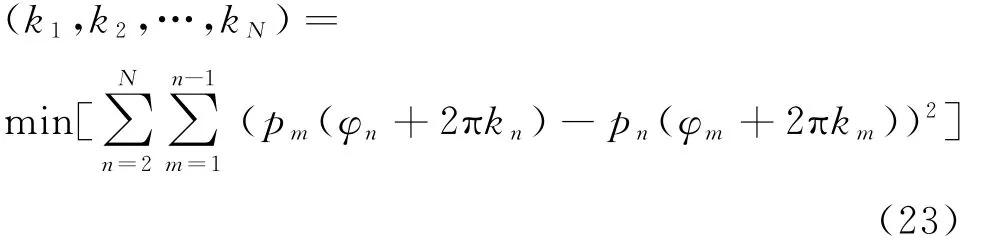
(k1,k2,…kN)组合方式共有,对于每种确定的(k1,k2,…kN),需要进行C2N项平方和运算,每个平方项需要5次乘法运算和3次加法运算。因此,对于每种确定的 (k1,k2,…,kN),需要进行(5 N(N-1)/2)次乘法运算和(2N2-2 N-1)次加法运算。因此,参差基线解模糊算法共计需次乘法运算、(2N2-2 N次加法运算以及次比较运算。

参差基线解模糊算法的计算量非常大,在多个基线的情况下,无法实时计算。

4.4 改进的解模糊算法复杂度

因此式(22)等价为:

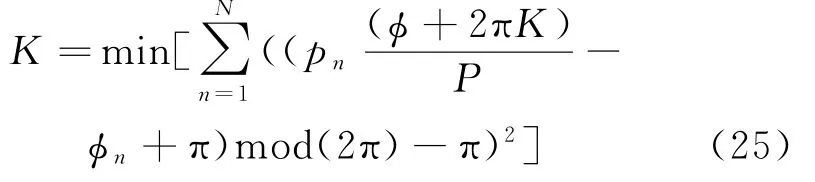
K取值范围满足式(20)。

改进的解模糊算法复杂度约为逐级解模糊算法复杂度的(5P/2)倍,远小于参差基线解模糊算法复杂度,该算法计算量较小,适合实时计算。

5 仿真实验

假设图1中相位干涉仪阵列由4个天线单元组成,信号频率为3 GHz,则可得λmin/2=50 mm,在满足基本基线长度d＜λmin/2的条件下,取d=40 mm,选取天线单元之间间距长度比值为2∶3∶5,则最长基线长度D=10 d=400 mm。

对于逐级解模糊算法,选取D1∶D2∶D3=1∶2∶10,其中D1为虚拟基线,而D3即为最长基线D。对于参差基线解模糊算法选取D1∶D2∶D3=2∶3∶5,即为天线单元之间间距长度比值,其基线比两两互质,符合参差基线解模糊算法要求。对于改进的解模糊算法,选取D1∶D2∶D3∶D=2∶3∶5∶10。

假设目标处于方位范围为±45°,测量相位误差εn～N(0,σ2)。取0≤σ≤60,以2°为步进。对于每个σ值,选取目标处于方位范围为±45°,以5°为步进,对每个方位进行10 000次蒙特卡罗实验,要求最大基线相位误差小于180°,即最大基线模糊数K计算正确时,算法结果正确。统计每个σ值各个方位的正确实验次数,除以实验总数,即为正确解模糊的统计概率,如图2所示。

由仿真结果可知,随着σ值增大,3种方法正确概率均下降明显,逐级解模糊算法正确概率明显小于参差基线解模糊算法以及改进的解模糊算法。参差基线解模糊算法正确概率最大,而改进的解模糊算法正确概率与参差基线解模糊算法相比差距较小。

图2 相位误差与解模糊概率的统计关系

6 结束语

本文基于参差基线解模糊算法原理,利用最长基线鉴相精度,提出了一种改进的解模糊算法,并与传统的逐级解模糊算法以及参差基线解模糊算法进行了比较。从算法复杂度分析,改进的解模糊算法复杂度大于逐级解模糊算法,远小于参差基线解模糊算法。从解模糊正确率的仿真结果分析,改进的解模糊算法正确概率与参差基线解模糊算法差距较小,明显高于逐级解模糊算法。因此,该算法兼具计算量小、适合实时计算以及正确概率高的优点,适合工程应用。