一种应用于特征识别的高分辨率功率谱设计与实现
2018-10-23赵荣琦
赵荣琦,王 飞,王 林
(中国船舶重工集团公司第七二三研究所,江苏 扬州225101)
0 引 言
由于电子对抗技术的不断进步,干扰与抗干扰之间的斗争日趋激烈。面对日益复杂的电子干扰环境,雷达必须提高其抗干扰能力才能在现代战争中生存,才能发挥其正常效能。雷达有源干扰的智能识别具有重要的军事战略意义,通常有源干扰类型识别是基于特征参数进行分析的[1],其基本流程如图1所示。
在识别干扰前需要分析各种典型干扰模式的产生机理,将不同类型的干扰信号在时域、频域上的特征进行归纳。在处理频域特征时,通过分析样本数据进行功率谱分析,估算出被分析对象的能量随频率分布的情况[2],为信号特征识别算法中信号的频域特征分析提供数据。为此,本文基于现场可编程门阵列,采用基4-FFT算法完成1 024点快速傅里叶变换,利用改进的周期图谱分析方法对1.28 GHz采样数据进行处理,完成了高分辨功率谱设计,为干扰噪声的特征识别提供频谱数据。
1 功率谱设计原理
1.1 周期图谱估计方法
功率谱作为采样数据在频域内统计特征的描述,在许多技术领域内有着广泛应用。信号的功率谱密度反映了信号的功率在频域随频率的分布。利用给定的N个样本数据估计一个平稳随机信号的功率谱密度叫做谱估计[3]。取平稳随机信号x(n)的有限个采样点x(0),x(1)...x(n),对采样数据直接进行傅里叶变换,进行谱估计得到功率谱:

由于序列x(n)的离散傅里叶变换(DFT)具有周期性,因此这种功率谱同样具有周期性,被称为周期谱。在实际工作中进行的观测必然是在有限范围内进行的,因此可用数据长度N来限制。同时,不同的观测数据所得的周期图也存在差异,由于这种随机起伏大,使得周期图不能得到相对稳定的估值。
为此,改进的周期图谱估计方法是先把分段的数据乘以窗函数进行加窗处理,分别计算其周期图,然后进行平均,将分段的谱估计结果的平均值作为最终的功率谱估计值:

式中:L为每段的数据长度,各段数据可以有部分交叠覆盖。
为了得到较好的功率谱估值,加窗和平均处理应当兼顾减小随机起伏和保证足够的谱分辨率这2个方面。同时,各段的数据可以认为是相互独立的,这样获得的谱估计的方差将减小到每段估计结果的1/M。
1.2 窗函数
数字信号处理中通常是取其有限的时间片段进行分析,信号的截断会产生能量泄漏,而用FFT算法计算频谱又会产生栅栏效应。在FFT分析中为了减少或消除频谱能量泄漏与栅栏效应,常采用不同的截取函数对信号进行截短,截短函数称为窗函数[4]。
能量泄漏与窗函数频谱的两侧旁瓣有关,窗函数的选用要从保持最大信息和消除旁瓣的综合效果出发来考虑,因此窗函数频谱中的主瓣宽度应尽量窄,旁瓣衰减应尽量大,但这2个要求通常无法被同时满足。图2对比了几种常用的窗函数对信号频谱特征的影响。

图2 窗函数特征对比
由图2可以看出,矩形窗函数有较大的旁瓣,并有负旁瓣,导致变换中带进了高频干扰和泄漏,因此常用在仅对主瓣频率精度有要求,而不考虑幅值精度的情况;布莱克曼窗主瓣宽,旁瓣小,频率识别精度低,幅值识别精度高,常用来检测2个频率相近、幅度不同的信号;汉宁窗旁瓣幅度小,常用来分析窄带信号;对于随时间按指数衰减的函数,可采用高斯窗。信号的加窗处理,重要的问题是在于根据信号的性质和研究目的来选用窗函数。
1.3 基-4FFT算法
FFT是在DFT基础上,根据DFT的奇偶、虚实特性对其进行改进的一种快速算法。1组有限长序列x(n)的离散傅里叶变换表示为:
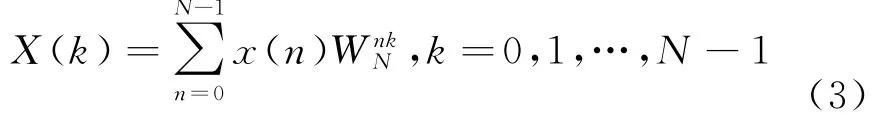
利用旋转因子的周期性、对称性、可约性,将式(3)中的x(n)分解成4个N/4点的序列,分别计算DFT可得:
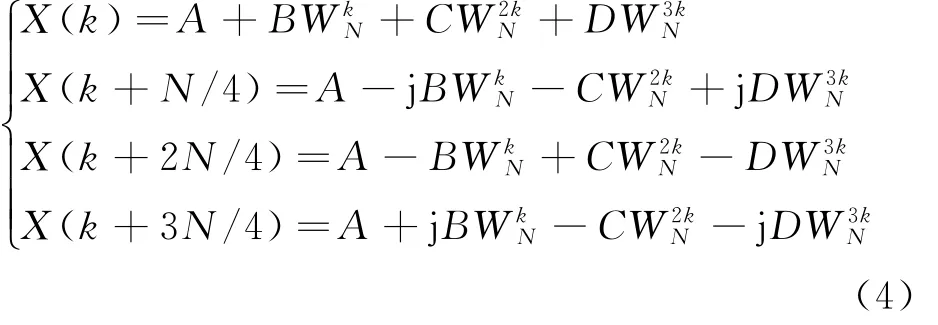
将式(4)进行多级分解后便可以通过4点的DFT逐层迭代完成整个运算,该方法称为蝶形运算[5],蝶形运算单元如图3所示。
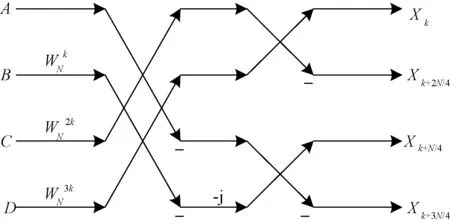
图3 基4蝶形运算单元结构图
2 高分辨率功率谱的实现方法
本文所设计的高分辨率功率谱具体实现流程是将1.28 GHz的连续采样数据进行加窗处理,将每段加窗后的数据作1 024点FFT运算,计算出1组数据的频谱信息,将多组连续数据的频谱取平均作为最终的功率谱。
2.1 窗函数设计
连续采样数据首选经过窗函数作加窗处理。在干扰信号识别的复杂信号环境中,如果信号中有许多远离被测频率的干扰频率分量,应选择旁瓣衰减速度较快的窗函数;如果干扰频率分量紧邻被测频率时,需选择旁瓣峰值较小的窗函数[6]。因此,本设计中选择旁瓣低且衰减快的窗函数。同时,窗函数频谱中旁瓣越小,使能量相对集中在主瓣,就可以较为接近真实的频谱[7]。参考文献[7]提出了一种旁瓣最低与最速下降(FDMS)窗函数的分析与设计方法,可以减少频谱泄露,提高对不同频率信号的提取能力。
FDMS窗是一类余弦组合窗,其时域表达式为:
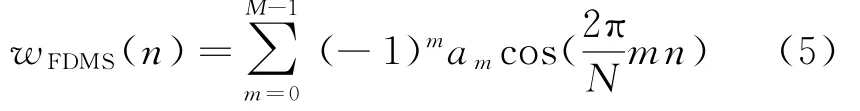
式中:M为窗函数的项数;n=1,2,…,N-1。
典型的FDMS窗函数和其他窗函数旁瓣性能对比见表1。

表1 窗函数性能比较
由表1可见,4项FDMS窗的旁瓣渐近衰减速率为18 dB/oct,旁瓣峰值电平达到了-93 dB,具有较理想的旁瓣特性,其中系数a1=0.355 768,a2=0.487 396,a3=0.144 232,a4=0.012 604[7]。将FDMS窗与常用窗函数中旁瓣较小的布莱克曼窗进行对比,结果如图4所示。在旁瓣衰减速率相同的情况下,FDMS窗的旁瓣峰值更小,能量更集中在主瓣。因此,本文采用4项FDMS窗对输入信号进行处理,旁瓣电平小且渐近衰减速率大的窗函数能抑制频谱泄漏的影响,提高频谱分析的准确度。生成1 024点窗函数系数后,在FFT运算前将每组采样数据与窗函数相乘,完成加窗操作[8]。

图4 FDMS窗与布莱克曼窗对比
2.2 FFT的硬件实现
1 024点FFT运算是实现高分辨率功率谱的关键环节。功率谱中1 024点FFT算法整体架构如图5所示,其中包括5级基-4蝶形运算。

图5 1 024点FFT算法整体架构
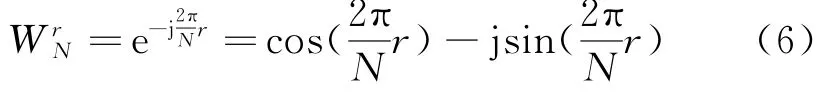
根据图3蝶形运算单元结构,每个运算单元需要3个复数乘法器和12个复数加法器,其中复数乘法运算如下:

根据式(7),一次复数乘法包括4次实数乘法和3次实数加法,将复数乘法作如下转换可减少其中实数乘法的数量:

根据公式(6),用Matlab预先计算出旋转因子的值,生成各级蝶形运算的旋转因子表,在程序执行时直接查表,节省时间,提高运算速度。本文对旋转因子的实虚部采用16位有符号数据存储,将旋转因子值扩大215,以便参与蝶形运算中的定点运算。
在每个蝶形运算单元中,旋转因子的值是固定不变的,因此将cosθ-sinθ、cosθ+sinθ的值存储于旋转因子ROM中,能够将每个复数乘法简化为3次实数乘法和4次实数加法,这将大大减少FPGA中逻辑资源的消耗。
3 实现结果验证
为验证该功率谱,本文对干扰模拟器发出的多种干扰信号进行了测试。设置中心频率320 MHz、带宽50 MHz的窄带噪声,通过本文设计的功率谱得到的频谱特性如图6所示。由图6可以看出,2条最大的谱线出现在320 MHz和960 MHz频率处,谱线宽为50 MHz,窄带噪声测试正确。中心频率320 MHz、带宽100 MHz的宽带噪声干扰信号的频谱特性测试结果如图7所示。相比于图6,宽带噪声的功率谱宽明显增加。
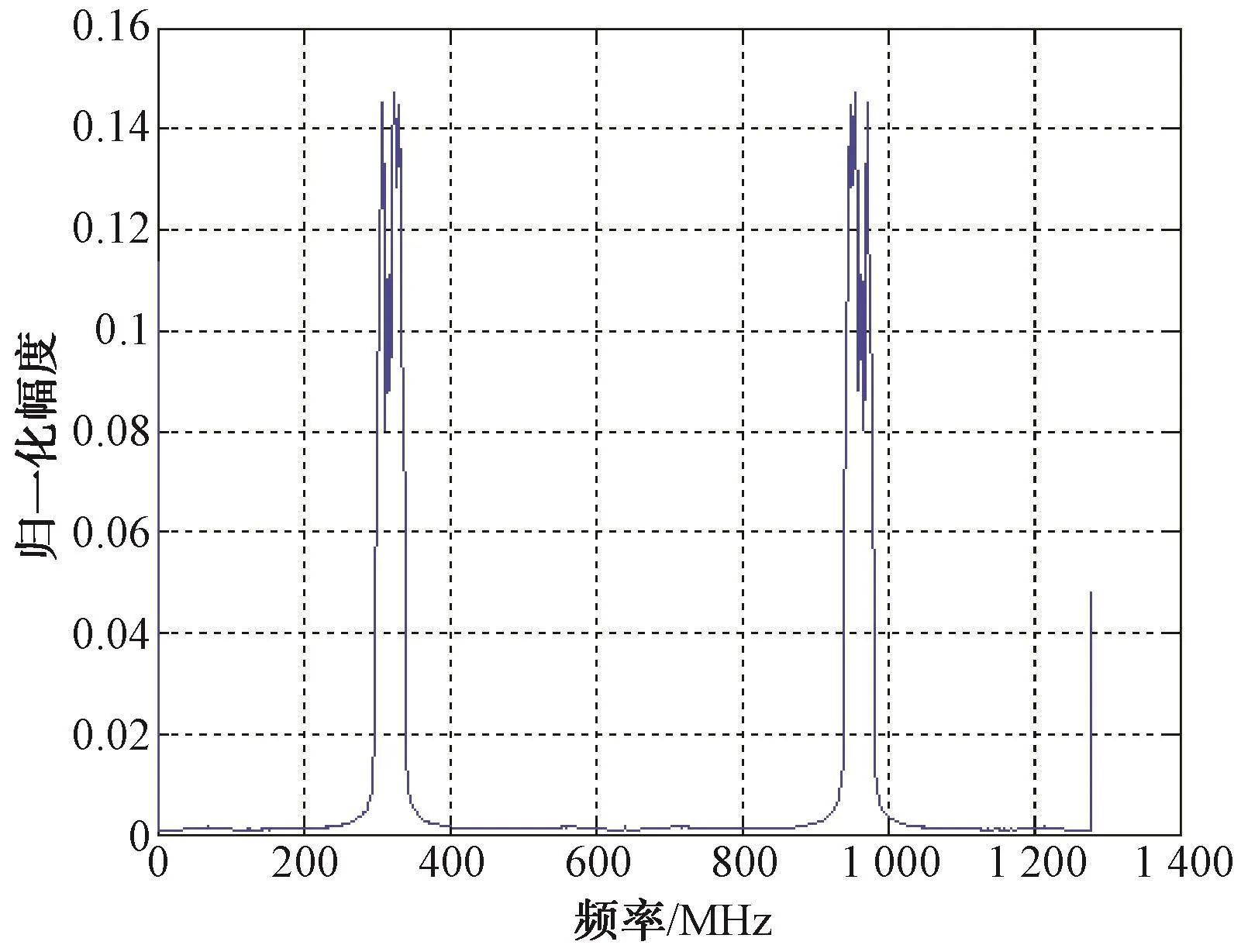
图6 窄带噪声阻塞干扰信号的功率谱
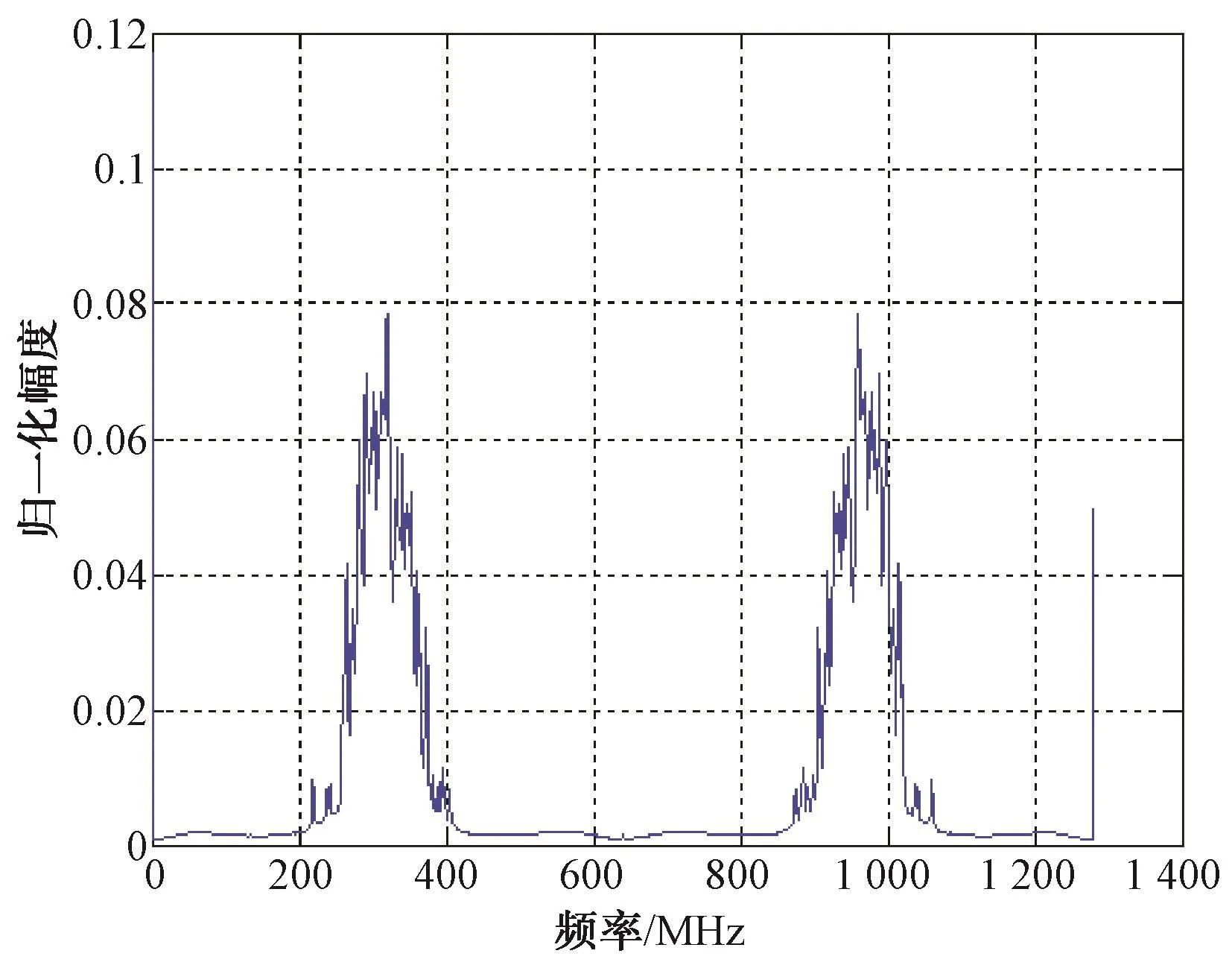
图7 宽带噪声阻塞干扰信号的功率谱
设置干扰信号为梳状谱噪声,测得的频谱特性如图8所示。图8有明显的蓝色梳状谱梳齿,可以分析出梳齿的数量、频率、宽度与间隔信息。

图8 梳状谱干扰信号的功率谱
测试结果表明,高分辨率功率谱的分析结果达到预期设计要求,能够为后续的干扰特征识别提供正确的频谱特征数据。
4 结束语
本文对功率谱的设计原理进行了分析,给出了有源干扰类型识别背景下,基于FPGA的高分辨率功率谱的设计与实现结果。结果表明该功率谱分析结果正确,能够为各类干扰信号特征的识别提供良好的频域特征数据。
