优化DBN在BLDCM控制中应用研究

李晶

（ 辽宁工程职业学院，辽宁 铁岭 112008 ）

0 引言

随着智能制造和工业4.0技术的兴起，工业制造、新能源等领域的设备日趋复杂化、智能化、精密化和综合化，运行工况和工作环境也愈加复杂多变，其维护和保障成本越来越高。由于设备组成环节和影响因素的增加，仅仅通过传统可靠性工程方法和手段，依托个人经验的人工诊断方法已逐渐无法适应设备的变化。研究面对复杂系统的基于智能数据驱动的故障诊断方法成为该方向的热点。

1 概述

深度学习作为机器学习领域的一种新兴方法，以其强大的自动特征提取能力在图像、语音识别等领域取得了辉煌的成果[17]，其本质就是通过数据驱动的方式从原始数据中学习一些特征，而不是利用人工设计特征提取器进行提取。常用的深度学习模型有深度置信网（Deep Belief Nets，DBNs）、卷积神经网络（Convolutional Neural Networks，CNN）和深度神经网络（DNN）[17]。图1给出了深度学习方法的算法体系结构。

图1 深度学习算法体系结构

AGV(Automation Guided Vehicles，自动导引车)又名智能机器人，是一种具有自动定位装置，在没有人工指挥的前提下，按照指定的路径行进，实现目标牵引、货物搬运及生产新装配等领域的特殊用途。对AGV进行精准的定位是动态跟踪的关键环节。[15]

AGV作为一种耦合性极强、高度非线性自动引导装置，在运行环境复杂多变的状态下，如何应对不断增长的信息量，提高信息采集的准确度和效率，对AGV定位提出了更高的要求。针对这一问题提出一种动态学习率策略训练RBM网络，该方法通过在训练过程中逐渐调整学习率，克服固定学习率存在特征提取精度不高的缺点，提高RBM和DBN的特征向量映射能力。将学习算法应用于AGV定位的实验中，实验结果表明准确度和及时性有明显提升。

2 深度信念网络(DBN)

深度信念网络(Deep Belief Networks，DBN)是一个概率生成模型，由多个受限玻尔兹曼机(Restricted Boltzmann Machine， RBM)堆叠和一层BP神经网络而成，深度信念网络的底层接收输入数据向量，通过RBM转换输入数据至隐含层，可视层和隐含层之间有双向链接权值。为尽可能保留更多的各特征空间特征向量信息，每一层RBM必须单独训练，且相同层级之间无信息沟通[18]，其基本结构如图2所示。DBN的核心即通过数据驱动的方式从原始数据中自动学习一些特征。整个DBN的特征提取能力主要取决于RBM的学习能力，RBM由一个可见层V和一个隐含层H组成。DBN网络拓扑结构如图3所示。

图2 RBM网络结构

图3 DBN网络结构

在DBN网络结构中每一层的RBM网络信息都实现正反向传播，即RBM网络可视层与隐含层之间实现信息共享从而达到对目标测试函数值进行调整，网络结构的最后是BP神经网络层接收最后一层RBM输出数据，它能最大范围的削弱BP神经网络容易陷入局部极小点和寻优过程过长的缺点[16]，BP的反向传播网络能够将某些需要调整的信息自回传给RBM，进而使整个DBN网络训练参数结果达到最优，已经证明在BP网络之前，整个网络寻优的效果已较好[3-4]，因此BP的作用是对整个DBN进行微调。

在DBN训练过程中，第一层网络接收原始数据的特征向量，之后沿DBN网络进行传递，每一层采集数据的一个或多个方面的特征，并把采集的特征信息作为下一层的输入。经过多次传输之后，在上层网络中形成更易分类的组合特征向量，因此DBN是一个含有多隐含层的深度架构的神经网络。文献[11]证明网络中RBM的个数有效提高了整个DBN网络的稳定性，且RBM个数越多，特征向量更加具体，用于数据分类的训练结果也更精确，但一般来讲使用2～3个RBM的结果已经足够精确[11]。

2.1 受限玻尔兹曼机（RBM）及改进

如图2所示，由于普通RBM前后层之间进行双向全链接，但同一层的不同单元之间没有链接，这也是RBM“受限”的原因。

RBM网络中，可视层的特征向量∂和隐含层的特征向量δ可由联合分布概率表示。

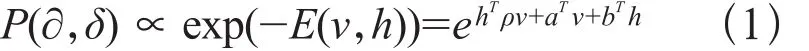
式中，ρ为可视层和隐含层之间的权值，E(∂，h)是特征向量∂和δ的数学期望值，其绝对值的大小代表h能够保存的∂的特征信息的多少。未获得最优特征值，需要求θ=(ρ，a，b)，使联合概率分布P(∂，δ)最大[12]。由于最大似然法不能求出满足条件的θ，为使P(∂，δ)达到最大，更新新权值：

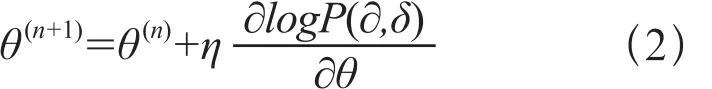
式中，n为迭代次数，η为学习速度。迭代次数在100＜n＜200时，学习速率η能够影响网络的学习进度，在0＜n＜100时，算法应以较大的η快速学习，迭代值在大范围内调整，接近输出时，网络基本趋于稳定，只需η微调技能得到最优特征值。因此，传统的固定长度的学习速率η不适用于全程迭代寻优，本文引进入一个学习参数μ以动态调整学习速率，改进后的学习率如下：

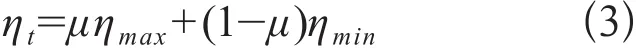
式中，μ为学习参数，用以调节学习率大小，ηmax和ηmin为预先设定的学习率上边界和下边界，η为n的倒数，因此可令ηmax和ηmin分别等于1/n和1/2n。

改进后的网络训练过程可由公式(3)计算得出：

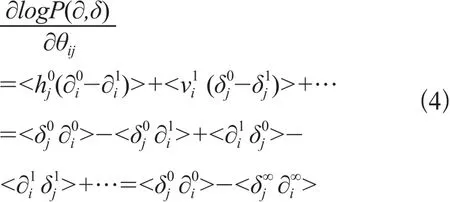
式中，＜δ0∂0＞为输入特征向量与其对应的隐含层特征向量的点乘的平均值，＜δ∞∂∞＞为MCMC末端可视层特征向量与其对应的隐含层特征向量的乘积的均值，＜δ∞∂∞＞是收敛的[17]。由公式(4)可知，联合概率分布的斜率与中间状态无关，只与网络的初始状态和最终状态有关，根据公式(3)可得修改后的参数θ，从而达到训练的目的。权值更新公式为：

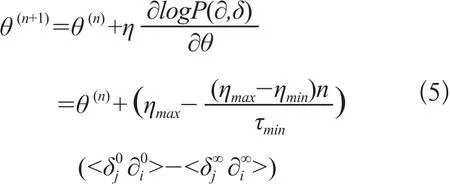
2.2 BP网络的调整过程

BP网络在DBN中实现有约束分类的作用，其接收最后一层RBM的输出特征向量，并对数据进行分类，起到微调DBN的作用[15]。其训练过程主要分为两步：第1步是前向传播，将输入特征向量沿输入端传播至输出端；第2步是反向传播，将BP网络的输出结果与带有约束条件的正确结果相比得到误差，然后将误差从反向传播至输入端，以修改DBN的参数[16]。本文实验中利用sigmod函数作为BP的网络节点的求值函数，具体实现步骤如下。

①初始化网络的参数，设定步长B；

②进行正向计算，对于第l层的j单元节点，有

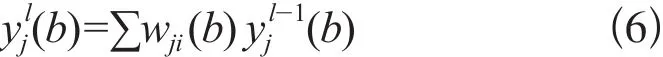
若该神经元属于输出层(l=L)，则令yjl(b)=Oj(b)，误差ej(b)=dj(b)-Oj(b)，其中dj为带约束条件的正确信息；

③计算φ，将其反向传递用来修正网络的权值参数，对于输出单元有：

对于隐含层单元有

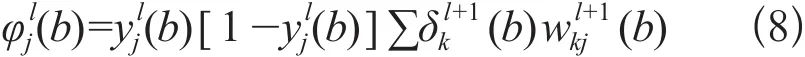
④修改权值：

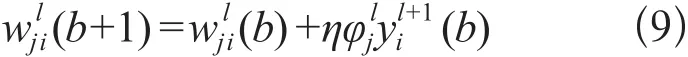
η为学习速率；

⑤如b=B，则训练结束，反之，b=b+1，返回步骤②。

3 实验与分析

Galil控制数控机床中的无刷直流电机控制系统如图4所示，控制器由改进型DBN神经网络、数模转换器和零阶保持器三部分组成，AMP是PWM驱动电路产生的作用于无刷直流电机的误差放大装置。给定相关参数，即可得到无刷电机控制系统闭环传递函数，通过PID调节信号，使闭环系统得到较理想的输入函数，从而使整个电机控制系统的输出达到理想的状态。DAC是采用16位寄存器用来实现数字量向模拟量的转变，ZOH零阶保持器周期取决与控制器的采样周期T。图中各组成部分的相应函数及变量如下所示：

图4 PID控制系统方框图

零阶保持器的传递函数为

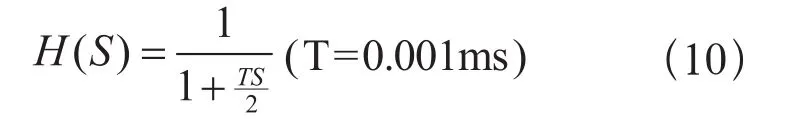
DAC输出模拟电压范围V

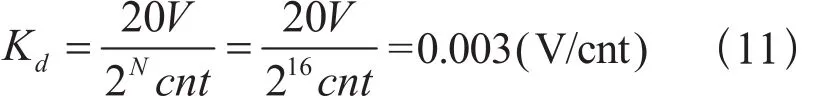
AMP

Motor& Encoder由编码器和电机两部分组成的，编码器的参数为

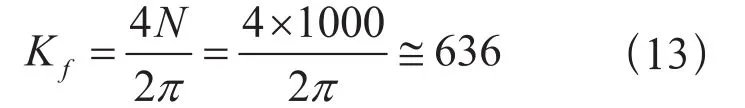
无刷直流电机数学模型得：

电阻Ra为2.58Ω，转子惯量J=1.30E-04，转矩系数Kt为0.208粘性阻尼B为3.78E-03。

设定参数根据相互间的关系列出各环节传递函数。运行程序得到系统闭环传递函数

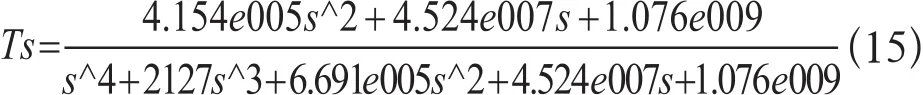
得到相应节约响应曲线见图5。

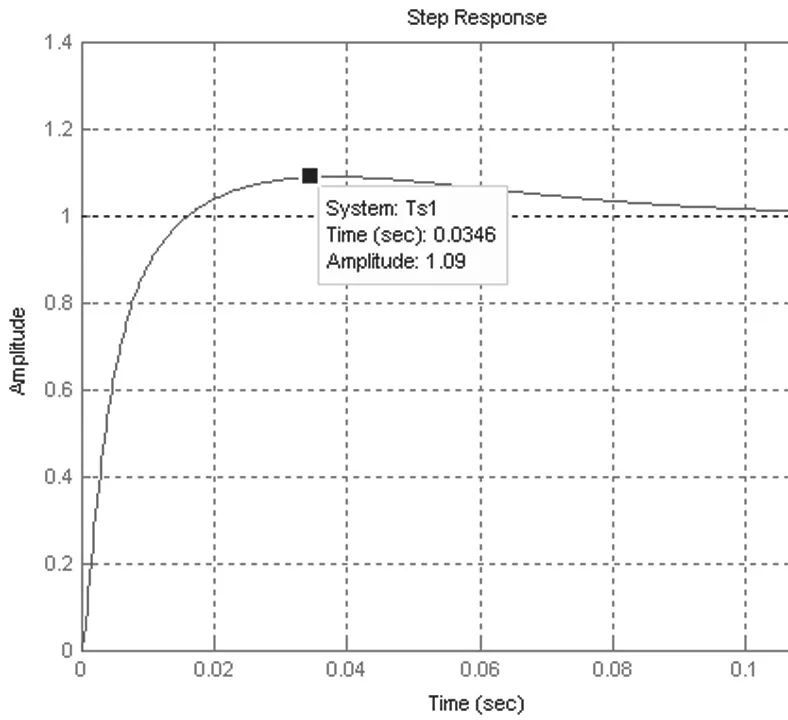
图5 PID控制器调节下无刷直流电机控制系统阶跃相应图

实验步骤为：首先，建立一个含有两层RBM的DBN网络，每个RBM含有100个神经元，用2000个输入(包括R(s)， Y(s))输出(Y(s+1))数据训练RBM，迭代次数为50，其中学习速率为0.01～0.02，用BP算法对网络进行微调，迭代次数为50，学习速率为0.01～0.02，最后用训练好的DBN对1000个测试组(包括R(s)， Y(s))进行控制预测。

表1为实验结果比较。

表1 实验结果比较

通过上述实验可见，改进方法的神经网络较原始网络在响应时间有所加快，通过使用两层RBM的叠加，DBN的训练精度有较为明显提升，证明了改进神经网络的有效性。

4 结语

本文论述了深度信念网络(DBN)的兴起和发展，介绍了网络结构和算法并分析了算法的优越性，针对算法的固定学习率引起的寻找最优值准确度不高的问题进行了改进，并修改输出层函数使网络应用于无刷电机系统的控制实验中，实验结果表明改进策略能够有效提高系统响应时间，提高准确性。此外，该改进型DBN可以应用于在图像处理、模式分类，自动控制等任务中，是较理想适用于控制领域的算法。