运用案例教学渗透数学思想方法初探

文/广州市从化区鳌头镇车头小学 贾玉英

一、案例教学与数学思想方法的概述

本文所指的 “案例”,指的是在小学语数英的一节课中,教师围绕单元或课文的训练重点选择帮助学生在学习时突破这个训练重点的例子或一组材料，这个例子必须真实,在某一类中具有典型性，能给学生带来一定的启示和体会，能举一反三帮助学生解决问题。 “案例教学”是在教师指导下，根据一定的教学目的，选择带有启发性的典型案例，通过师生之间、生生之间的多向互动、平等对话和积极研讨等形式，引导学生阅读、思考、分析、讨论、表达和交流、让学生感悟、理解和掌握知识，培养学生分析问题和解决问题等核心素养，使学生学会自主、合作、探究式学习的一种教学方法。

数学思想方法的渗透是数学核心素养中的“自主发展——学会学习——乐学善学”的范涛。数学思想方法是数学中的理性认识，是数学知识的本质，是数学中高度抽象、概括的内容，它蕴涵于运用数学方法分析、处理和解决数学问题的过程之中。 《义务教育数学课程标准 (2011年版)》:数学思想方法的教学具有极其重要的意义。

案例教学很早就应用于其他领域的教学中，但在数学教学中运用甚少。本文尝试从运用案例教学在小学数学课堂中渗透数学思想方法这一个层面来培养学生的核心素养进行探索。

一、运用案例教学渗透模型思想

数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构。 “模型思想”是义务教育数学课程标准 （2011年版）提出的十个核心概念之一，具有重要的数学价值和教育价值。由于模型思想非常重要，所以我在教学实践中重视根据相关的教学内容运用案例教学渗透这种数学思想方法。下面以 《乘法分配律》为例，谈谈运用案例教学法渗透模型思想。

《乘法分配律》在小学计算中起到重要的作用，但小学生常会出错，在教学 《乘法分配律》之前，我认真研读教参，发现里面有一句话： “运算定律的学习为学生从原理上理解不同的关系提供了可能。比如分配律的学习中，无论从 （a＋b）×c=a×c＋b×c 的分解式思考， 还是从 a×c＋b×c=（a＋b）×c 的合并式思考，都可以结合乘法的意义来理解。”我设计了案例教学视频，视频内容如下：一位小男孩到商店为同学们买故事书。故事书每本25元，他先挑了4本，后来又挑了2本，一并付了150元。这时，又进来一位小女孩买同样的故事书，她先挑了4本，付了100元，后来又挑了2本，再付50元。她一共付了150元。

由这个案例引发学生思考：书的单价与他们买的书的本数一样么？他们付钱的方法有什么不同？他们付的钱相等么？请你用算式分别表示他们付的钱。学生列出的式子有如下可能：

小男孩付的钱 小女孩付的钱

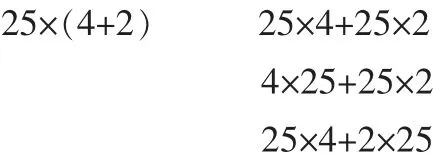
通过引导学生观察思考，学生得出了 （4＋2）×25=4×25＋2×25。 我引导学生根据乘法交换律理解左边的每一道式子都等于右边的四道式子。再引导学生从乘法的意义上理解：6个25等于4个25加2个25，从而引导学生得出了乘法分配律的定义：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。 左边小男孩用的是合并式思考方法，右边小女孩用的是分解式的思考方法。 接着，引导学生用字母表示这个模型：分解式：（a＋b）×c=a×c＋b×c， 合并式： a×c＋b×c=（a＋b）×c。 这样， 运用案例教学法让学生建立了乘法分配律的模型，培养学生的建模意识和用模的意识，渗透模型思想与分类思想。

建立了模型，还要用模，将相关的练习题归类看是否属于这个模型，能否用这个模型进行简便运算。在练习过程中，我要求学生根据式子的特点灵活选择分解式或合并式的思考方法，例如，我设计了以下练习：

在 （）里填上一个数，在○里填运算符号，使式子能运用乘法分配律进行简便运算。

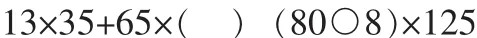
此题加深了学生对乘法分配律的模型的特点的理解，评讲后再让学生择优选用最佳的答案，再应用模型进行计算。

二、运用案例教学渗透数形结合思想

数形结合，指的是数与形之间的一一对应。通过”以数解形”或“以形助数”，即通过抽象思维与形象思维相结合，使抽象问题具体化，复杂问题简单化，从而优化解题途径。 数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休。”可见数形结合的数学思想十分重要。

通过深入研读教材，我认为《乘法分配律》的教学还可以运用案例教学法渗透数形结合的思想。

我设计了一个案例，以微课的形式呈现这个现实生活的情景的案例： “小红家的果园由连在一起的一块长方形的荔枝林和一块长方形的龙眼林组成， （可画出如下示意图），小红家的果园有多大？”通过呈现这个现实生活中的数学案例，引导学生独立思考。

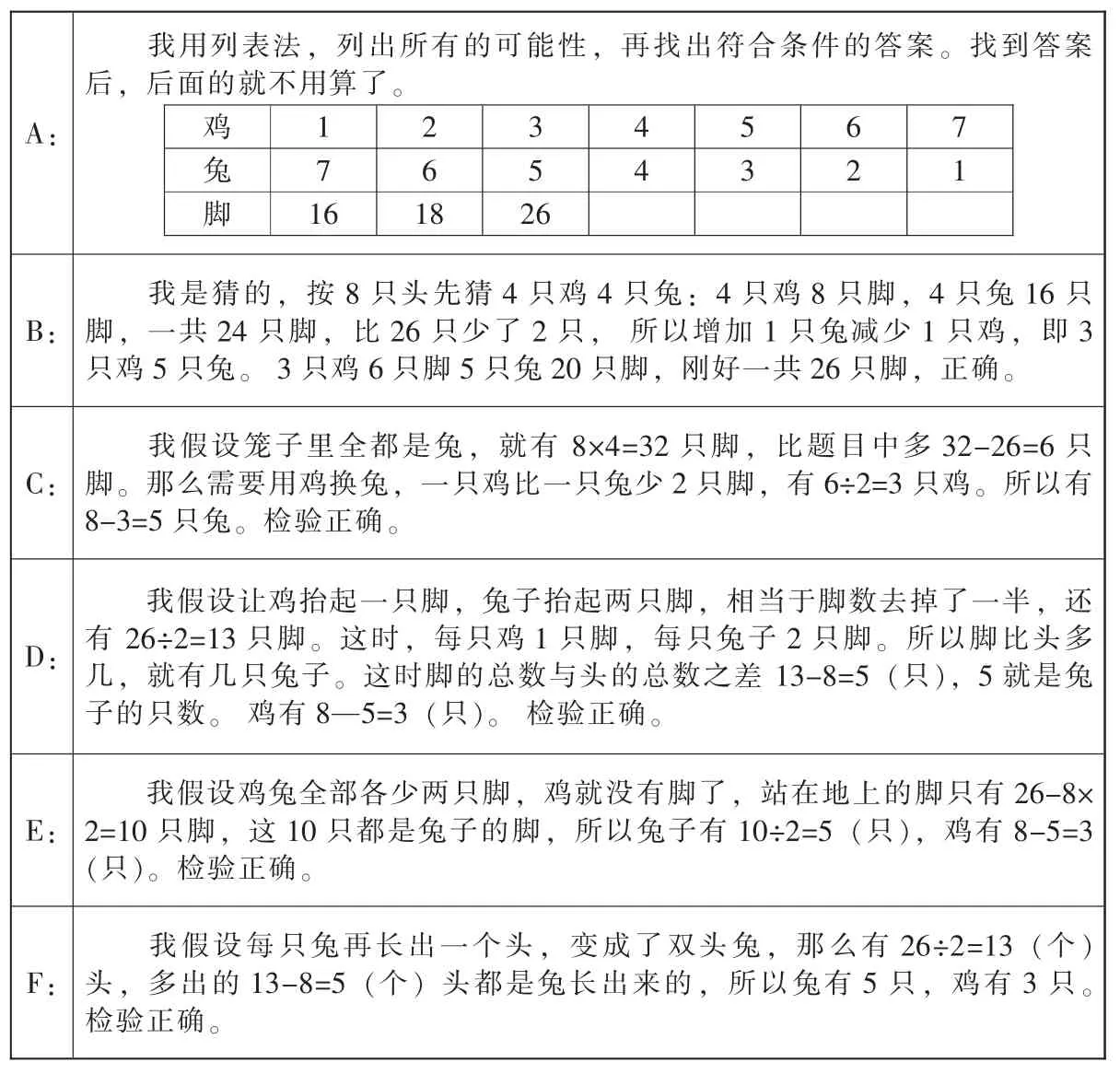
表1

学生列出：(33+67)×22和 33×22+67×22

第一种是合并式思考的方法，求100个22是多少。第二种用了分解式思考，33个22加上67个22是多少。学生完成后问：哪种方法较好？

这样，运用案例教学法，结合解决实际问题的过程，理解乘法分配律的含义，培养解决生活中相关实际问题的能力，渗透了数形结合思想和多样化择优的思想。

三、运用案例教学渗透转化思想

转化的数学思想方法将某些已知条件或数量关系转化为另外的条件或关系,化新知为旧知、化繁为简、化难为易的一种数学思想方法。相对其他教学法而言，运用案例教学法渗透转化的数学思想方法则别有新意。下面以 《鸡兔同笼》为例，探讨如何运用案例教学渗透转化的数学思想方法。

人教版新教材四年级下册的“数学广角”内容中出现的鸡兔同笼问题难度降低：笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各几只？

为了使学生很好地理解，我用动画设计了微课形式的教学案例，在学生独立思考并讨论后，播放《鸡兔同笼》案例。先呈现鸡兔同笼的题目动画形象与问题：笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各几只？ 几个小朋友 (以下分别用ABCDEF代替)围在旁边，各自思考，各抒已见。 （见表1）

在这个案例的各位孩子的讨论中，无论哪一种假设法都是用了不同形式的转化，巧妙的转化还显示了其解法的优越性，而这些转化均体现了同一种数学思想——化归思想，还渗透了对应思想与变中抓不变的思想方法。通过转化，灵活地解决了问题。这个案例数据简单，呈现形式生活化；通过重视双边互动教学，在学生独立思考后再播放呈现，避免了学生不思考直接等答案，培养了学生独立思考的能力。运用这个案例，再解决1500年前《孙子算经》中： “今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里，从上而数，有35个头;从下而数，有94只脚。求笼中各有几只鸡和兔?”此类数据较大的题目就得心应手；学生也能举一反三，解决其他相关的问题也水到渠成。