因式分解教学中如何培养学生的思维能力
2018-10-22兴宁市宁塘中学张伟锋
文 兴宁市宁塘中学 张伟锋
因式分解是初等代数恒等变形的重要内容和方法之一,历来是初中数学的难点。如何突破这一教学难点?
一、运用类比思想,训练思维的逆向性
中学数学利用类比产生新知识新方法的内容有很多,教学中应注意启发、引导学生在知识的形成过程中学习类比,在解决问题的实践中学会类比,从而训练思维的逆向性。
“因式分解”的前一章是 “整式乘除”,教材由整式的乘法很自然地引入因式分解。

把①式反过来写,就是
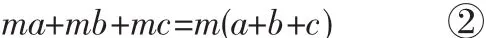
①式是做整式乘法,②式是进行因式分解。由此可以看出,因式分解正好与整式乘法相反。
这里明确地指明了因式分解与整式乘法的关系,如果把乘法公式反过来,就可以用来把某些多项式分解因式。
紧接着把乘法公式(a+b)(a-b)=a2-b2,反过来,就得到a2-b2=(a+b)(a-b)等。
因此可以说,运用类比思想,抓住因式分解与整式乘法的互逆性这条主线是本章的教学关键,这既能使学生真正理解因式分解的含义,又可以从思维的角度训练其思维的逆向性。
二、进行自我纠正,强化思维的批判性
初一学生解题,往往经常出现错误,特别是正负号、括号之类。刚进入初二时学生的这种马虎习惯也不可能一下子全部改掉。教学中应引导学生在纠正错误的过程中透过表面现象,抓住问题的本质,多角度、多层次地研究、解决问题。
因此在教学中,我一开始就特别强调让学生运用因式分解与整式乘法的互逆关系来进行验算。教材上也十分注重这一点, 例如把3x2-6xy+x分解因式,学生往往提取公因式后,误写成3x2-6xy+x=x(3x-6y)。教材中特别提出: “注意x(3x-6y+1)=3x2-6xy+x, 而 x(3x-6y)=3x2-6xy, 所以原式分解因式为3x2-6xy+x=x(3x-6y+1), 而不是 3x2-6xy+x=x(3x-6y)。”为了加深学生的印象,我还教给学生一句口诀 “整项全提走,留1来看守”。通过验算,这样一来学生既养成了自我纠错的习惯,又大大地降低了出错率。
教材最后指出 “分解因式,必须进行到每一个多项式因式都不能再分解为止。”这是因式分解的一个难点。因为何时已止,何时未止,没有一个 “判别公式”,学生常是 “跟着感觉走”,因此常出现诸如:
m4-16=(m2+4)(m2-4)
x3-3x+2=(x-1)(x2+x-2)的 “未止”现象。
因此,在教学中,应要求学生对每一个多项式因式按 “①是否可提公因式;②是否可以套公式;③是否可用十字相乘法分解;④是否可以用分组分解法”的程序来进行鉴别,最后检查到每一个因式都不能再分解了,才可以肯定得 “原式分解因式的最后结果。”
三、提高观察能力,培养思维的敏捷性
因式分解中的难 “度”及灵活“度”,莫过于分组分解法。正如教材中所说 “用分组分解法时,一定要想想分组后能否继续进行,完成因式分解,由此合理选择分组的方法。”这里提出了 “合理分组”的问题,即分组时不能只考虑到这一步,还要考虑到下一步 “能否继续进行”。不能只考虑局部是否可提公因式,是否可套公式,而且还要考虑到全局,是否能 “完成因式分解”。这就需要提高学生的整体观察能力,培养他们思维的敏捷性。
例如把x2-6x-y2+9分解因式。
分析:若把x2-y2作为一组,因为x2-y2=(x-y)(x+y)剩下的-6x+9作为一组,得-6x+9=-3(2x-3)
则下一步就没戏了,而应该先通过整体观察发现x2-6x+9作为一组,下一步就可用应用平方差公式了,即
x2-6x-y2+9=(x2-6x+9)-y2=(x-3)2-y2=(x+y-3)(x-y-3),从而完成了因式分解。
通过一定的训练,学生的观察能力有较明显的提高。
四、鼓励钻研探索,培养思维的发散性
众所周知,因式分解无论看似简单的十字相乘法还是分组分解法,往往不是一蹴而就的。正如教材中所强调的: “必须注意,分解因数及十字相乘都有多种可能情况,所以往往要经过多次尝试。”这种 “多次尝试”就意味着探索和钻研。在教学中我告诉学生,科学需要顽强的钻研精神和不畏艰险的探索精神,而探索的艰辛又总是和成功的喜悦相伴并存的,让他们通过自己的钻研去亲身体会成功的喜悦,以提高他们的钻研精神和学习兴趣。
